НОУ ИНТУИТ | Элементы финансовой математики. Лекция 6: Финансовые ренты

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 24.09.2017 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 33 студентам

| Поделиться |

Поддержать программу

6.3.2 Ренты с начислением процентов m раз в год

Годовая рента

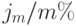В этом случае платеж R выполняется в конце каждого года, а проценты начисляются m раз в год по ставке $j_{m}$ , то есть каждый раз начисляется $j_{m}/m\%$ . Изобразим такую ренту на оси времени:

Вычислим наращенную к моменту n сумму этой ренты.

Последний платеж входит в наращенную сумму без изменения. Предпоследний платеж делается за 1 год до момента n, и на него начисляются сложные проценты m раз по ставке $j_{m}$ , то есть наращенная на этот платеж сумма в момент n будет равна

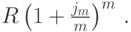
$R\left(1+\frac{j_m}{m}\right)^m\,.$

Третий от конца платеж делается за 2 года до момента n, и наращенная на этот платеж сумма в момент n будет равна 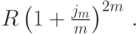$R\left(1+\frac{j_m}{m}\right)^{2m}\,.$ Первый платеж делается за n-1 год до момента n, следовательно, в момент n наращенная на него сумма будет равна

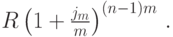
$R\left(1+\frac{j_m}{m}\right)^{(n-1)m}\,.$

Для вычисления наращенной суммы платежей мы применяли формулу из лекции 3. Наращенная сумма ренты состоит из наращенных сумм платежей:

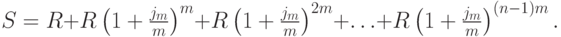
$S=R+R\left(1+{j_{m}\over m}\right)^{m}+R\left(1+{j_{m}\over m}\right)^{2m} +\ldots+R\left(1+{j_{m}\over m}\right)^{(n-1)m}.$

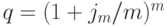Слагаемые этой суммы являются членами геометрической прогрессии с первым членом $b_{1}=R$ , знаменателем $q=(1+j_{m}/m)^{m}$ и числом членов k=n. Применим формулу (6.3) и получим:

$S=\frac{b_{1}(q^{n}-1)}{q-1}=% \frac{R\left[{\left(\left(1+{j_{m}\over m}\right)^{m}\right)}^{n}-1\right]}% {\left(1+{j_{m}\over m}\right)^{m}-1}=% R\,\frac{\left(1+{j_{m}\over m}\right)^{mn}-1}% {\left(1+{j_{m}\over m}\right)^{m}-1}$

Разделив числитель и знаменатель последней дроби на 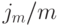$j_{m}/m$ и применив обозначение из формулы (6.4), получим:

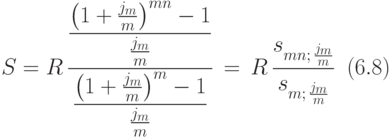
${\displaystyle S=R\,\frac{{\displaystyle\frac{\left(1+\frac{j_m}{m}\right)^{mn}-1}{\frac{j_m}{m}}}}% {{\displaystyle\frac{\left(1+\frac{j_{m}}{m}\right)^{m}-1}{\frac{j_{m}}{m}}}} \,=\,R\,\frac{s_{mn;\,\frac{j_{m}}{m}}}{s_{m;\,\frac{j_{m}}{m}}}\,\,\, (6.8)}$

Рассмотрим пример на вычисление наращенной суммы ренты по формуле (6.8). Он отличается от примера 54 только тем, что банк начисляет проценты 4 раза в год.

Пример 57. Фирма для создания фонда помощи ветеранам труда вкладывает в конце каждого года по 250 000 руб. в банк, выплачивающий проценты по ставке $j_{4}=8\%$ . Какая сумма будет на счёте фонда через 5 лет?

Решение. Вклады в банк образуют ренту, для которой R=250 000 руб., m=4, 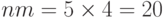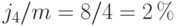$nm=5\times4=20$ , $j_{4}/m=8/4=2\,\%$ . Вычисляем наращенную сумму ренты по формуле (6.8), подставляя в нее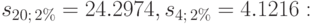 $s_{20;\,2\%}=24.2974, s_{4;\,2\%}=4.1216 :$

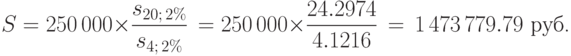
$S=250\,000\times \displaystyle\frac {s_{20;\,2\%}}{s_{4;\,2\%}}\, =250\,000\times \frac {24.2974}{4.1216}\,=\, 1\,473\,779.79\mbox{ руб.}$

Сравнивая ответ, полученный в примере 57, с ответом примера 54, находим, что начисление банком процентов 4 раза в год привело к увеличению наращенной суммы ренты на 7 129.54 руб.

p-срочная рента

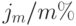В этом случае платежи производятся p раз каждый год через равные промежутки времени. Каждый платеж равен R/p. Проценты начисляются mраз в год по ставке j_m , то есть процент за один период равен $j_m/m\%$ . На оси времени эту ренту можно изобразить так же, как в п. 6.3.1. Найдем наращенную сумму этой ренты в момент n.

На последний платеж проценты не начисляются, и он входит в наращенную сумму без изменения, то есть в размере R/p. На предпоследний платеж начисляются проценты по ставке $j_{m}$ за период, равный 1/p части года, и наращенная к моменту n на этот платеж сумма равна

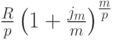
$\frac Rp\left(1+\frac{j_{m}}m\right)^{\frac mp}$

На второй с конца платеж начисляются проценты по ставке $j_{m}$ за период, равный 2/p части года, и наращенная к моменту n на этот платеж сумма равна

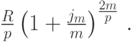
$\frac Rp\left(1+\frac{j_{m}}m\right)^{\frac {2m}p}\,.$

Последний платеж делается за 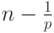$n-{1\over p}$ лет до момента n, то есть наращенная в момент n на этот платеж сумма равна:

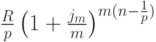
$\frac Rp\left(1+\frac{j_{m}}m\right)^{m(n-\frac 1p)}$

Вся наращенная на ренту сумма равна:

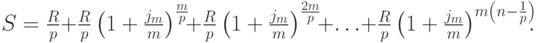
$S=\frac{R}{p}+\frac{R}{p}\left(1+{j_{m}\over m}\right)^{{m\over p}}\!+ \frac{R}{p}\left(1+{j_{m}\over m}\right)^{{2m\over p}}\!+ \ldots+\frac{R}{p}\left(1+{j_{m}\over m}\right)^{m\left(n-{1\over p}\right)}% \!\!\!.$

Слагаемые этой суммы являются членами геометрической прогрессии с первым членом 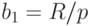$b_{1}=R/p\,$ , знаменателем

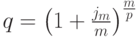
$q=\left(1+\frac{j_{m}}m\right)^{\frac mp}$

и числом членов k=np. Эта сумма равна:

$\begin{eqnarray*} S = \frac{b_{1}(q^{k}-1)}{q-1}=\frac{R}{p}\times \frac{{\left(\left(1+{j_{m}\over m}\right)^{{m\over p}}\right)}^{np}-1}% {\left(1+{j_{m}\over m}\right)^{{m\over p}}-1}=\\[4pt] = \frac{R}{p}\times\frac{\left(1+{j_{m}\over m}\right)^{mn}-1}% {\left(1+{j_{m}\over m}\right)^{{m\over p}}-1} \end{eqnarray*}$

Разделив числитель и знаменатель последней дроби на 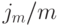$j_{m}/m$ , получим формулы:

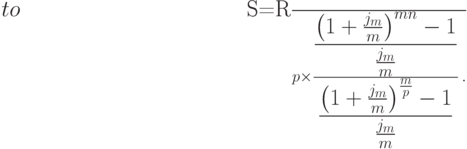
$\begin{eqnarray} S=\frac{R}{p}% \times \frac{{\displaystyle\frac{\left(1+\frac{j_m}{m}\right)^{mn}-1}{\frac{j_m}{m}}}}% {{\displaystyle\frac{\left(1+\frac{j_{m}}{m}\right)^{\frac mp}-1}{\frac{j_{m}}{m}}}} \,.\nonumber \end{eqnarray}$

Заметим, что функция 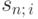$s_{n;\,i}$ была определена при выводе формулы (6.2) только для целых значений n (n - число членов ренты). Так как значения m/p могут быть нецелыми, будем считать теперь, что эта функция определена при любых положительных значениях n. Теперь мы можем переписать последнее равенство в более компактном виде:

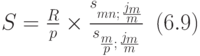
$S=\frac{R}{p}\times \frac{s_{mn;\,{j_{m}\over m}}}{s_{{m\over p};\,{j_{m}\over m}}}}\,\,\, (6.9)$

Рассмотрим пример на вычисление наращенной суммы ренты по формуле (6.9). Он отличается от примера 57 только тем, что годовая сумма денег, которую фирма кладет на счет в банк, разбивается на два равных платежа.

Пример 58. Фирма для создания фонда помощи ветеранам труда вкладывает два раза в год по 125 000 руб. в банк, выплачивающий проценты по ставке $j_{4}=8\%$ . Какая сумма будет на счете фонда через 5 лет?

Решение. Вклады в банк образуют ренту, для которой R=250 000 руб. , m=4, 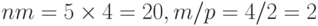$nm=5\times4=20, m/p=4/2=2$ ,

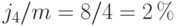
$j_{4}/m=8/4=2\,\%$

Вычисляем наращенную сумму ренты по формуле (6.9), подставляя в нее 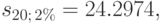$s_{20;\,2\%}=24.2974,$

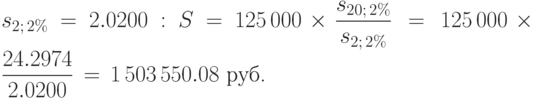
$s_{2;\,2\%}=2.0200: S=125\,000\times \displaystyle\frac {s_{20;\,2\%}}{s_{2;\,2\%}}\,=\, 125\,000\times \frac {24.2974}{2.0200}\,=\, 1\,503\,550.08\mbox{ руб.}$

Сравнивая ответ, полученный в примере 58, с ответом примера 57, находим, что разбиение годовой суммы на два равных платежа привело к увеличению наращенной суммы ренты на 29 770.29 руб.

В учебнике [5] рассмотрен также частный случай p-срочной ренты при p=m. В этом случае формула (6.9) может быть упрощена и принимает вид:

$S=\frac{R}{m}\, s_{mn;\,{j_{m}\over m}}\,\,\, (6.10)$

В финансовых моделях используются также ренты с непрерывным начислением процентов - годовые, p-срочные и с периодом больше года. Формулы для наращенных сумм таких рент похожи для уже рассмотренных в этой лекции. В случае годовой ренты имеет место формула:

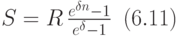
$S=R\,\frac{e^{\delta n}-1}{e^{\delta}-1}\,\,\, (6.11)$

а для p-срочной ренты имеет место формула:

$S=\frac{R}{p}\times\frac{e^{\delta n}-1}{e^{\frac{\delta}{p}}-1}\,\,\, (6.12)$

Дальше >>

Элементы финансовой математики

Элементы финансовой математики

Финансовые ренты

6.3.2 Ренты с начислением процентов m раз в год

Годовая рента

p-срочная рента

Вопросы и ответы

Студенты

Авторизоваться

Элементы финансовой математики

Элементы финансовой математики

Финансовые ренты

6.3.2 Ренты с начислением процентов m раз в год

Годовая рента

p-срочная рента

Вопросы и ответы

Студенты