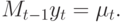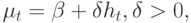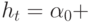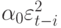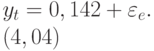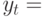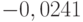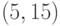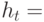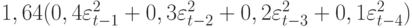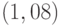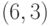Временные ряды с высокой изменчивостью

11.3. Модели АРУГ-М

АРУГ-модель обобщили Р. Энгл, Д. Лилиен и Р. Робинс, позволив среднему процесса зависеть от собственной условной дисперсии. Модели этого класса, названные АРУГ-М-моделями, удобны для изучения рынка ценных бумаг. Основная мысль состоит в том, что избегающие риска агенты (участники рынка) будут требовать компенсацию за то, что держат в своем портфеле рискованные ценные бумаги. Известно, что степень риска часто измеряется дисперсией доходности, поэтому премия за риск будет возрастающей функцией условной дисперсии доходности. Энгл и его соавторы выразили эту мысль, выписав превышение доходности y_{t} от держания рискованных ценных бумаг над государственными облигациями, рассчитанными на погашение в течение одного периода времени, принятого за единицу, в виде

(11.22)

где

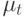	-	премия за риск, побуждающая избегающих риска агентов держать долгосрочные ценные бумаги, а не краткосрочные государственные облигации;
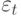	-	непредсказуемые колебания показателей доходности долговременных рискованных ценных бумаг.

Заметим, что ожидаемое превышение доходности от держания долгосрочных ценных бумаг должно быть равно премии за риск

(11.23)

Энгл, Лилиен и Робинс предполагали, что премия за риск является возрастающей функцией условной дисперсии 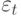; другими словами, чем больше условная дисперсия доходностей, тем большая компенсация необходима участнику рынка, чтобы продолжать держать долгосрочные ценные бумаги. Математически это означает, что

(11.24)

где

-

условная дисперсия .

Выразим 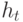как АРУГ-процесс

. (11.25)

Уравнения (11.22)-(11.25) образуют основу АРУГ-М-модели.

Если рассмотреть случай 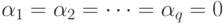, то модель АРУГ-М вырождается в хорошо известную модель с постоянной премией за риск. Как и в предыдущих случаях, принятие модели АРУГ-М может быть осуществлено на основании теста, использующего выражение типа (11.21). Статистика асимптотически распределена как 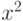с числом степеней свободы равным числу ограничений.

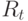-квартальная доходность трехмесячных облигаций за период от до . В конце двух кварталов, вложив один доллар, инвестор получит долларов. Пусть означает квартальную доходность от шестимесячных облигаций. Тогда 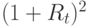- доход, полученный держателем шестимесячной облигации в конце срока хранения. Превышение дохода от держания шестимесячной облигации (без учета квадратичных членов) приблизительно составит:

(11.26)

Подставляя в виде константы плюс возмущение, получаем уравнение

(11.27)

В скобках дана -статистика свободного члена. Превышение 0,142% за квартал составило четыре стандартных отклонения от нуля. После 1979 г. наступил период более высокой изменчивости, чем в предыдущем периоде наблюдений. Чтобы тестировать наличие АРУГ-ошибок, квадратичные ошибки были представлены регрессией со взвешенным средним квадратичных ошибок

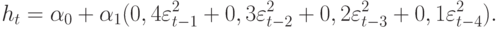
При гипотезе, что 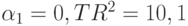, которое должно быть распределено как 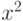с одной переменной степенью свободы. При 1%-ном уровне значимости критическое значение 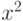-распределения равно 6,635. Следовательно, гетероскедастичность присутствует, без сомнения.

Если существуют АРУГ-ошибки, значит, уравнение (11.27) не отражает суть процесса.

Оценки коэффициентов по методу максимального правдоподобия (ММП-метод) модели АРУГ-М и соответствующие -статистики цитируемой работы приведены ниже:

Оценка 1,64 параметра АРУГ-уравнения показывает, что безусловная дисперсия бесконечная (хотя условная дисперсия конечная). Изменения в величине 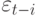ведут к увеличению условной дисперсии. Поэтому и появляются периоды спокойствия и высокой изменчивости. В течение периода высокой изменчивости премия за риск растет.