НОУ ИНТУИТ | Структуры данных и модели вычислений. Лекция 14: Логическое программирование

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 26.09.2006 | Уровень: специалист | Доступ: платный

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать программу

Примеры формальных доказательств

Пример. Вывести из гипотез 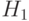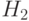H_1 , H_2 , H_3 заключение , где

$\eqa*{ & H_1\colon \forall x [E(x) \& \neg P(x) \to \exists y[R(x, y) \& D(y)]],\\ & H_2\colon \exists x [E(x) \& M(x) \& \forall y[R(x, y) \to M(y)]],\\ & H_3\colon \forall x [M(x) \to \neg P(x)],\\ & C\colon \exists x [M(x) \& D(x)]. }$

Префиксная форма:

$\eqa*{ & {\rm Pref}(H_1)\colon \forall x \,\exists y [E(x) \& \neg P(x) \to [R(x, y) \& D(y)]],\\ & {\rm Pref}(H_2)\colon \exists x \,\forall y [E(x) \& M(x) \& [R(x, y) \to M(y)]],\\ & {\rm Pref}(H_3)\colon \forall x [M(x) \to \neg P(x)],\\ & {\rm Pref}(C)\colon \exists x [M(x) \& D(x)]. }$

Сколемовская форма:

$\eqa*{ & {\rm Sk}(H_1)\colon \forall x [E(x) \& \neg P(x) \to [R(x, f(x)) \& D(f(x))]],\\ & {\rm Sk}(H_2)\colon \forall y [E(a) \& M(a) \& [R(a, y) \to M(y)]],\\ & {\rm Sk}(H_3)\colon \forall x [M(x) \to \neg P(x)],\\ & {\rm Sk}(\neg C)\colon \forall x [\neg M(x) \vee \neg D(x)]. }$

Клаузальная форма (опускаем кванторы общности, а бескванторные части приводим к КНФ и из каждого сомножителя получаем клаузу):

$\eqa*{ & {\rm Cla}(H_1)\colon [\neg E(x) \vee P(x) \vee R(x, f(x)] \& [\neg E(x) \vee P(x) \vee D(f(x))],\\ & {\rm Cla}(H_2)\colon M(a) \& E(a) \& [\neg R(a, y) \vee M(y)],\\ & {\rm Cla}(H_3)\colon \neg P(x) \vee \neg M(x),\\ & {\rm Cla}(C)\colon \neg M(x) \vee \neg D(x). }$

Доказательство с использованием правила резолюции:

$\eqa*{ 1.\ & \neg E(x) \vee P(x) \vee R(x, f(x)) && \t{— из гипотезы}\ H_1,\\ 2.\ & \neg E(x) \vee P(x) \vee D(f(x)) && \t{— из гипотезы}\ H_1,\\ 3.\ & M(a), && \t{— из гипотезы}\ H_2,\\ 4.\ & E(a), && \t{— из гипотезы}\ H_2,\\ 5.\ & \neg R(a, y) \vee M(y), && \t{— из гипотезы}\ H_2,\\ 6.\ & \neg P(x) \vee \neg M(x), && \t{— из гипотезы}\ H_3,\\ 7.\ & \neg M(x) \vee \neg D(x), && \t{— из заключения}\ C,\\ 8.\ & P(a) \vee R(a, f(a)), && \t{— из 1, 4 с помощью подстановки}\ (x/a),\\ 9.\ & P(a) \vee D(f(a)), && \t{— из 2, 4 с помощью подстановки}\ (x/a),\\ 10.\ & \neg P(a), && \t{— из 3, 6 с помощью подстановки}\ (x/a),\\ 11.\ & D(f(a)), && \t{— из 9, 10},\\ 12.\ & \neg M(f (a)) && \t{— из 7, 11 с помощью подстановки}\\ &&& \q (x/f(a)),\\ 13.\ & R(a, f(a)), && \t{— из 8, 10},\\ 14.\ & M(f(a)), && \t{— из 5, 13 с помощью подстановки}\\ &&& \q (y/f(a)),\\ 15.\ & \square && \t{— из 12, 14} }$

Пример. Рассмотрим предикаты с интерпретацией:

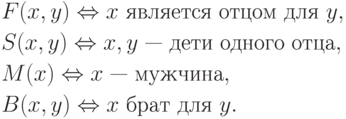
$\eqa*{ & F(x, y) \Leftrightarrow x\ \t{является отцом для}\ y,\\ & S(x, y) \Leftrightarrow x, y\ \t{— дети одного отца},\\ & M(x) \Leftrightarrow x\ \t{— мужчина},\\ & B(x, y) \Leftrightarrow x\ \t{брат для}\ y. }$

В качестве аксиом рассмотрим формулы

$\eqa*{ & A_1\colon \forall x\, \forall y [F(x, y) \to M(x)],\\ & A_2\colon \forall x\, \forall y \, \forall w [F(x, y) \& F(x, w) \to S(y, w)],\\ & A_3\colon \forall x\, \forall y [S(x, y) \& M(x) \to B(x, y)]. }$

Пусть из интерпретации известны факты

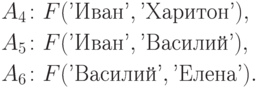
$\eqa*{ & A_4\colon F(\t{'Иван'}, \t{'Харитон'}),\\ & A_5\colon F(\t{'Иван'}, \t{'Василий'}),\\ & A_6\colon F(\t{'Василий'}, \t{'Елена'}). }$

Вопрос: "Есть ли брат у Харитона?" — на языке предикатов записывается как $\eq*{ A_7\colon \exists z\, B(z, \t{'Харитон'})? }$

Доказательство

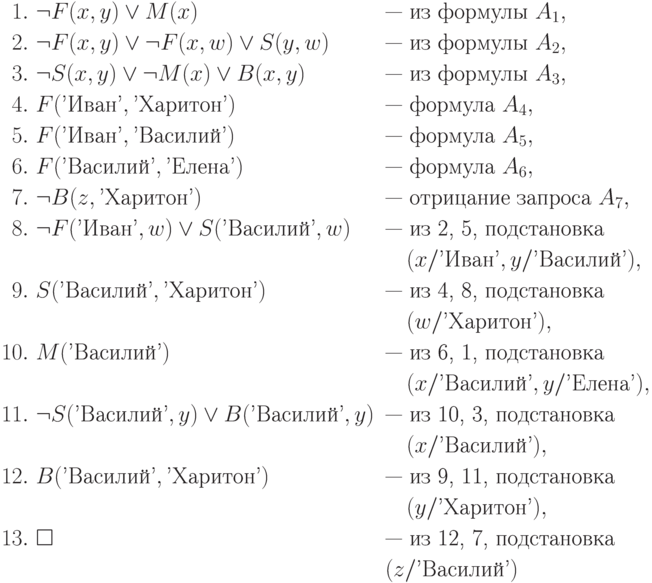
$\eqa*{ 1.\ & \neg F(x, y) \vee M(x) && \t{— из формулы}\ A_1,\\ 2.\ & \neg F(x, y) \vee \neg F(x, w) \vee S(y, w) && \t{— из формулы}\ A_2,\\ 3.\ & \neg S(x, y) \vee \neg M(x) \vee B(x, y) && \t{— из формулы}\ A_3,\\ 4.\ & F(\t{'Иван'}, \t{'Харитон'}) && \t{— формула}\ A_4,\\ 5.\ & F(\t{'Иван'}, \t{'Василий'}) && \t{— формула}\ A_5,\\ 6.\ & F(\t{'Василий'}, \t{'Елена'}) && \t{— формула}\ A_6,\\ 7.\ & \neg B(z, \t{'Харитон'}) && \t{— отрицание запроса}\ A_7,\\ 8.\ & \neg F(\t{'Иван'}, w) \vee S(\t{'Василий'}, w)&& \t{— из 2, 5, подстановка}\\ &&& \q (x/\t{'Иван'}, y/\t{'Василий'}),\\ 9.\ & S(\t{'Василий'}, \t{'Харитон'}) && \t{— из 4, 8, подстановка}\\ &&& \q (w/\t{'Харитон'}),\\ 10.\ & M(\t{'Василий'}) && \t{— из 6, 1, подстановка}\\ &&& \q (x/\t{'Василий'}, y/\t{'Елена'}),\\ 11.\ & \neg S(\t{'Василий'}, y) \vee B(\t{'Василий'}, y) && \t{— из 10, 3, подстановка}\\ &&& \q (x/\t{'Василий'}),\\ 12.\ & B(\t{'Василий'}, \t{'Харитон'}) && \t{— из 9, 11, подстановка}\\ & & & \q (y/\t{'Харитон'}),\\ 13.\ & \square && \t{— из 12, 7, подстановка}\\ & & & (z/\t{'Василий'}) }$

Фактически мы не только получили ответ на наш запрос, но и подтвердили его конкретным значением переменной . Приведенный вывод можно модифицировать, если ввести предикат ${\rm answer}(z)$ и вместо цели

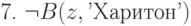
$\eq*{ \t{"}7.\ \neg B(z, \t{'Харитон'})\t{"}\vspace{-1mm} }$

поставить новую цель

$\eqa*{ 7'.\ & \neg B(z, \t{'Харитон'}) \vee {\rm answer}(z).\ \t{Тогда шаг 13 превратится в 13'}.\\ 13'.\ & {\rm answer}(\t{'Василий'})\t{ — из 12, 7', подстановка}\ (z/\t{'Василий'}). }$

Упражнение

Рассмотрите вывод, в котором первые 7 формул являются посылками. Для остальных формул выпишите пояснения к применению правила резолюции.

$\eqa*{ 1.\ & \neg A(z),\\ 2.\ & A(x) \vee \neg P(x) \vee \neg Q(x, y),\\ 3.\ & A(x) \vee \neg R(y) \vee \neg Q(y, x),\\ 4.\ & P(a),\\ 5.\ & Q(b, c),\\ 6.\ & R(a),\\ 7.\ & R(b),\\ 8.\ & \neg P(z) \vee \neg Q(z, y),\\ 9.\ & \neg Q(a, y),\\ 10.\ & \neg R(y) \vee \neg Q(y, z),\\ 11.\ & \neg Q(a, z),\\ 12.\ & \neg Q(b, z),\\ 13.\ & \square }$

Дальше >>

Структуры данных и модели вычислений

Структуры данных и модели вычислений

Логическое программирование

Вопросы и ответы

Студенты

Авторизоваться

Структуры данных и модели вычислений

Структуры данных и модели вычислений

Логическое программирование

Вопросы и ответы

Студенты