НОУ ИНТУИТ | Структуры данных и модели вычислений. Лекция 14: Логическое программирование

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 26.09.2006 | Уровень: специалист | Доступ: платный

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать программу

Некоторые сведения из математической логики

Напомним кратко основную цепочку построений математической логики, используемых в логическом программировании. Известно, что любое предложение в логике предикатов логически равносильно предложению в предваренной нормальной форме, то есть в такой форме, когда в начале расположены все ее кванторы, за которыми расположена бескванторная ее часть. Рассмотрим пример такой формулы

$\eq{ \forall x\, \exists z\, \forall y\, \exists u\, \forall v [P(x, y) \& R(y, z) \to S(x, u, v) \& [S(y, u, v) \vee S(z, y, v)]], }$

( 1)

где

— предикатные символы соответствующей арности; x, y, z, u

,

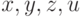— индивидные переменные.

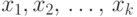Известно, что по любому предложению в предваренной нормальной форме можно построить так называемое сколемовское предложение . Для этого избавляются от кванторов существования следующим образом. Пусть ( — самое левое вхождение квантора существования в рассматриваемую формулу и перед ним расположены кванторов общности с переменными $x_1, x_2\dts x_k$ . 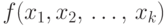Выбираем новый -местный функциональный символ , вхождение $\exists z$ удаляем из формулы, а каждое вхождение переменной заменяем термом $f(x_1, x_2\dts x_k)$ . Аналогичным образом избавляемся и от других кванторов существования. В результате получим сколемовскую формулу для исходной формулы .

Так, для формулы (1) соответствующая сколемовская формула будет иметь вид

$\forall x\, \forall y\, \forall v [[P(x, y) \& R(y, f(x)) \to \\ \to S(x, g(x, y), v)] \& [S(y, g(x, y), v) \vee S(g(x, y), y, v)]],$

( 2)

полученный из (1) заменой

на

, а

на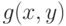

. Заметим, что если бы было k = 0

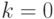, то переменная

заменялась бы на новую константу. Процесс получения сколемовской формулы по заданной формуле

называется сколемизацией.

Известно, что сколемовская формула , соответствующая формуле , может быть логически неравносильна формуле , однако они либо обе выполнимы, либо обе невыполнимы (равносильность по выполнимости). Для иллюстрации этого факта рассмотрим простую формулу

$\eq*{ \forall x\, \exists y R(x, y), }$

которая интуитивно выражает существование функции

, такой, что для любого элемента

выполняется

. При сколемизации она превращается в формулу

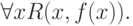
$\eq*{ \forall x R(x, f(x)). }$

Равносильность по выполнимости формулы и соответствующей ей сколемовской формулы может быть использована следующим образом. Предположим, мы хотим доказать, что формула является логическим следствием формул и . Это сводится к доказательству невыполнимости формулы

$\eq*{ [A \& B \& \neg C] }$

или соответствующей ей сколемовской формулы, что технически осуществить оказывается проще.

Поскольку в сколемовской формуле используются только кванторы общности и все они расположены в начале формулы, их обычно опускают, подразумевая по умолчанию их наличие, а бескванторную часть представляют в нормальной конъюнктивной форме. Полученная таким образом формула называется клаузальной. В нашем случае формула (2) превращается в клаузальную формулу

$\eq{ [\neg P(x, y) \vee \neg R(y, f(x)) \vee S(x, g(x, y), v)] \&\\ \& [S(y, g(x, y), v) \vee S(g(x, y), y, v)]. }$

( 3)

Упомянутый выше метод резолюций основывается на единственном правиле вывода, называемом правилом резолюции, которое заключается в следующем. Из двух формул вида

$\eq*{ [\neg A \vee B_1 \vee B_2 \vee \ldots \vee B_k] }$

и

$\eq*{ [A \vee D_1 \vee D_2 \vee \ldots \vee D_s] }$

в соответствии с правилом резолюции выводится формула

$\eq*{ [B_1 \vee B_2 \vee \ldots \vee B_k \vee D_1 \vee D_2 \vee \ldots \vee D_s]. }$

Видно, что клаузальная форма хорошо приспособлена для применения правила резолюции. Детали этого применения в логике предикатов будут рассмотрены ниже.

Из математической логики известно, что не существует алгоритма, который по любому множеству формул-гипотез логики предикатов и еще одной формуле отвечал бы на вопрос, является ли логическим следствием множества . Однако существует алгоритм, который в случае, когда логически следует из , строит доказательство этого факта с использованием правила резолюции, в противном случае алгоритм может работать бесконечно.

Различные версии языка Пролог базируются на использовании так называемых хорновских клаузальных формул. Хорновскими называются формулы, являющиеся дизъюнкциями атомарных формул и/или их отрицаний, причем атомарная часть без отрицания может быть в такой формуле не более чем одна. Рассмотрим пример такой формулы:

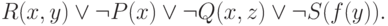$\eq{ R(x, y) \vee \neg P(x) \vee \neg Q(x, z) \vee \neg S(f(y)). }$

( 4)

Ее можно представить в виде

$\eq{ P(x) \& Q(x, z) \& S(f(y)) \to R(x, y). }$

( 5)

Эта формула воспринимается Прологом так, как если бы все ее переменные были связаны квантором общности. Восстанавливая кванторы, имеем

$\eq{ \forall x \, \forall y \, \forall z [P(x) \& Q(x, z) \& S(f(y)) \to R(x, y)]. }$

( 6)

Учитывая, что

не входит в правую часть импликации, формулу (6) можно переписать в виде

$\eq*{ \forall x\, \forall y [\exists z [P(x) \& Q(x, z) \& S(f(y))] \to R(x, y)], }$

изменив область действия квантора $\exists z$ .

В Прологе принято формулы, аналогичные формуле (5), записывать в виде

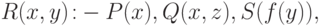$\eq{ R(x, y)\colon\!\!-P(x), Q(x, z), S(f(y)), }$

( 7)

меняя местами левую и правую части импликации и вместо знака конъюнкции ставя запятую.

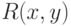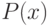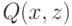Формулу (7) Пролог воспримет как указание на то, что для доказательства истинности R(x, y) надо найти некоторое значение и доказать, что истинны P(x) , Q(x, z) , S(f(y)) . Такие формулы принято называть правилами.

Если в хорновской клаузальной формуле отсутствуют атомарные части с отрицанием, то такая формула называется фактом. Если в хорновской клаузальной формуле отсутствует атомарная часть без отрицания, то такая формула называется запросом. Программой в Прологе называется набор фактов и правил.

По заданной программе и запросу система Пролог определяет, является ли запрос логическим следствием фактов и правил программы. При этом если в запросе имеются свободные переменные, то в процессе поиска доказательства эти переменные конкретизируются, то есть принимают конкретные значения, и при успешном его завершении эти конкретизированные значения являются ответом к поставленной задаче. Если же доказательство не будет найдено, то система ответит "no".

Дальше >>

Структуры данных и модели вычислений

Структуры данных и модели вычислений

Логическое программирование

Некоторые сведения из математической логики

Вопросы и ответы

Студенты

Авторизоваться

Структуры данных и модели вычислений

Структуры данных и модели вычислений

Логическое программирование

Некоторые сведения из математической логики

Вопросы и ответы

Студенты