Абак, алгорифмы Маркова, равнодоступная адресная машина

Примеры неразрешимости

Функцию 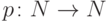назовем вычислимой на абаке, если существует программа , которая, получив в некоторой, заранее обусловленной ячейке значение аргумента , а в остальных ячейках — нули, через конечное число шагов остановится, и в ячейке будет находиться .

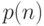Проблема построения невычислимой функции известна как "проблема усердного бобра". Пусть — абак-программа и — номер некоторой ячейки. Определим величину 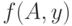следующим образом. Если в начальный момент все ячейки содержат число 0 и программа через конечное число шагов останавливается, то 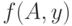равно числу в момент остановки. Если же программа работает бесконечно, то считаем . Величину 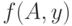назовем -продуктивностью программы .

Обозначим через множество всех абак-программ, состоящих из команд. Определим функцию 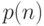как максимум 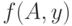по всем программам из и ячейкам . Очевидно, эта функция определена при всех натуральных значениях аргумента и строго монотонна.

Лемма. Для любого натурального числа выполняется неравенство

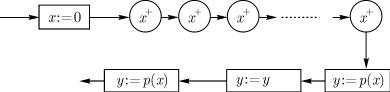
Для доказательства достаточно рассмотреть программу, которая сначала запишет в ячейку , затем прибавит к ней раз 1, скопирует содержимое ячейки в ячейку и добавит к ней содержимое ячейки . Очевидно, после выполнения такой программы в ячейке будет число , а подсчет числа команд показывает, что их будет . Наличие такой программы (рис. 12.1) доказывает требуемое неравенство.

Рис. 12.1.

Предположим теперь, что 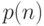вычислима некоторой программой , состоящей из команд, которая, получив в ячейке , поместит ответ в ячейку .

Тогда для каждого натурального можно построить программу, вычисляющую , состоящую из команд. Эта программа сначала запишет в ячейку , затем прибавит к ней раз единицу, затем с помощью программы в ячейке вычислит 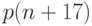, скопирует в и, наконец, опять с помощью программы вычислит .

Наличие такой программы (рис. 12.2) означало бы, что при любом натуральном выполняется неравенство

Поскольку функция 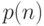монотонна, получаем

Сопоставляя это неравенство с неравенством в утверждении леммы, получим

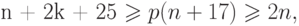
что приводит к противоречию, например, при .

Итак, предположение о вычислимости функции 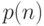привело к противоречию.

Рис. 12.2.

На рис. 12.2 команда 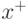повторяется раз, общее количество команд в программе 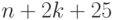, в ячейке вычисляется .

Рассмотрим произвольную инъективную нумерацию программ, то есть нумерацию, ставящую в соответствие каждой программе ее номер , причем разным программам ставятся в соответствие разные номера. Программу назовем самоприменимой относительно ячейки , если она, получив в ячейке свой номер, а в остальных ячейках — нули, через конечное число шагов завершает вычисления.

Рассмотрим функцию 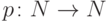, определяемую следующим образом:

• , если является номером некоторой самоприменимой относительно ячейки программы,
• , в противном случае.

Докажем, что функция не вычислима никакой программой. Предположим, что вычисляется программой , которая, получив в ячейке число , остановится через конечное число шагов и в ячейке оставит 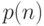. Рассмотрим программу 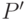, изображенную на рис. 12.3.

Рис. 12.3.

Если 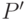самоприменима относительно ячейки , то , поэтому, когда проработает программа , в ячейке будет записана 1 и остальная часть программы — будет работать без остановки. Следовательно, — не самоприменима относительно .

Если же 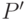не самоприменима относительно ячейки , то 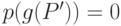, следовательно, когда проработает программа , в ячейке будет записан 0 и тогда остальная часть программы — сразу же завершит работу. Следовательно, — самоприменима относительно .

Итак, предположение о вычислимости функции 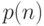в любом случае приводит к противоречию.