| Россия, г. Москва |
Рынок как система с явными потерями
3.3. Стационарный режим. Распределение Эрланга
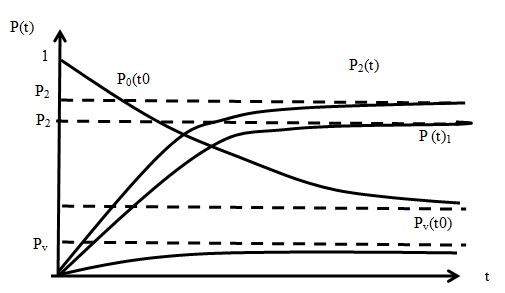
Естественно принять начальные условия:
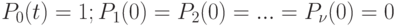
При начале работы рынка 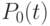 будет уменьшаться,
будет уменьшаться,
а далее 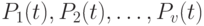 - возрастать. Но беспредельно вероятности возрастать не могут.
- возрастать. Но беспредельно вероятности возрастать не могут.
Доказано, что для систем с явными потерями переходный процесс затухает, и система при  переходит в стационарный режим, так называемый установившийся режим обслуживания, то есть при
переходит в стационарный режим, так называемый установившийся режим обслуживания, то есть при  все вероятности
все вероятности 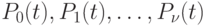 стремятся к постоянным пределам
стремятся к постоянным пределам 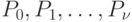 ; а все их производные - к нулю.
; а все их производные - к нулю.
Чтобы найти предельные вероятности 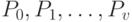 (вероятности состояний системы в установившемся режиме), заменим в уравнениях Эрланга все вероятности
(вероятности состояний системы в установившемся режиме), заменим в уравнениях Эрланга все вероятности  , их пределами
, их пределами 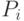 , а все производные положим равным нулю. Получим следующую систему алгебраических уравнений:
, а все производные положим равным нулю. Получим следующую систему алгебраических уравнений:
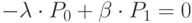 ,
,
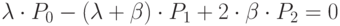 ,
,
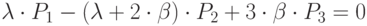
…
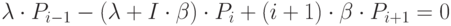 ,
, 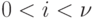
…
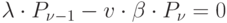 |
( 3.8) |
К этим уравнениям необходимо добавить условие  .
.
Решим систему этих уравнений относительно 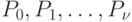 .
.
Из первого уравнения имеем
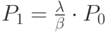
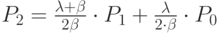
Из второго - 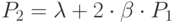 .
.
Подставляя вместо 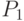 значение, выраженное из первого уравнения, получим:
значение, выраженное из первого уравнения, получим:
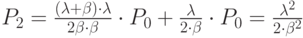
Обобщённый вид формулы:
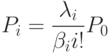 |
( 3.9) |
Посмотрим, что собой представляет отношение 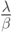 :
:
 - это параметр потока, численно равный для простейшего потока интенсивности, то есть среднему числу партий товаров в единицу времени;
- это параметр потока, численно равный для простейшего потока интенсивности, то есть среднему числу партий товаров в единицу времени;
- математическое ожидание средней длительности потребления одной партии товаров.
Следовательно, 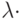 - есть интенсивность поступающего предложения
- есть интенсивность поступающего предложения

Выражение для P_i перепишется в следующем виде:

Для определения 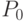 воспользуемся условием нормировки
воспользуемся условием нормировки
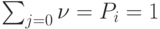 ,
,

отсюда

Окончательно выражение для 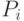 примет вид:
примет вид:
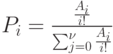
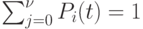
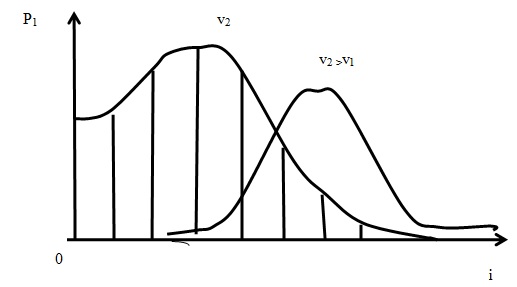
Огибающие:
При 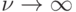 распределение Эрланга переходит в распределение Пуассона.
распределение Эрланга переходит в распределение Пуассона.
Эту формулу часто обозначают следующим образом:
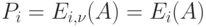 - вероятность того, что в произвольный момент
- вероятность того, что в произвольный момент
времени стационарного режима в полнодоступной группе ёмкостью 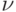 потребителей, на которую поступает интенсивность партий товаров
потребителей, на которую поступает интенсивность партий товаров  , создаваемая простейшим потоком товаров, занято
, создаваемая простейшим потоком товаров, занято  потребителей.
потребителей.
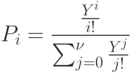 |
( 3.11) |