| Казахстан |
Разработка полноценных Windows-приложений
3. Построение системы линейных уравнений и ее решение
Для построения системы линейных уравнений будем использовать шаблонный класс матриц matrix<type>. Этот класс выделен в отдельный заголовочный файл matrix.h. Его необходимо скопировать в каталог с проектом и добавить в проект с помощью утилиты Solution Explorer (вызвать контекстное меню проекта в окне утилиты Solution Explorer  Add
Add  Existing item… и далее указать имя файла). Полный код класса приведен в приложении. Напишем функции для поиска обратной матрицы. Введем их в файле RegrDlg.cpp после строк.
Existing item… и далее указать имя файла). Полный код класса приведен в приложении. Напишем функции для поиска обратной матрицы. Введем их в файле RegrDlg.cpp после строк.
#include "stdafx.h" #include "Regr.h" #include "RegrDlg.h" #ifdef _DEBUG #define new DEBUG_NEW #endif
Функции для поиска обратной матрицы:
//Функции для решения СЛАУ методом окаймления
matrix<double> bordering (matrix<double> u, matrix<double> v,
matrix<double> A, matrix<double> a)
{
matrix<double> b = a - u*A*v;
b.setcell(1/b.getcell(0,0),0,0);
matrix<double> s = -u*A*b.getcell(0,0);
matrix<double> w = -A*v*b.getcell(0,0);
matrix<double> B = A - A*v*s;
B.addcolend(w);
s.addcolend(b);
B.addrowend(s);
return B;
}
matrix>double> getreverse (matrix<double> M)
{
matrix<double> Res;
if(M.getcolsize() == M.getrowsize())
{
Res = M.getminor(0,0,0,0);
Res.setcell(1/Res.getcell(0,0),0,0);
for(uni i = 1; i < M.getcolsize(); i++)
{
matrix<double> v = M.getminor(i,0,i,i-1);
matrix<double> u = M.getminor(0,i,i-1,i);
matrix<double> a = M.getminor(i,i,i,i);
Res = bordering(u,v,Res,a);
}
}
return Res;
}Для формирования и решения системы мы создали кнопку Start approximation. Обработаем нажатие на нее. Обработчик нажатия на кнопку Start approximation:
void CRegrDlg::OnBnClickedButtonStart()
{
UpdateData(true);
CRichEditCtrl *pRich = (CRichEditCtrl *) GetDlgItem(IDC_RICHEDIT_RES); //Переменная для управления RichEditom
if(mNum >= mInitArr.GetSize()) //Если данные не соответствуют
{
pRich->SetWindowTextA(CString("Number of points mismatches approximation degree")); //Выводим предупреждение
return; //Выходим
}
mNodeMatrix.setsize(mNum + 1,mNum + 1); //Задаем размерность матрицы для поиска коэффициентов
int n = (int) mInitArr.GetSize();
for(int i = 0; i < mNum + 1; i++) //Идем по строкам матрицы
for(int j = 0; j < mNum + 1; j++) //Идем по столбцам матрицы
{
double elem = 0; //вспомогательная переменная
for(int k = 0; k < n; k++) //Идем по точкам таблицы
elem += pow(mInitArr[k].x,(double)i+j); //Формируем элемент матрицы
mNodeMatrix.setcell(elem/n,j,i); //Инициализируем элемент матрицы
}
mRightPart.setsize(1,mNum + 1); //Задаем размерностьправой части системы
for(int i = 0; i < mNum + 1; i++) //Идем по строкам правой части
{
double elem = 0; //Вспомогательный элемент
for(int k = 0; k < n; k++) //Идем по точкам таблицы
elem += mInitArr[k].y*pow(mInitArr[k].x,(double)i); //Формируем элемент правой части
mRightPart.setcell(elem/n,0,i); //Инициализируем элемент правой части
}
matrix<double> Solution(::getreverse(mNodeMatrix)*mRightPart); //Решаем уравнение
CString str; //Строка для вывода результатов
str.Format("f(x) = %f",Solution.getcell(0,0));
//Формируем строку полинома
for(uni i = 1; i < Solution.getrowsize(); i++)
{
CString temp;
temp.Format(" + %f*x^%d",Solution.getcell(0,i),i);
str += temp;
}
pRich->SetWindowTextA(str); //Выводим ее
}4. Вывод информации
Вывод осуществляется в двух направлениях: вывод таблицы узлов и вывод аналитической формулы полинома. За вывод узлов отвечает элемент управления списковое представление, код вывода точек в таблице представлен в обработчиках кнопок Add и Delete. За вывод формулы полинома отвечает элемент управления текстовое поле с форматированием, код вывода формулы приведен в обработчике кнопик Start approximation. Для завершения программы добавим строку:
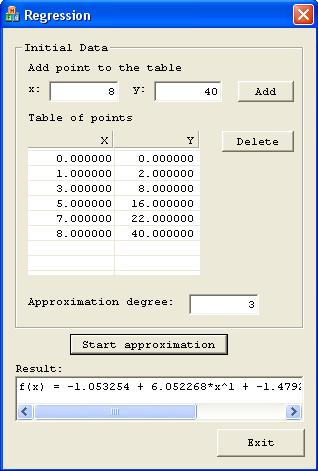
#include "matrix.h"
в файл RegrDlg.h перед описанием класса SDPoint. Скомпилируем и запустим приложение. В результате в соответствии с введенными данными должно получиться следующее: рис. 5.10