| Украина |
Список задач
Отметим, что во время обучения студентам также предлагались для решения более простые учебные задачи, которые мы здесь не приводим. Эти задачи, а также лучшие компьютерные визуализации, полученные студентами во время прохождения Практикума, выложены на сайте http://dfgm.math.msu.su кафедры дифференциальной геометрии и приложений механико-математического факультета МГУ. Там же можно найти и другие материалы по компьютерной геометрии.
Задачи первого семестра
Задача 1.1. Для заданной гладкой кривой  и произвольной ее точки
и произвольной ее точки 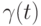 найти кривую второго порядка
найти кривую второго порядка  , проходящую через
, проходящую через 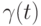 и приближающую
и приближающую  с четвертым порядком (при некоторой параметризации кривой
с четвертым порядком (при некоторой параметризации кривой  производные этих кривых вплоть до четвертого порядка совпадают). Отметим, что такая кривая
производные этих кривых вплоть до четвертого порядка совпадают). Отметим, что такая кривая  однозначно определена. Визуализировать изменение кривой
однозначно определена. Визуализировать изменение кривой  при изменении точки
при изменении точки 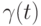 .
.
Задача 1.2. Эволютой или каустикой регулярной кривой называется множество ее центров кривизны. Далее, кривая  , перпендикулярная ко всем касательным некоторой гладкой кривой
, перпендикулярная ко всем касательным некоторой гладкой кривой  , называется эвольвентой этой кривой. Отметим, что эволюта определена однозначно, в то время как эвольвент, вообще говоря, много (эвольвента зависит от своей начальной точки). Для заданной гладкой кривой построить семейство ее эвольвент, динамически зависящее от параметра. Проиллюстрировать теорему о том, что исходная кривая является одной из эвольвент своей эволюты.
, называется эвольвентой этой кривой. Отметим, что эволюта определена однозначно, в то время как эвольвент, вообще говоря, много (эвольвента зависит от своей начальной точки). Для заданной гладкой кривой построить семейство ее эвольвент, динамически зависящее от параметра. Проиллюстрировать теорему о том, что исходная кривая является одной из эвольвент своей эволюты.
Задача 1.3. Используя интерполяционный многочлен, построить график гладкой функции, проходящей через заданные локаторами ( Locator ) точки. Для двух таких функций 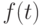 и
и 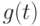 построить кривую с кривизной
построить кривую с кривизной 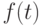 и кручением
и кручением 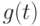 , где
, где  - натуральный параметр. Реализацию кривой выполнить таким образом, чтобы изменение функций
- натуральный параметр. Реализацию кривой выполнить таким образом, чтобы изменение функций  и
и  посредством смещения локаторов мгновенно приводило бы к пересчету соответствующей кривой и визуализации ее обновления.
посредством смещения локаторов мгновенно приводило бы к пересчету соответствующей кривой и визуализации ее обновления.
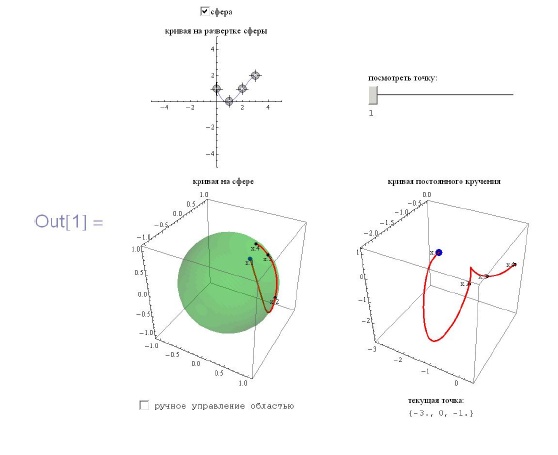
Задача 1.4. Доказать, что кривые постоянной кривизны 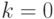 задаются так:
задаются так:
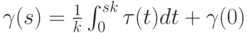
где 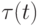 - натурально параметризованная кривая на единичной сфере. Визуализируйте задание кривых на сфере в сферических координатах с помощью локаторов. По каждой такой кривой вычислите соответствующую пространственную кривую постоянной кривизны. Реализацию сделайте такой, чтобы изменения сферической кривой приводили к мгновенным изменениям соответствующей пространственной кривой.
- натурально параметризованная кривая на единичной сфере. Визуализируйте задание кривых на сфере в сферических координатах с помощью локаторов. По каждой такой кривой вычислите соответствующую пространственную кривую постоянной кривизны. Реализацию сделайте такой, чтобы изменения сферической кривой приводили к мгновенным изменениям соответствующей пространственной кривой.
Задача 1.5. То же для кривых постоянного кручения.
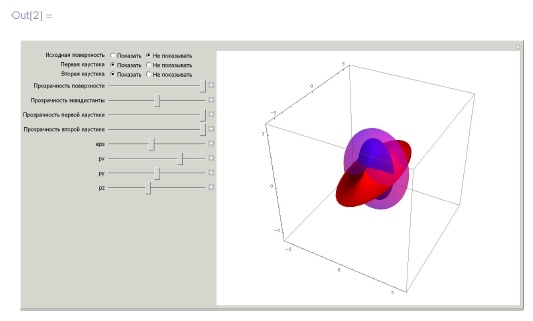
Определение 9.1.1. Эквидистантой или, более точно,  - эквидистантой параметрически заданной регулярной поверхности
- эквидистантой параметрически заданной регулярной поверхности 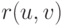 с полем нормалей
с полем нормалей 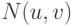 называется поверхность
называется поверхность 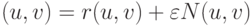 . Ясно, что при малых
. Ясно, что при малых  эквидистанта регулярна. С ростом
эквидистанта регулярна. С ростом  могут возникать точки, в которых регулярность нарушается - так называемые особые точки.
могут возникать точки, в которых регулярность нарушается - так называемые особые точки.
Задача 1.6. Для поверхности, заданной параметрически, динамически визуализировать волновой фронт (эквидистанту, меняющуюся при смещении ползунка). Визуализируйте среднюю и гауссовы кривизны эквидистант, раскрасив поверхность в соответствии с этими функциями. Исследуйте поведение этих функций в окрестностях особенностей эквидистант.
Задача 1.7. Для поверхности, заданной параметрически, динамически визуализировать волновой фронт (эквидистанту, меняющуюся при смещении ползунка). Раскрасьте поверхность в три цвета в зависимости от типа точек (эллиптический, гиперболический, параболический). (Точка регулярной поверхности называется эллиптической, если главные кривизны одного знака, гиперболической, если они разного знака, но не нулевые, параболической - в остальных случаях.) Исследуйте поведение этих типов в окрестностях особенностей эквидистант.
Задача 1.8. Для поверхности, заданной параметрически, динамически визуализировать волновой фронт (эквидистанту, меняющуюся при смещении ползунка), а также семейство линий кривизны на этих эквидистантах. (Кривая на поверхности называется линией кривизны, если ее вектор скорости в каждой точке направлен вдоль главного направления.) Что происходит с линиями кривизны при возникновении особенностей на эквидистантах?
Задача 1.9. Для поверхности, заданной графиком функции, визуализировать плоское нормальное сечение при динамически меняющихся направлении и точке (визуализировать также точку на поверхности). Построить график кривизны со знаком как функции направления сечения (меняющийся в зависимости от точки). При каждом конкретном сечении отметить на построенном графике соответствующую точку, а также точки, соответствующие главным направлениям. Проиллюстрируйте справедливость формулы Эйлера.
Задача 1.10. Для поверхности, заданной графиком функции, визуализировать плоское сечение, проходящее через фиксированную точку поверхности, при динамически меняющихся направлении сечения и нормали  в плоскости сечения к направлению этого сечения (визуализировать точку и нормаль
в плоскости сечения к направлению этого сечения (визуализировать точку и нормаль  ). Построить меняющийся в зависимости от направления график кривизны со знаком как функции нормали
). Построить меняющийся в зависимости от направления график кривизны со знаком как функции нормали  . При каждом конкретном сечении отметить на построенном графике соответствующую точку, а также точку, соответствующую нормальному сечению. Проиллюстрируйте справедливость теоремы Менье.
. При каждом конкретном сечении отметить на построенном графике соответствующую точку, а также точку, соответствующую нормальному сечению. Проиллюстрируйте справедливость теоремы Менье.
Задача 1.11. Для данной поверхности изобразить каустику (множество центров кривизны). Реализовать там же распространение волнового фронта (семейство эквидистант). На примере эллипсоида убедиться, что особенности всех волновых фронтов образуют каустику.
Задача 1.12. Для замкнутой кривой (заданной линией уровня функции) написать динамическую модель биллиарда. Реализовать динамическую зависимость поведения биллиарда от формы кривой, меняющейся при изменении параметров функции. Предусмотреть возможность запоминания траектории и ее визуализацию.
Определение 9.1.2. Геодезической на поверхности называется регулярная кривая, ускорение которой перпендикулярно поверхности.
Задача 1.13. Для данной поверхности визуализировать геодезическую, выходящую из данной точки в данном направлении. Обеспечить динамическое изменение точки, направления и длины геодезической. Изучить поведение геодезических на поверхности вращения (визуализировать теорему Клеро об угле между геодезической и меридианом).
Задача 1.14. Для данной поверхности визуализировать геодезическую, соединяющую две данные точки. Обеспечить динамическое изменение точек. Построить поверхность, на которой некоторые две точки соединяются более чем одной геодезической. Визуализировать эти точки и геодезические.
Задача 1.15. Реализовать динамическую модель многогранника заданной структуры, координаты вершин которого можно менять интерактивно. Реализовать движение точечной массы вдоль поверхности многогранника по геодезической (на грани - вдоль отрезка прямой; переход с грани на грань - прямолинейный на соответствующей развертке). Траектория должна чувствовать изменение координат вершин многогранника. Предусмотреть возможность запоминания траектории и ее визуализацию.
Задача 1.16. Визуализировать плоские сечения многогранников, заданные тремя точками, каждая из которых лежит на некотором ребре. Предусмотреть динамическую зависимость сечения от положения точек на ребрах и от координат вершин многогранников. Определить максимальное число сторон сечения данного направления для фиксированного многогранника.
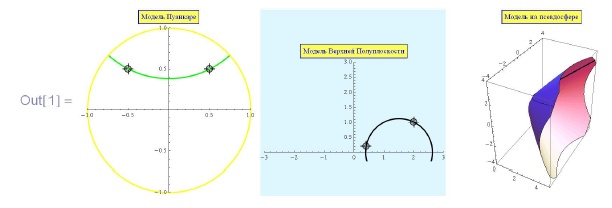
Задача 1.17. Визуализировать связь между точками и прямыми геометрии Лобачевского в модели на псевдосфере, модели Пуанкаре (стереографическая проекция на круг) и модели верхней полуплоскости. Обеспечить динамическую связь точек и прямых.
Задача 1.18. Визуализировать связь между точками и прямыми геометрии Лобачевского в модели на псевдосфере, модели Пуанкаре и модели Клейна (центральная проекция на плоскость, касающуюся псевдосферы в ее полюсе). Обеспечить динамическую связь точек и прямых.
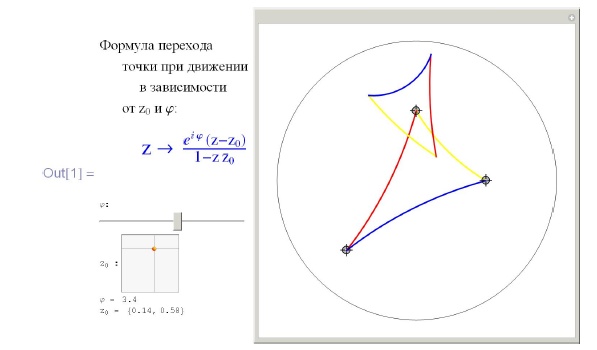
Задача 1.19. Задать трехпараметрическую группу собственных движений плоскости Лобачевского с помощью Manipulate. Реализовать возможность задания и деформации многоугольника на плоскости Лобачевского с помощью мышки. Предусмотреть возможность изменения заданного многоугольника под действием группы изометрий (при смещении ползунков).
Определение 9.1.3. Движение плоскости Лобачевского называется гиперболическим, эллиптическим или параболическим, если оно имеет 2, 0 и 1 неподвижную точку на абсолюте соответственно. Гиперболическое движение называется сдвигом. Оно переводит в себя ровно одну прямую на плоскости Лобачевского, а именно, прямую, соединяющую неподвижные точки на абсолюте. Каждая точка этой прямой ( оси сдвига ) смещается вдоль этой прямой на одно и то же расстояние, называемое величиной сдвига. Эллиптическое движение однозначно задается неподвижной точкой в конечной области плоскости Лобачевского и вещественным параметром - углом поворота. Наконец, параболическое движение переводит друг в друга прямые, проходящие через его неподвижную точку на абсолюте. Оно задается этой точкой и вещественным параметром.
Задача 1.20. Задать гиперболический сдвиг (заданный своей осью и величиной смещения), эллиптическое преобразование (определенное неподвижной точкой и углом поворота), параболический сдвиг (заданный неподвижной точкой на абсолюте и величиной сдвига). Визуализировать эти преобразования на примере их действия на некоторый треугольник. Изобразить соответствующие инвариантные пучки геодезических и орициклов.
Задача 1.21. На плоскости Лобачевского визуализировать треугольник с углами величины 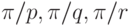 , где
, где 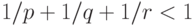 . Проиллюстрировать теорему о том, что плоскость Лобачевского допускает замощение изометричными образами этого треугольника. Предусмотреть возможность изменения параметров
. Проиллюстрировать теорему о том, что плоскость Лобачевского допускает замощение изометричными образами этого треугольника. Предусмотреть возможность изменения параметров 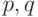 и
и 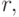 а также "начального" положения треугольника. Подобрать
а также "начального" положения треугольника. Подобрать 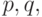 и
и  так, чтобы построенное замощение порождало замощение плоскости Лобачевского 4g -угольниками с суммарным углом
так, чтобы построенное замощение порождало замощение плоскости Лобачевского 4g -угольниками с суммарным углом 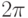 такими, что их стороны с номерами i и i + 2g имеют одинаковые длины. Визуализировать полученное замощение.
такими, что их стороны с номерами i и i + 2g имеют одинаковые длины. Визуализировать полученное замощение.
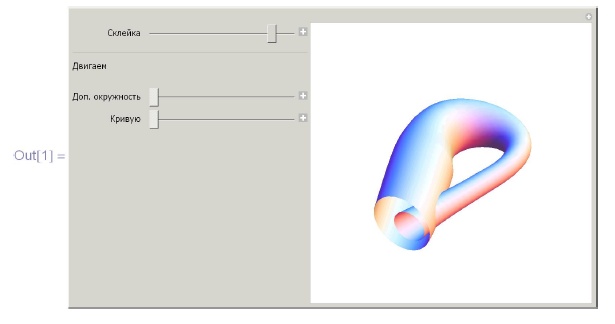
Задача 1.22. Визуализировать склейку тора из квадрата. Проиллюстрировать его ориентируемость, протащив репер вдоль петель, соответствующих сторонам квадрата.
Задача 1.23. Визуализировать склейку бутылки Клейна из квадрата. Проверить ее неориентируемость, протащив вдоль некоторой петли репер так, чтобы он изменил ориентацию.
Задача 1.24. Визуализировать склейку проективной плоскости из квадрата. Проверить ее неориентируемость, протащив вдоль некоторой петли репер так, чтобы он изменил ориентацию.
Задача 1.25. Визуализировать скрученную полосу (0-скрученная полоса - цилиндр; однократно скрученная полоса - лист Мебиуса; двукратно скрученная полоса гомеоморфна цилиндру). Визуализировать кратное разрезание скрученной полосы (т. е. ее и полученных при разрезании скрученных полос) вдоль средних линий. Визуализировать тест на ориентируемость непрерывным перемещением (с помощью ползунка) репера вдоль средней линии полученной скрученной полосы.
Задача 1.26. Разрезать бутылку Клейна и убедиться, что она составлена из двух листов Мебиуса. Вырезать из проективной плоскости диск и убедиться, что оставшаяся часть - лист Мебиуса.
Задача 1.27. Реализовать на поверхности вращения графика функции локсодрому (кривую, пересекающую меридианы под заданным углом). Предусмотреть динамическое изменение угла, длины кривой, начальной точки.
Задача 1.28. Визуализировать деформацию сферы с ручкой и листом Мебиуса в сферу с тремя листами Мебиуса. Продемонстрировать неориентируемость.
Задача 1.29. Визуализировать приклейку листов Мебиуса к сфере с дырками. Получить так проективную плоскость (когда дырка одна) и бутылку Клейна (когда дырки две).