| Украина |
Список задач
Задачи второго семестра
Задача 2.1. Написать программу деления поверхности Безье на четыре части. Исходные опорные точки и точку деления выбирать динамически. Вывести новые опорные точки динамически и проверить, что после деления полученные части меняются независимо друг от друга при изменении их опорных точек.
Задача 2.2. Написать программу добавления новых узлов в сетку Безье без изменения самой поверхности. Количество точек задавать динамически.
Задача 2.3. Дан прямоугольник на плоскости (предположим, что он эластичен, т. е. может растягиваться и менять свою площадь). С помощью выдавливания сделать из него форму для льда. Использовать B -поверхность.
Задача 2.4. Дан прямоугольник на плоскости (предположим, что он эластичен, т. е. может растягиваться и менять свою площадь). Выдавить из него букву O. Использовать поверхность перехода.
Задача 2.5. Изобразить решение задачи 7.66 из задачника [5], т. е. посредством гладкой изотопии расцепить две зацепленные ручки.
Задача 2.6. Дан куб. Скруглить его вершины динамически. Класс гладкости должен равняться C1. Проверить условие гладкости формулами.
Задача 2.7. Дан диск. Берем ручку, т. е. цилиндр, и приклеиваем один конец ручки к одной стороне диска, а другой - ко второй стороне диска. Изобразить деформацию диска, дающую бутылку Клейна, из которой вырезан диск.
Задача 2.8. Дан прямоугольник на плоскости (предположим, что он эластичен, т. е. может растягиваться и менять свою площадь). Выдавить из него букву Я. Использовать B -поверхность.
Задача 2.9. Дан диск. Берем ручку, т. е. цилиндр, и приклеиваем два конца ручки к одной стороне диска. Изобразить деформацию диска, дающую тор, из которого вырезан диск.
Задача 2.10. Склеить тор (бутылку Клейна, проективную плоскость) из четырех треугольников, с помощью треугольной поверхности, т. е. задать восемь кривых, на которые натянутся треугольники для образования соответствующей поверхности.
Задача 2.11. Дана поверхность Безье, гомеоморфная диску. С помощью операции деления поверхности вырезать букву П.
Задача 2.12. Нарисуйте на плоскости случайный ориентированный (реберно) взвешенный граф со случайными положительными весами. Визуализируйте веса как метки ребер. Предусмотрите возможность менять количество вершин и вероятность появления ребра. Интерпретируя веса как пропускные способности соответствующих ребер-соединений, визуализируйте путь максимальной пропускной способности между заданными вершинами. (Пропускная способность маршрута равна минимальному весу входящего в него ребра. Таким образом, нужно найти маршрут с максимальным весом минимального ребра.) Предусмотрите возможность динамического выбора вершин.
Задача 2.13. Напомним, что графом Кэли группы G для системы ее образующих 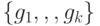 называется ориентированный граф, множество вершин которого совпадает с G, и ребро с меткой
называется ориентированный граф, множество вершин которого совпадает с G, и ребро с меткой  идет из вершины
идет из вершины  в вершину
в вершину  , если и только если
, если и только если 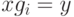 . Обычно при визуализации ребра, соответствующие разным образующим, изображают разными цветами. Напомним, что свободным произведением двух групп
. Обычно при визуализации ребра, соответствующие разным образующим, изображают разными цветами. Напомним, что свободным произведением двух групп 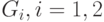 , заданных наборами образующих
, заданных наборами образующих 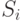 и наборами соотношений
и наборами соотношений 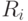 , называется группа с набором образующих
, называется группа с набором образующих 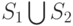 и набором соотношений
и набором соотношений  . Визуализировать граф Кэли для свободного произведения циклических групп
. Визуализировать граф Кэли для свободного произведения циклических групп 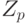 и
и 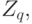 заданных в виде
заданных в виде  и
и 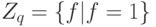 . Предусмотреть возможность выбора разных
. Предусмотреть возможность выбора разных  и
и  . Расположить нейтральный элемент в центре, предусмотреть динамический выбор числа видимых уровней.
. Расположить нейтральный элемент в центре, предусмотреть динамический выбор числа видимых уровней.
 -метрика на плоскости порождается так называемой
-метрика на плоскости порождается так называемой  -нормой, единичная окружность которой представляет собой правильный
-нормой, единичная окружность которой представляет собой правильный 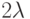 -угольник. Визуализировать минимальное остовное дерево, соединяющее данные точки плоскости с
-угольник. Визуализировать минимальное остовное дерево, соединяющее данные точки плоскости с  -метрикой. Точки задавать локаторами. Предусмотреть возможность добавлять и удалять точки, а также изменять
-метрикой. Точки задавать локаторами. Предусмотреть возможность добавлять и удалять точки, а также изменять  . Задача 2.17. Визуализировать минимальное остовное дерево, соединяющее данные точки трехмерного пространства. Точки задавать трехмерными локаторами. Предусмотреть возможность задавать количество точек. Задача 2.18. Визуализировать разбиение случайного множества точек в пространстве на кластеры с помощью компонент графа ближайших соседей. Раскрасить компоненты в разные цвета. Предусмотреть возможность выбора разных функций расстояния:
. Задача 2.17. Визуализировать минимальное остовное дерево, соединяющее данные точки трехмерного пространства. Точки задавать трехмерными локаторами. Предусмотреть возможность задавать количество точек. Задача 2.18. Визуализировать разбиение случайного множества точек в пространстве на кластеры с помощью компонент графа ближайших соседей. Раскрасить компоненты в разные цвета. Предусмотреть возможность выбора разных функций расстояния: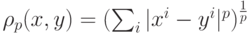
Предусмотреть возможность задавать количество точек.
Необходимые для решения следующих задач определения из тензорного анализа можно найти, например, в книге [12].
Задача 2.19. Реализовать функции опускания и поднятия индексов тензора произвольного типа. В качестве невырожденных тензоров типа (0,2) и (2,0) использовать или метрический тензор, если он задан, или тензор, указанный в необязательном аргументе. С помощью полученной функции реализовать оператор "звездочка Ходжа" (с заданной метрикой).
Задача 2.20. Реализовать операцию ковариантного дифференцирования тензорного поля произвольного типа. В качестве аффинной связности использовать или заданную, если она есть, или указанную в необязательном аргументе. С помощью полученной функции реализовать ковариантное дифференцирование вдоль векторного поля и запись уравнения геодезических.
Задача 2.21. Реализовать процедуру, задающую симплектическую структуру (невырожденную замкнутую 2-форму). С помощью нее реализовать операцию взятия косого градиента функции и вычисления скобки Пуассона функций на симплектическом многообразии. Проверить справедливость тождества Якоби для скобки Пуассона.
Задача 2.22. Написать уравнения параллельного переноса на плоскости Лобачевского в модели верхней полуплоскости, решить их численно и визуализировать возможность переноса вектора вдоль заданной кривой. Кривую задавать локаторами. Начальный вектор - динамически. Для фиксированной пары точек и кривой предусмотреть возможность вычислить матрицу оператора переноса.
Задача 2.23. Написать уравнения параллельного переноса на трехмерной сфере, решить их численно и визуализировать поведение нормальной плоскости к геодезической при параллельном переносе вдоль нее. В качестве модели использовать стереографическую проекцию. Предусмотреть возможность менять точку на геодезической. Для фиксированной пары точек предусмотреть возможность вычислить матрицу оператора переноса.
Задача 2.24. Написать уравнения геодезических в трехмерном пространстве Лобачевского в модели стереографической проекции, т. е. в трехмерном шаре и в модели в верхнем полупространстве. Визуализировать "все" геодезические, проходящие через динамически выбранную точку.
Задача 2.25. С помощью пакета Mathematica вывести формулы, выражающие существенную компоненту тензора кривизны двумерной поверхности только через компоненты ее метрического тензора и их производные. Проверить ответ для случая, когда поверхность задана графиком функции.
Задача 2.26. Реализовать процедуру вычисления скалярной кривизны двумерной поверхности в 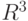 через компоненты тензора Римана римановой связности индуцированной метрики. Проверить на примерах конкретных поверхностей выполнение теоремы Гаусса о связи скалярной и гауссовых кривизн.
через компоненты тензора Римана римановой связности индуцированной метрики. Проверить на примерах конкретных поверхностей выполнение теоремы Гаусса о связи скалярной и гауссовых кривизн.
Задача 2.27. На матричной группе 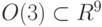 ортогональных
ортогональных  матриц ввести локальные координаты в окрестности единицы и записать в них индуцированную метрику, символы Кристоффеля и уравнения геодезических. Проверить, что
матриц ввести локальные координаты в окрестности единицы и записать в них индуцированную метрику, символы Кристоффеля и уравнения геодезических. Проверить, что 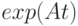 , где
, где  - кососимметрическая матрица, является решением полученной системы уравнений.
- кососимметрическая матрица, является решением полученной системы уравнений.