| Украина |
Первое знакомство с пакетом Mathematica
Выражения f[a,b,...]
Встроенные:
![\tt
In[27]:=Sin[$\pi$/2] \\ \\
Out[27]=1](/sites/default/files/tex_cache/77ac550daed522340f901b5b0050531b.png)
Создание выражений:
![\tt
In[28]:=f[x\_]:=x^2 \\ \\
In[29]:=\!f[2] \\
\phantom{In[29]:=}f[a] \\
\phantom{In[29]:=}f[Sin [x]]+f[Cos[x]] \\ \\
Out[29]=4 \\ \\
Out[30]=a^2 \\ \\
Out[31]=Cos[x]^2+Sin[x]^2](/sites/default/files/tex_cache/66083e2b9edda1107b0ee37ed98e2b90.png)
Значок 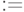 называется
называется  . Он отличается от значка
. Он отличается от значка  , который называется
, который называется  , тем, как осуществляется вычисление присвоенного выражения.
, тем, как осуществляется вычисление присвоенного выражения.  вычисляет правую часть
вычисляет правую часть  формулы
формулы 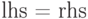 еще до присвоения и результат присваивает левой части
еще до присвоения и результат присваивает левой части  ;
;  присваивает левой части
присваивает левой части  невычисленную правую часть
невычисленную правую часть  , и при каждом вычислении левой части присвоенная правая часть вычисляется заново с использованием текущих значений связанных с
, и при каждом вычислении левой части присвоенная правая часть вычисляется заново с использованием текущих значений связанных с  объектов.
объектов.
Для примера используем функцию ![\text{Random[ ]}](/sites/default/files/tex_cache/23bfb20e616daff1a15825d10395dd14.png) , которая выдает случайное вещественное число в пределах между 0 и 1. В первом примере перед присвоением вычисляется некоторое случайное число и результат присваивается переменной
, которая выдает случайное вещественное число в пределах между 0 и 1. В первом примере перед присвоением вычисляется некоторое случайное число и результат присваивается переменной  , поэтому при каждом появлении
, поэтому при каждом появлении  заменяется на одно и то же присвоенное число. Во втором примере
заменяется на одно и то же присвоенное число. Во втором примере  присваивается неотработанная функция
присваивается неотработанная функция ![\text{Random[ ]}](/sites/default/files/tex_cache/23bfb20e616daff1a15825d10395dd14.png) , и при каждом появлении
, и при каждом появлении  эта функция вычисляется каждый раз заново, чем и объясняются разные результаты вычисления
эта функция вычисляется каждый раз заново, чем и объясняются разные результаты вычисления  .
.
![\tt
In[32]:=z=Random[] \\
\phantom{In[32]:=}\,z \\
\phantom{In[32]:=}\,z \\ \\
Out[32]=0.871538 \\ \\
Out[33]=0.871538 \\ \\
Out[34]=0.871538 \\ \\
In[35]:=z:=Random[] \\
\phantom{In[35]:=}\,z \\
\phantom{In[35]:=}\,z \\ \\
Out[36]=0.877299 \\ \\
Out[37]=0.620971 \\ \\
In[38]:=z=.](/sites/default/files/tex_cache/211781e72a5c6c82047b43fa81a799a1.png)
Еще один пример:
![\tt
In[39]:=y=2 \\ \\
Out[39]=2 \\ \\
In[40]:=f[y_]=y^3 \\ \\
Out[40]=8 \\ \\
In[41]:=g[y_]:=y^3 \\ \\
In[42]:=f[w] \\
\phantom{In[42]:=}\,g[w] \\ \\
Out[42]=8 \\ \\
Out[43]=w^3 \\ \\
In[44]:=y=.](/sites/default/files/tex_cache/ea0fb76e8c48673ebe0ea0a9f4422f3b.png)
Чтобы очистить сделанное присвоение вида f[x_] = rhs или f[x_] := rhs, выполните команду Clear[f]
![\tt
In[45]=Clear[f] \\
\phantom{In[45]=}\,Clear[g] \\ \\
In[47]:=f[x] \\
\phantom{In[47]:=}\,g[x] \\ \\
Out[47]=f[x] \\ \\
Out[48]=g[x]](/sites/default/files/tex_cache/74bc3cc9872c6e23d96f8670d3e9ee4b.png)
Для одновременной очистки нескольких присвоений, сделанных для 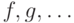 , можно использовать
, можно использовать ![\text{\tt Clear[f, g, \ldots]}](/sites/default/files/tex_cache/6e6f616dd09ad59fa1c7656454571537.png) :
:
![\tt
In[49]:=f[x\_]:=x^2 \\
\phantom{In[49]:=}\,g[x\_]:x^3 \\
\phantom{In[49]:=}\,f[x] \\
\phantom{In[49]:=}\,g[x] \\ \\
Out[51]=x^2 \\ \\
Out[52]=x^3 \\ \\
In[53]:=Clear[f,g] \\
\phantom{In[53]:=}\,f[x] \\
\phantom{In[53]:=}\,g[x] \\ \\
Out[54]=f[x] \\ \\
Out[55]=g[x]](/sites/default/files/tex_cache/f5e8f4b9e675e1fa1ecf2a34c2cc6ce4.png)
Некоторые другие способы записи выражений f[x]
![\tt
In[56]:=f[x\_]:=x^2 \\
\phantom{In[56]:=}\,g[x\_, y\_]:=xy^2](/sites/default/files/tex_cache/4f2650c08ee0dab37653ed532d2aab12.png)
В приведенных ниже первых трех примерах вычисляется значение функции  на переменной
на переменной 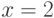 ; в четвертом примере вычисляется значение функции
; в четвертом примере вычисляется значение функции  на переменных
на переменных 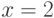 и
и  .
.
![\tt
In[56]:=f[2] (*Standard форма*) \\
\phantom{In[56]:=}\,f@2 (*Prefix форма*) \\
\phantom{In[56]:=}\,2//f (* Postfix форма*) \\
\phantom{In[56]:=}\,2 \sim g \sim 3 (* Infix форма*) \\ \\
Out[58]=4 \\ \\
Out[59]=4 \\ \\
Out[60]=4 \\ \\
Out[61]=18 \\ \\
In[62]:= Clear[f,g]](/sites/default/files/tex_cache/684af531604a778fb252bafe747f1c12.png)
Задание функции непосредственно, без присвоения и имени (безымянные функции, pure functions)
В приводимых ниже примерах значок  используется для обозначения единственной переменной задаваемой функции, значки
используется для обозначения единственной переменной задаваемой функции, значки 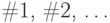 .- соответственно первая, вторая и т. д. переменные для функции многих переменных; значок
.- соответственно первая, вторая и т. д. переменные для функции многих переменных; значок  ставится после описания функции и обозначает, что стоящее слева от него выражение надо рассматривать как определение функции, а все вместе с ним - как саму функцию.
ставится после описания функции и обозначает, что стоящее слева от него выражение надо рассматривать как определение функции, а все вместе с ним - как саму функцию.
![\tt
In[63]:= (\#^2+2) \& [x] \\ \\
Out[63]=2+x^2 \\ \\
In[64]:= (\#1^2 +\#2^4) \& [x,y] \\ \\
Out[64]=x^2+y^4 \\ \\
In[65]:= f=(\#^2+2) \& \\ \\
Out[65]=\#1^2+2 \& \\ \\
In[66]:= f[x] \\ \\
Out[66]=2+x^2 \\ \\
In[67]:= Clear[f]](/sites/default/files/tex_cache/b40669f15aede1aada8b5f3ca57b3d77.png)
Подавление вывода результата и расположение команд внутри одной клетки
Если после команды ставится точка с запятой 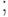 , то вывод результата не происходит:
, то вывод результата не происходит:
![\tt
In[68] = 2 + 2 \\ \\
Out[68]=4 \\ \\
In[69]:= 2+2;](/sites/default/files/tex_cache/69636ca4e20a25eb55d629fbdcef998b.png)
На одной строке можно писать сразу несколько команд, разделяя их 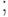 (выводы результатов этих команд производиться не будут); можно писать одну команду сразу на нескольких строках:
(выводы результатов этих команд производиться не будут); можно писать одну команду сразу на нескольких строках:
![\tt
In[70]:=f[x\_]:=x^2; g[x\_, y\_]:=x^2+y^3; h[x\_, y\_]:= \\
\phantom{In[70]:=f}3xy; \\ \\
In[71]:=f[a] \\
\phantom{In[71]:=}\;g[b,c] \\
\phantom{In[71]:=}\;h[d,e] \\ \\
Out[71]=a^2 \\ \\
Out[72]= b^2+c^3 \\ \\
Out[73]=3de \\ \\
In[74]:= Clear[f,g,h]](/sites/default/files/tex_cache/e4875d6b49d07d80f6a79f52a3e0d7aa.png)
Списки List[x,y,...] или {x,y,...}
![\tt
In[75]:= \{x,\{a,b\},z\} \\ \\
Out[75]=\{x, \{a,b\}, z\}](/sites/default/files/tex_cache/ec3ba07e54aca2743d3deee2c8481ce7.png)
Доступ к элементам списка (команда Part или [[ ...]])
![\tt
In[76]:=\{x, \{a,b\}, z\} [[3]] \\
\phantom{In[76]:=}\;Part[\{x, \{a,b\}, z\}, 3] \\ \\
Out[76]=z \\ \\
Out[77]=z \\ \\
In[78]:= \{x, \{a,b\},z\} [[2,1]] \\
\phantom{In[78]:=}\;Part[\{x, \{a,b\},z\},2,1] \\ \\
Out[78]=a \\ \\
Out[79]=a \\ \\
In[80]:= \{x,\{a,b\},z\} [[\{1,3,1,2,3,3\}]] \\ \\
Out[80]=\{x,z,x,\{a,b\},z,z\} \\ \\
In[81]:=\{1,2,3,4,5,6,7\}[[2;;5]] \\ \\
Out[81]=\{2,3,4,5\}](/sites/default/files/tex_cache/856a7c6dfa2b05eae1123ef2ffeaeea4.png)
Вместо скобок [[ и ]] удобно использовать [[ и ]]
Они получаются набором  и
и ![\text{\fbox{Esc} ]] \fbox{Esc}}](/sites/default/files/tex_cache/ada9c39fee861e7c0bd77e9bf16aafeb.png) соответственно:
соответственно:
![\tt
In[82]:= \{x,\{a,b\},z\}[\![3]\!] \\ \\
Out[82]=z](/sites/default/files/tex_cache/a18f59f5ce47564d5b4f4469f39466fb.png)
Арифметические операции над списками - покомпонентные
![\tt
In[83]:= \{1,2,3\}+\{x,y,z\} \\ \\
Out[83]=\{1+x, 2+y, 3+z\} \\ \\
In[84]:= \{1,2,3\}x\} \\ \\
Out[84]=\{x, 2x, 3x\} \\ \\
In[85]:= \{1,2,3\}\{x,y,z\} \\ \\
Out[85]=\{x,2y, 3z\} \\ \\
In[86]:= \{1,2,3\}/\{x,y,z\}\} \\ \\
Out[86]=\left \{\frac 1x, \frac 2y, \frac 3z \right \}](/sites/default/files/tex_cache/1e3aecd8ddea09c8ad20e49b8c0c1880.png)
