|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Лекция 4: Показатель размытости нечетких множеств. Нечеткие меры и интегралы
Нечеткие интегралы
Определение. Нечеткий
интеграл от функции ![h\colon X\to [0,1]](/sites/default/files/tex_cache/8fd5664e5116139cdef5d2cbe77da1d0.png) на множестве
на множестве 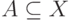 по нечеткой мере
по нечеткой мере  определяется как
определяется как
![\int\limits_A {h(x) \circ g} = \mathop {\sup
}\limits_{\alpha \in [0,1]} \;\left( {\alpha \wedge g(A \cap H_\alpha )}
\right),](/sites/default/files/tex_cache/8d9a67f55777451f92b924e2493a7a5a.png)
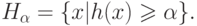
нечеткий интеграл принято также называть нечетким ожиданием.
Определение. Нечеткий
интеграл от функции ![h\colon X\to [0,1]](/sites/default/files/tex_cache/8fd5664e5116139cdef5d2cbe77da1d0.png) на нечетком
множестве
на нечетком
множестве 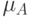 по нечеткой мере
по нечеткой мере  определяется как
определяется как
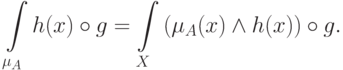
Для описания различных видов неопределенности в теории нечетких мер
используется общее понятие "степень нечеткости". В общем случае
оно включает в себя "степень важности", "степень
уверенности" и как отдельный
случай - "степень принадлежности" в теории нечетких множеств. Нечеткая
мера, таким образом, может интерпретироваться
различными способами в зависимости от конкретного применения. Пусть необходимо
оценить степень принадлежности некоторого элемента  множеству
множеству  .
Очевидно, что для пустого множества эта степень принадлежности равна
.
Очевидно, что для пустого множества эта степень принадлежности равна  , а для
, а для  (
(  ) равна
) равна  , т.е. степень принадлежности
для
, т.е. степень принадлежности
для  будет больше,
чем для
будет больше,
чем для 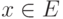 , если
, если  . Если степень
принадлежности
. Если степень
принадлежности  равна
равна  ,
а вместо
,
а вместо  задано нечеткое подмножество
задано нечеткое подмножество 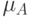 , то
, то
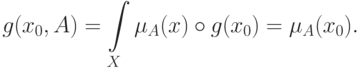
Это говорит о том, что степень нечеткости суждения " 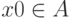 "
равна степени принадлежности
"
равна степени принадлежности  нечеткому подмножеству
нечеткому подмножеству 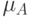 .
Таким образом, понятие степени нечеткости в теории нечетких мер включает
в себя понятие степени принадлежности теории нечетких множеств.
.
Таким образом, понятие степени нечеткости в теории нечетких мер включает
в себя понятие степени принадлежности теории нечетких множеств.
Применение нечетких мер и интегралов для решения слабо структурированных задач
Процесс субъективного оценивания
Рассмотрим задачу субъективного оценивания некоторым индивидом нечетко
описываемых объектов, таких как дом, лицо и т.п. Предположим, что объект
характеризуется  показателями.
показателями.
Пусть 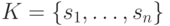 — множество показателей.
При оценивании
дома такими показателями могут быть:
— множество показателей.
При оценивании
дома такими показателями могут быть:  — площадь,
— площадь, 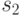 — удобства и т.д.
В общем случае множество
— удобства и т.д.
В общем случае множество  не обязательно должно быть множеством
физических
показателей, оно может быть множеством мнений, критериев и т.п.
не обязательно должно быть множеством
физических
показателей, оно может быть множеством мнений, критериев и т.п.
Пусть ![h\colon K\to [0,1]](/sites/default/files/tex_cache/aef8861e1cdc0d2964f5eb6ca7ae0d7f.png) — частная оценка объекта, т.е.
— частная оценка объекта, т.е. 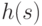 — оценка
элемента
— оценка
элемента  . Если речь идет о распознавании образов, то
. Если речь идет о распознавании образов, то 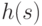 может
рассматриваться как характеристическая функция образа. На практике
может
рассматриваться как характеристическая функция образа. На практике 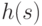 может быть легко определена объективно или субъективно. Например, когда
объект — дом, объективно имеем оценку
может быть легко определена объективно или субъективно. Например, когда
объект — дом, объективно имеем оценку  ,
которая может быть нормализована числом из интервала
,
которая может быть нормализована числом из интервала ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) .
.
Предположим, что нечеткая мера для  является субъективной мерой,
выражающей степень важности подмножества из
является субъективной мерой,
выражающей степень важности подмножества из  . Например,
. Например, 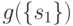 выражает
степень важности элемента
выражает
степень важности элемента  при оценке объекта,
при оценке объекта,  —
аналогично обозначает степень важности показателей
—
аналогично обозначает степень важности показателей  и
и 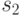 .
Необходимо отметить, что степень важности всего множества
.
Необходимо отметить, что степень важности всего множества  равна
единице.
равна
единице.
Вычисляя нечеткий интеграл от  до
до  , получаем
, получаем
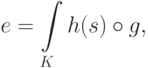
 — обобщенная оценка объекта.
— обобщенная оценка объекта.Данное уравнение представляет собой свертку  частных оценок.
Линейный обобщенный критерий используется обычно в том случае,
когда отдельные показатели взаимно независимы. Свертка же может
быть очень полезной, когда существует взаимозависимость показателей, что
характерно для большинства задач выбора в нечеткой среде.
частных оценок.
Линейный обобщенный критерий используется обычно в том случае,
когда отдельные показатели взаимно независимы. Свертка же может
быть очень полезной, когда существует взаимозависимость показателей, что
характерно для большинства задач выбора в нечеткой среде.
Экспериментальное определение нечеткой меры
Рассмотрим метод приближенного экспериментального определения нечеткой меры.
Предположим, что существует  объектов.
Пусть
объектов.
Пусть ![\(h_j :K \to [0,1]\)](/sites/default/files/tex_cache/758aed7c72487fe33570eec75bf2a15b.png) — частная оценка
— частная оценка  -го объекта,
а
-го объекта,
а 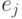 — общая оценка. Предъявляя индивиду объекты и их
частные
оценки, можно получить его субъективные оценки
— общая оценка. Предъявляя индивиду объекты и их
частные
оценки, можно получить его субъективные оценки 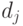 из интервала
из интервала ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) для всех объектов.
для всех объектов.
Обозначим  и аналогично
и аналогично  . Производя
нормализацию
. Производя
нормализацию 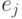 , мы имеем
, мы имеем
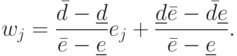
Субъективная нечеткая мера может быть получена при условии минимума критерия
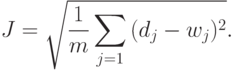
Впервые нечеткие меры применялись для оценки сходства одномерных образов. Например, рассматривалось решение задачи оценки домов. При этом дома оценивались по следующим пяти показателям: площадь, удобства и обстановка, окружающая среда, стоимость, время, требуемое на дорогу до места работы. Известны применения нечетких мер для оценки привлекательности экскурсионных районов, которые оценивались по таким показателям, как красота природы, архитектурные памятники и т.п. Результаты оценок использовались для прогнозирования числа экскурсий в ближайшие десять лет.
