НОУ ИНТУИТ | Основы теории нечетких множеств. Лекция 2: Нечеткие отношения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 26.07.2006 | Уровень: специалист | Доступ: платный

|

Вам нравится? Нравится 36 студентам

| Поделиться |

Поддержать программу

Свойства нечетких отношений

Различные типы нечетких отношений определяются с помощью свойств, аналогичных свойствам обычных отношений, причем для нечетких отношений можно указать различные способы обобщения этих свойств.

1. Рефлексивность:

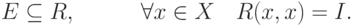
$E \subseteq R,\quad \quad \quad \forall x \in X\quad R(x,x) = I .$

2. Слабая рефлексивность:

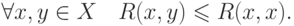
$\forall x,y \in X\quad R(x,y) \leqslant R(x,x) .$

3. Сильная рефлексивность:

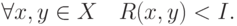
$\forall x,y \in X\quad R(x,y) < I .$

4. Антирефлексивность:

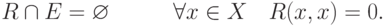
$R \cap E = \varnothing \quad \quad \quad \forall x \in X\quad R(x,x) = 0 .$

5. Слабая антирефлексивность:

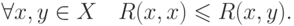
$\forall x,y \in X\quad R(x,x) \leqslant R(x,y) .$

6. Сильная антирефлексивность:

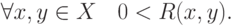
$\forall x,y \in X\quad 0 < R(x,y) .$

7. Симметричность:

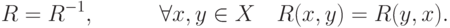
$R = R^{ - 1} ,\quad \quad \quad \forall x,y \in X\quad R(x,y) = R(y,x) .$

8. Антисимметричность:

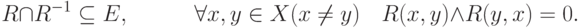
$R \cap R^{ - 1} \subseteq E,\quad \quad \quad \forall x,y \in X(x \ne y)\quad R(x,y) \wedge R(y,x) = 0 .$

9. Асимметричность:

$R \cap R^{ - 1} = \varnothing ,\quad \quad \quad \forall x,y \in X\quad R(x,y) \wedge R(y,x) = 0 .$

10. Сильная линейность:

$R \cup R^{ - 1} = U,\quad \quad \quad \forall x,y \in X\quad R(x,y) \vee R(y,x) = I .$

11. Слабая линейность:

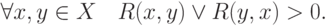
$\forall x,y \in X\quad R(x,y) \vee R(y,x) > 0 .$

12. Транзитивность:

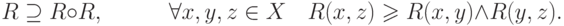
$R \supseteq R \circ R,\quad \quad \quad \forall x,y,z \in X\quad R(x,z) \geqslant R(x,y) \wedge R(y,z) .$

Декомпозиция нечетких отношений

Одно из важнейших свойств нечетких отношений заключается в том, что они могут быть представлены в виде совокупности обычных отношений, причем могут быть упорядочены по включению, представляя собой иерархическую совокупность отношений. Разложение нечеткого отношения на совокупность обыкновенных отношений основано на понятии $\alpha$ -уровня нечеткого отношения. Здесь для простоты будем полагать, что линейно упорядочено.

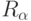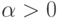$\alpha$ -уровнем нечеткого отношения называется обычное отношение $R_\alpha$ , определяемое для всех $\alpha>0$ следующим образом:

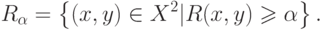
$R_\alpha = \left\{ {(x,y) \in X^2 |R(x,y) \geqslant \alpha } \right\} .$

Очевидно, что $\alpha$ -уровни нечетких отношений удовлетворяют соотношению:

$\alpha \leqslant \beta \quad \Rightarrow \quad R_\alpha \supseteq R_\beta ,$

представляя собой совокупность вложенных друг в друга отношений.

Теорема. Нечеткое отношение обладает каким-либо свойством из перечисленных (кроме сильной рефлексивности, сильной антирефлексивности, слабой линейности) тогда и только тогда, если этим свойством обладают все его $\alpha$ -уровни.

Эта теорема играет важную роль в теории нечетких отношений. Во-первых, она показывает, что основные типы обычных отношений и их свойства могут быть обобщены и на случай нечетких отношений, и приводит ясный способ такого обобщения. Во-вторых, оказывается, что основные типы нечетких отношений могут быть представлены как совокупность, иерархия обычных отношений того же типа. И если решением практической задачи является получение на множестве некоторого отношения заданного типа, например эквивалентности или порядка, то построение на соответствующего нечеткое отношение позволяет получать сразу ансамбль необходимых обычных отношений, а это дает возможность учитывать неоднозначность решений, присущих практическим ситуациям, и предоставляет лицу, принимающему решение, некоторую свободу выбора. В-третьих, теория нечетких множеств, допуская подобную неоднозначность возможных решений, ограничений и целей, дает возможность оперировать сразу всей совокупностью таких объектов как единым целым.

Нечеткое отношение может быть представлено в следующем виде:

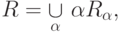
$R = \mathop \cup \limits_\alpha \,\alpha R_\alpha ,$

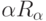где отношения $\alpha R_\alpha$ определяются следующим образом: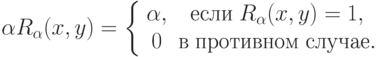

$\alpha R_\alpha (x,y) = \left\{ {\begin{array}{*{20}c} {\alpha ,} & {\t{\char229}\t{\char241}\t{\char235}\t{\char232}\;R_\alpha (x,y) = 1,} \\ 0 & {\t{\char226}\;\t{\char239}\t{\char240}\t{\char238}\t{\char242}\t{\char232}\t{\char226}\t{\char237}\t{\char238}\t{\char236}\;\t{\char241}\t{\char235}\t{\char243}\t{\char247}\t{\char224}\t{\char229}.} \\ \end{array} } \right.$

Кроме всех вышеописанных свойств, выполняющихся для всех $\alpha$ -уровней, могут быть определены аналогичные свойства, выполняющиеся только для одного или нескольких $\alpha$ -уровней. Приведем примеры таких $\alpha$ -свойств, предполагая, что элемент $\alpha$ фиксированный:

$\alpha$ -симметричность

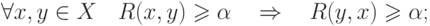
$\forall x,y \in X\quad R(x,y) \geqslant \alpha \quad \Rightarrow \quad R(y,x) \geqslant \alpha ;$

$\alpha$ -транзитивность

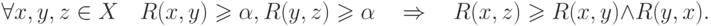
$\forall x,y,z \in X\quad R(x,y) \geqslant \alpha ,R(y,z) \geqslant \alpha \quad \Rightarrow \quad R(x,z) \geqslant R(x,y) \wedge R(y,x) .$

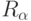Аналогично могут быть определены и другие $\alpha$ -свойства. Они могут рассматриваться в задачах, в которых вводится порог на силу отношения либо ищется такое $\alpha$ , при котором $R_\alpha$ обладает требуемым свойством.

Дальше >>

Основы теории нечетких множеств

Основы теории нечетких множеств

Нечеткие отношения

Свойства нечетких отношений

Декомпозиция нечетких отношений

Вопросы и ответы

Студенты

Авторизоваться

Основы теории нечетких множеств

Основы теории нечетких множеств

Нечеткие отношения

Свойства нечетких отношений

Декомпозиция нечетких отношений

Вопросы и ответы

Студенты