НОУ ИНТУИТ | Основы САПР. Лекция 15: Разработка математических моделей при проектировании технологии

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 13.03.2008 | Уровень: специалист | Доступ: платный

|

Вам нравится? Нравится 19 студентам

| Поделиться |

Поддержать программу

Аннотация: Рассматривается методология построения математических моделей при проектировании технологии производства РЭС. Цель лекции: изложить методологию, знание которой является обязательным при проектировании технологии изготовления любой промышленной продукции, в частности, РЭС

Ключевые слова: моделирование, операции, определение, САПР, теоретические методы, экспериментальные методы, макромоделирование, пассивный эксперимент, активный эксперимент, макромодель, внешние параметры, метод наименьших квадратов, оценка математического ожидания, коэффициент регрессии, координаты, фазовые переменные, алгебраизация, метод конечных разностей (МКР), метод конечных элементов (МКЭ), пользователь, математическая модель элемента, объединение, коэффициенты, потенциал, знание, компонентные уравнения, теоретический метод

15.1. Методы получения моделей элементов

Получение моделей элементов (моделирование элементов) в общем случае — процедура неформализованная. Основные решения, касающиеся выбора вида математических соотношений, характера используемых переменных и параметров, принимает проектировщик. В то же время такие операции, как расчет численных значений параметров модели, определение областей адекватности и др., алгоритмизированы и решаются на ЭВМ. Поэтому моделирование элементов обычно выполняется специалистами конкретных технических областей с помощью традиционных средств экспериментальных исследований и средств САПР.

Методы получения функциональных моделей элементов делят на теоретические и экспериментальные. Теоретические методы основаны на изучении физических закономерностей, протекающих в объекте процессов. Далее происходит определение соответствующего этим закономерностям математического описания, обоснование и принятие упрощающих предположений, выполнение необходимых выкладок и приведение результата к принятой форме представления модели. Экспериментальные методы основаны на использовании внешних проявлений свойств объекта, фиксируемых во время эксплуатации однотипных объектов или при проведении целенаправленных экспериментов.

Несмотря на эвристический характер многих операций моделирования, имеется ряд положений и приемов, общих для получения моделей различных объектов. Достаточно общий характер имеют методика макромоделирования, математические методы планирования экспериментов, а также алгоритмы формализуемых операций расчета численных значений параметров и определения областей адекватности.

15.1.1. Методика макромоделирования

Применение методики состоит из следующих этапов:

Определение тех свойств объекта, которые должны отражаться моделью (устанавливаются требования к степени универсальности будущей модели).
Сбор априорной информации о свойствах моделируемого объекта. Примерами собираемых сведений могут служить справочные данные, математические модели и результаты эксплуатации существующих аналогичных объектов и т. п. Назовем эту информацию производственной статистикой.
Получение общего вида уравнений модели (структуры модели). Этот этап в случае теоретических методов включает выполнение всех присущих этим методам операций, перечисленных выше. Часто проектировщику модели удобнее оперировать не уравнениями, а эквивалентными схемами, с помощью которых инженеру проще устанавливать физический смысл различных элементов математической модели.
Определение численных значений параметров модели. Возможны следующие приемы выполнения этого этапа:
- использование специфических расчетных соотношений с учетом собранных на этапе 2 сведений;
- решение экстремальной задачи, в которой в качестве целевой функции выбирается степень совпадения известных значений выходных параметров объекта с результатами использования модели, а управляемыми параметрами являются параметры модели;
- проведение экспериментов и обработка полученных результатов.
Оценка точности полученной модели и определение области ее адекватности. При неудовлетворительной точности оценок выполняют итерационное приближение к желаемому результату повторением этапов 3-5.
Представление полученной модели в форме, принятой в используемой библиотеке моделей.

15.1.2. Методы планирования экспериментов

Для целей моделирования используют пассивные и активные эксперименты. В пассивных экспериментах нет возможности выбирать условия опыта по своему усмотрению и устанавливать значения факторов на желаемом уровне. В активных экспериментах опыты проводятся по заранее разработанному плану, выражающему количество опытов и значения факторов в каждом опыте [28, 31].

Выбор вида зависимости выходного параметра макромодели у (в общем случае рассматривается вектор выходных параметров Y ) от внешних параметров q_k, объединенных в вектор факторов Q, осуществляется проектировщиком. Чаще всего в методах планирования эксперимента используются модели линейные

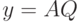( 15.1)

или квадратичные

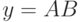( 15.2)

где А — вектор — строка коэффициентов (параметров) модели; В — вектор, включающий факторы q_k, те или иные произведения из двух, трех или более факторов и, возможно, также квадраты факторов q_k; k = 1, ..., р; р — число факторов.

Число опытов N, как правило, должно превышать число определяемых параметров вектора А. Параметры рассчитывают по методу наименьших квадратов, т. е. из условия минимизации суммы квадратов отклонений значений $\tilde y_\ell$ , определенных по уравнению модели (15.1), и измеренных значений $y_\ell$ :

$min\sum\limits_{\ell=1}^N {\left(\tilde y_\ell(A)-y_\ell)\right}^2$

( 15.3)

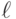где $\ell$ — номер опыта.

В зависимости от способов планирования преимущества активных экспериментов перед пассивными могут выражаться в получении оптимального положения области адекватности, в ее увеличенном объеме, в упрощении оценок точности и т. п.

15.1.3. Регрессионный анализ

Связь между у и Q может быть не функциональной, а статистической, что особенно характерно при пассивных экспериментах. Для получения моделей в такой ситуации часто применяют регрессионный анализ. Модель создается в форме уравнения регрессии (15.1), в котором роль коэффициентов a_k в векторе А выполняют коэффициенты относительной регрессии.

Рассмотрим алгоритм вычисления коэффициентов a_k. По результатам пассивных экспериментов получаются оценки математических ожиданий М_у, М_к1 среднеквадратичных отклонений 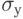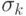$\sigma _{у}$ , $\sigma _{k}$ , соответственно, для выходного у и внешних q_k параметров, а также коэффициенты корреляции r_k между у и q_k, образующие вектор R, и коэффициенты корреляции d_kj между факторами q_k и q_j, образующие матрицу D. Далее решается система линейных алгебраических уравнений

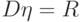$D\eta=R$

( 15.4)

и полученный вектор 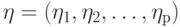$\eta = (\eta _{1}, \eta _{2}, \dots , \eta _{р})$ используется при расчете относительных коэффициентов регрессии по формуле

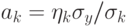$a_k=\eta_k \sigma_y/ \sigma_k$

( 15.5)

Если факторы q_k некоррелированы, то D — единичная матрица и можно обойтись без решения системы (15.4), так как $\eta _{к} = r_{k}$ .

15.1.4. Диалоговое моделирование

Поскольку в методике макромоделирования присутствуют эвристические и формальные операции, целесообразно разрабатывать модели элементов в диалоговом режиме работы с ЭВМ. Используемый язык взаимодействия человека с ЭВМ должен иметь возможность оперативного ввода исходной информации о структуре модели, об известных характеристиках и параметрах объекта, о плане экспериментов. Диалоговое моделирование должно иметь программное обеспечение, в котором реализованы алгоритмы статистической обработки результатов экспериментов. В данное программное обеспечение должен входить расчет выходных параметров эталонных моделей и создаваемых макромоделей, в том числе расчет параметров по методам планирования экспериментов и регрессионного анализа. В методику должны быть включены алгоритмы методов поиска экстремума, расчета областей адекватности и др. Пользователь, разрабатывающий модель, может менять уравнения модели, задавать их в аналитической, схемной или табличной форме, обращаться к нужным подпрограммам и тем самым оценивать результаты предпринимаемых действий, приближаясь к получению модели с требуемыми свойствами.

15.2. Математические модели объектов проектирования на микроуровне

Математические модели деталей и процессов на микроуровне отражают физические процессы, протекающие в сплошных средах и непрерывном времени. Независимыми переменными в этих моделях являются пространственные координаты и время. В качестве зависимых переменных выступают фазовые переменные, такие как потенциалы, напряженности полей, концентрации частиц, деформации и т. п. Взаимосвязи переменных выражаются с помощью уравнений математической физики — интегральных, интегро-дифференциальных или дифференциальных уравнений в частных производных. Эти уравнения составляют основу ММ на микроуровне.

Для получения законченной математической модели, используемой в задачах проектирования, необходимо дополнительно выполнить ряд процедур:

выбрать краевые условия. Краевые условия представляют собой сведения о значениях фазовых переменных и (или) их производных на границах рассматриваемых пространственных и временных областей;
дискретизировать задачу. Дискретизация подразумевает разделение рассматриваемых пространственных и временных областей на конечное число элементарных участков с представлением фазовых переменных конечным числом значений в избранных узловых точках, принадлежащих элементарным участкам;
алгебраизировать задачу — аппроксимировать дифференциальные и интегральные уравнения алгебраическими.

Используют два основных подхода к дискретизации и алгебраизации краевых задач, составляющие сущность методов конечных разностей (МКР) и конечных элементов (МКЭ). С помощью любого из этих методов формируется окончательная модель, исследуемая при выполнении различных процедур анализа проектируемого объекта.

Пользователь САПР средствами входного языка задает исходную информацию о конфигурации проектируемого объекта, о способе дискретизации — разделения среды на элементы, — о физических свойствах участков среды. Формирование модели объекта, т. е. разделение среды на элементы, выбор математических моделей элементов из заранее составленных библиотек, объединение моделей элементов в общую систему уравнений, так же как и решение получающихся уравнений, осуществляется автоматически на ЭВМ.

Основные уравнения математической физики, используемые в моделях проектируемых объектов. Процессы, протекающие в техническом объекте при его функционировании, по своей физической природе могут быть разделены на:

электрические;
тепловые;
магнитные;
оптические;
механические;
гидравлические и т. п.

Каждому типу процессов в математической модели соответствует своя подсистема, основанная на определенных уравнениях математической физики. Рассмотрим примеры уравнений, составляющих основу математических моделей технических объектов на микроуровне.

Электрические процессы в современных полупроводниковых приборах с достаточной точностью удается описать с помощью уравнений непрерывности и Пуассона. Уравнения непрерывности выражают скорости изменения концентраций свободных носителей заряда и записываются отдельно для дырок и электронов:

$\frac{\partial p}{\partial t}=\frac 1 q - div J_p + g_p$

( 15.6)

$\frac{\partial n}{\partial t}=\frac 1 q - div J_n + g_n$

( 15.7)

где p и n — концентрации дырок и электронов, соответственно; q — заряд электрона; g_P и g_n — скорости процесса генерации-рекомбинации, соответственно, дырок и электронов;

$J_p=q(-\mu_p p grad\varphi-D_p grad p);$

( 15.8)

$J_n=q(-\mu_n n grad\varphi-D_n grad p)$

( 15.9)

где q — плотности дырочного и электронного токов; 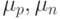$\mu _{p}, \mu _{n}$ — подвижности; D_p, D_n — коэффициенты диффузии дырок и электронов; $\phi$ — электрический потенциал.

Уравнения (15.8)-(15.9) показывают, что причинами изменения концентрации носителей могут быть неодинаковость числа носителей, втекающих (и вытекающих) в элементарный объем полупроводника (тогда 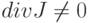$div J\ne 0$ ), и нарушение равновесия между процессами генерации и рекомбинации носителей. Уравнения (15.8) и (15.9), называемые уравнениями плотности тока, характеризуют причины протекания электрического тока в полупроводнике: электрический дрейф под воздействием электрического поля ( 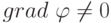$grad \ \varphi \ne 0$ ) и диффузию носителей при наличии градиента концентрации. Уравнение Пуассона характеризует зависимость изменений в пространстве напряженности электрического поля $Е = –grad \ \varphi$ от распределения плотности электрических зарядов $\rho$ :

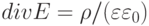$divE = \rho/ (\varepsilon\varepsilon_0)$

( 15.10)

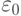где $\varepsilon$ — относительная диэлектрическая проницаемость среды; $\varepsilon _{0}$ — диэлектрическая постоянная.

В качестве краевых условий в моделях полупроводниковых приборов используют зависимости потенциалов на контактах от времени, принимают значения концентраций носителей на границе между внешним выводом и полупроводником равными равновесным концентрациям р_о и n₀, для границ раздела полупроводника и окисла задаются скоростью поверхностной рекомбинации g_S, что определяет величины нормальных к поверхности раздела составляющих плотностей тока J_p и J_n и т. д.

Результат решения уравнений непрерывности и Пуассона при известных краевых условиях — это поля потенциала и концентраций подвижных носителей в различных областях полупроводниковой структуры. Знание этих полей позволяет оценить электрические параметры прибора.

В основе моделей диффузионных процессов, используемых, в частности, для описания технологических операций диффузии примесей при изготовлений интегральных схем и полупроводниковых приборов, лежит уравнение диффузии

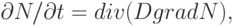$\partial N/ \partial t=div(D grad N),$

( 15.11)

где N — концентрация примеси; D — коэффициент диффузии.

Краевые условия представлены зависимостью распределения примеси N в объеме полупроводника в начальный момент времени и зависимостью поверхностной концентрации от времени.

На использовании закономерностей протекания тепловых процессов основано действие многих теплофизических установок. В РЭС полезные свойства обусловлены закономерностями электрических процессов, однако рассеяние мощности и изменения температуры оказывают заметное влияние на характер функционирования аппаратуры. Поэтому в моделях РЭС, как и в моделях многих устройств иной природы, приходится учитывать тепловые процессы. Теплоперенос в твердых телах описывается уравнением теплопроводности

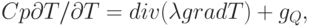$Cp\partial T/ \partial T=div(\lambda grad T)+g_Q,$

( 15.12)

где T — температура; С — удельная теплоемкость; р — плотность; $\lambda$ — коэффициент теплопроводности; g_Q — количество теплоты, выделяемой в единицу времени в единице объема.

Дальше >>

Основы САПР

Основы САПР