| Россия, г. Санкт-Петербург |
Математические модели (ММ) на различных иерархических уровнях
13.1. Иерархия математических моделей в САПР
Блочно-иерархический подход к проектированию радиоэлектронных средств (РЭС) включает в качестве своей основы иерархию математических моделей. Деление моделей по иерархическим уровням (уровням абстрагирования) происходит по степени детализации описываемых свойств и процессов, протекающих в объекте. При этом на каждом иерархическом уровне используют свои понятия "система" и "элементы". Так, система k -го уровня рассматривается как элемент на соседнем более высоком (k–1) -м уровне абстрагирования.
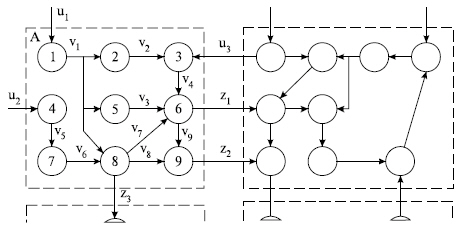
Представим структуру некоторого объекта в виде множества элементов ( рис. 13.1) и связей между ними.
Выделим в соответствии с блочно-иерархическим подходом в структуре объекта некоторые подмножества элементов и назовем их блоками (на рисунке показаны штриховыми линиями). Пусть состояние каждой связи характеризуется одной фазовой переменной vi, zj или uk. Здесь vi относится к внутренним связям между элементами данного блока, zj и uk относятся к выходам и входам блока соответственно.
Рассмотрим важные для функциональных моделей понятия полной модели и макромодели.
Полная модель блока есть модель, составленная из моделей элементов с учетом межэлементных связей, т. е. модель, описывающая как состояние выходов, так и состояние каждого из элементов блока. Моделями элементов блока А являются уравнения, связывающие входные и выходные переменные:
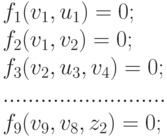 |
( 13.1) |
Полная модель блока есть система уравнений
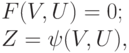 |
( 13.2) |
где V, Z и U — векторы внутренних, выходных и входных фазовых переменных блока.
При большом количестве элементов размерность вектора V и порядок системы уравнений (13.2) становятся чрезмерно большими и требуют упрощения.
При переходе к более высокому иерархическому уровню упрощения они основаны на исключении из модели вектора внутренних переменных V. Полученная модель представляет собой систему уравнений
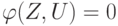 |
( 13.3) |
существенно меньшей размерности, чем полная модель (13.2), и называется макромоделью. Следовательно, макромодель уже не описывает процессы внутри блока, а характеризует только процессы взаимодействия данного блока с другими в составе системы блоков.
Модели (13.2) и (13.3) относятся друг к другу как полная модель и макромодель на п -м уровне иерархии. На более высоком (п–1) -м уровне блок А рассматривается как элемент, и макромодель (13.3) становится моделью элемента А. Следовательно, модели (13.1) и (13.3) относятся друг к другу как модели элементов соседних иерархических уровней. Из моделей типа (13.3) может быть составлена полная модель системы на (п–1) -м уровне.
13.2. Микро-, макро- и метауровни
В зависимости от сложности объекта при его проектировании используют большее или меньшее число уровней абстракции. Объединение уровней, родственных по характеру используемого математического аппарата, приводит к образованию в иерархии функциональных моделей для большинства проектируемых сложных объектов трех укрупненных уровней: микро-, макро- и метауровня.
На микроуровне используют математические модели, описывающие физическое состояние и процессы в сплошных средах. Для моделирования применяют аппарат уравнений математической физики. Примерами таких уравнений служат дифференциальные уравнения в частных производных — уравнения электродинамики, теплопроводности, упругости, газовой динамики. Эти уравнения описывают поля электрического потенциала и температуры в полупроводниковых кристаллах интегральных схем, напряженно-деформированное состояние деталей механических конструкций и т. п.
К типичным фазовым переменным на микроуровне относятся электрические потенциалы, давление, температура, концентрации частиц, плотности токов, механические напряжения и деформации. Независимыми переменными являются время и пространственные координаты. В качестве операторов F и  в уравнениях (13.2) фигурируют дифференциальные и интегральные операторы. Уравнения (13.2), дополненные краевыми условиями, составляют ММ объектов на микроуровне. Анализ таких моделей сводится к решению краевых задач математической физики.
в уравнениях (13.2) фигурируют дифференциальные и интегральные операторы. Уравнения (13.2), дополненные краевыми условиями, составляют ММ объектов на микроуровне. Анализ таких моделей сводится к решению краевых задач математической физики.
На макроуровне производится дискретизация пространств с выделением в качестве элементов отдельных деталей, дискретных электрорадиоэлементов, участков полупроводниковых кристаллов. При этом из числа независимых переменных исключают пространственные координаты. Функциональные модели на макроуровне представляют собой системы алгебраических или обыкновенных дифференциальных уравнений. Для их получения и решения используют соответствующие численные методы. В качестве фазовых переменных фигурируют электрические напряжения, токи, силы, скорости, температуры, расходы и т. д. Они характеризуют проявления внешних свойств элементов при их взаимодействии между собой и внешней средой в электронных схемах или механических конструкциях.
На метауровне с помощью дальнейшего абстрагирования от характера физических процессов удается получить приемлемое по сложности описание информационных процессов, протекающих в проектируемых объектах. На метауровне для моделирования аналоговой РЭС широко применяют аппарат анализа систем автоматического управления, а для моделирования цифровой РЭА — математическую логику, теорию конечных автоматов, теорию массового обслуживания. Математические модели на метауровне — системы обыкновенных дифференциальных уравнений, системы логических уравнений, имитационные модели систем массового обслуживания.
13.2.1. Математические модели на микроуровне
Модели на микроуровне используются для исследования напряженного состояния деталей конструкции и для расчетов их на прочность. Напряженное состояние деталей конструкции в зависимости от геометрии исследуемого узла, вида приложенной нагрузки и свойств материала описывается дифференциальными уравнениями различного вида. Любое из этих уравнений может быть получено из общего квазигармонического уравнения
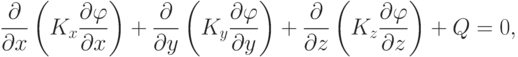 |
( 13.4) |
где х, у, z — пространственные координаты;  — искомая непрерывная функция; Кх, Ку, Kz — коэффициенты; Q — внешнее воздействие.
— искомая непрерывная функция; Кх, Ку, Kz — коэффициенты; Q — внешнее воздействие.
В двумерном случае при Кх = Kv = 1 уравнение (13.4) сводится к уравнению, которое описывает напряженное состояние, возникающее в поперечном сечении упругого однородного стержня под воздействием крутящего момента М:
 |
( 13.5) |
где Е — модуль сдвига материала стержня;  — угол закручивания на единицу длины,
— угол закручивания на единицу длины,  — функция, связанная с напряжениями сдвига
— функция, связанная с напряжениями сдвига 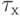 и
и 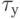 уравнениями
уравнениями
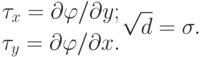 |
( 13.6) |
В уравнение (13.6) в явном виде не входит крутящий момент, связанный с искомой функцией напряжения  уравнением
уравнением
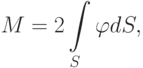 |
( 13.7) |
где S — площадь рассматриваемого сечения.
Точное решение краевых задач получают только в частных случаях. Поэтому реализация таких моделей заключается в использовании различных приближенных моделей. Широкое распространение получили модели на основе интегральных уравнений и модели на основе метода сеток. Одним из наиболее популярных методов решения краевых задач в САПР является метод конечных элементов.
13.2.2. Математические модели на макроуровне
Большинство технических подсистем характеризуется фазовыми переменными. Фазовые переменные образуют вектор неизвестных в ММ технической системы. Для каждой физической подсистемы характерны свои законы, однако для простейших элементов форма выражающих их уравнений оказывается одинаковой. Ниже приводятся в качестве примера электрическая и механическая подсистемы.
Электрическая подсистема
Фазовыми переменными электрической подсистемы являются токи I и напряжения U. Запишем уравнения трех типов простейших элементов.
- Уравнение сопротивления (закон Ома) I = U/R, где R — электрическое сопротивление.
- Уравнение емкости I = C(dU/dt), где С — электрическая емкость.
- Уравнение индуктивности U = L(dI/dt), где L — электрическая индуктивность.
Механическая поступательная система
Фазовые переменные механической поступательной подсистемы — силы F и скорости V — соответственно аналоги токов и напряжений. Запишем уравнения трех типов простейших элементов:
- Уравнение вязкого трения F = V/RM, где RM = 1/k — аналог электрического сопротивления; к — коэффициент вязкого трения.
- Уравнение массы (уравнение второго закона Ньютона) F = mа = См (dV/dt), где а = dV/dt — ускорение; См = m — аналог электрической емкости (масса элемента).
- Уравнение пружины F = kх, где х — перемещение; k — жесткость пружины.
Продифференцируем обе части уравнения по времени: dF/dt = kV, или V = LM(dF/dt), где LM = 1/k — аналог электрической индуктивности.
Аналогичное компонентное уравнение можно получить из закона Гука для элемента, у которого учитывается сжимаемость, т.е. 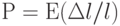 , где Р — напряжение в элементе; Е — модуль Юнга; l — длина элемента; А1 — изменение длины элемента. Умножив обе части этого уравнения на площадь S поперечного сечения элемента и продифференцировав по времени, получим
, где Р — напряжение в элементе; Е — модуль Юнга; l — длина элемента; А1 — изменение длины элемента. Умножив обе части этого уравнения на площадь S поперечного сечения элемента и продифференцировав по времени, получим 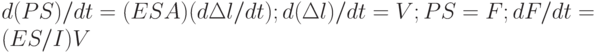 , или V=LM=(dF/dt); LM = 1/(ES).
, или V=LM=(dF/dt); LM = 1/(ES).
Механическая вращательная подсистема
Фазовые переменные этой подсистемы — моменты сил М и угловые скорости  — соответственно, аналоги токов и напряжений. Запишем уравнения трех типов простейших элементов.
— соответственно, аналоги токов и напряжений. Запишем уравнения трех типов простейших элементов.
- Уравнение вязкого трения вращения
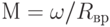 , где Rвр – 1/k — аналог электрического сопротивления; k — коэффициент трения вращения.
, где Rвр – 1/k — аналог электрического сопротивления; k — коэффициент трения вращения. - Основное уравнение динамики вращательного движения
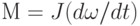 , где J — аналог электрической емкости (момент инерции элемента).
, где J — аналог электрической емкости (момент инерции элемента). - Уравнение кручения бруса с круглым поперечным сечением
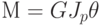 , где М — крутящий момент; G — модуль сдвига; Jp — полярный момент инерции сечения;
, где М — крутящий момент; G — модуль сдвига; Jp — полярный момент инерции сечения; 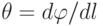 — относительный угол закручивания.
— относительный угол закручивания.
Рассмотрим брус конечной длины, тогда 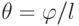 , где
, где  — угол закручивания; l — длина бруса. Продифференцируем обе части уравнения по времени, т. е.
— угол закручивания; l — длина бруса. Продифференцируем обе части уравнения по времени, т. е.  , или если учесть, что
, или если учесть, что 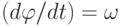 и Lвр = l/(GJp), то
и Lвр = l/(GJp), то 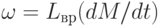 , где Lвр — аналог электрической индуктивности (вращательная гибкость).
, где Lвр — аналог электрической индуктивности (вращательная гибкость).
Аналогичное компонентное уравнение можно получить для спиральной пружины, 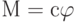 , где с — жесткость пружины. Продифференцировав обе части уравнения по времени, получим
, где с — жесткость пружины. Продифференцировав обе части уравнения по времени, получим 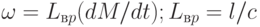 .
.