|
По первому тесту выполнил дважды задания. Результат получается правильный (проверял калькулятором). Пишет, что "Задание не проверено" и предлагает повторить. |
Общие сведения о языке программирования Free Pascal
С подробным описанием приведённых в этой главе функций и множеством других функций можно ознакомиться в справочной системе Lazarus.
Рассмотрим решение задачи с использованием стандартных функций.
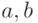 и
и  . Вычислить площадь
. Вычислить площадь  , периметр
, периметр  и величины углов ?, ? и ? треугольника (рис. 2.6).
и величины углов ?, ? и ? треугольника (рис. 2.6).Прежде чем приступить к написанию программы, вспомним математические формулы, необходимые для решения задачи. Для вычисления площади треугольника применим теорему Герона:  , где
, где 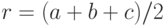 — полупериметр; один из углов найдём по теореме косинусов:
— полупериметр; один из углов найдём по теореме косинусов:
| Компонент | Свойство Caption |
|---|---|
| Form1 | Параметры треугольника |
| Label1 | Введите длины сторон |
| Label2 | a= |
| Label3 | b= |
| Label4 | с= |
| Label5 | Величины углов |
| Label6 | alfa= |
| Label7 | beta= |
| Label8 | gamma= |
| Label9 | Периметр P= |
| Label10 | Площадь S= |
| Button1 | ВЫЧИСЛИТЬ |
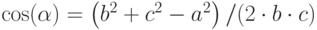 ; второй по теореме синусов:
; второй по теореме синусов: 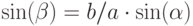 ; третий по формуле:
; третий по формуле: 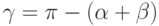 .
.
Решение задачи можно разбить на следующие этапы:
- Определение значений
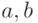 и
и  (ввод величин
(ввод величин 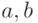 и
и  в память компьютера).
в память компьютера). - Расчёт значений S, P, ?, ? и ? и
 по приведённым выше формулам.
по приведённым выше формулам. - Вывод значений S, P, ?, ? и ? и
 .
.
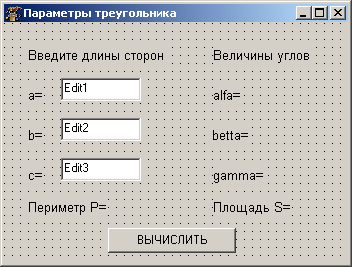
Процесс разработки несложного программного интерфейса описан в главе 1. Попытайтесь самостоятельно разработать внешний вид данной программы. Разместите на форме десять меток, три поля ввода и одну кнопку. Измените заголовки формы и меток (свойство Caption) в соответствии с табл. 2.11. В качестве свойства Text компонентов Edit1, Edit2, Edit3 установите пробел. В результате форма должна выглядеть так, как показано на рис. 2.7.
Итак, проект формы готов. В окне программного кода среды Lazarus автоматически сформировал структуру модуля, перечислив названия основных разделов. Двойной щелчок по кнопке Вычислить приведёт к созданию процедуры TForm1.Button1Click в разделе implementation:
procedure TForm1. Button1Click ( Sender : TObject ); begin end;
и её описанию в разделе interface. Понятно, что созданная процедура не содержит ни одной команды. Задача программиста — заполнить шаблон описаниями и операторами. Все команды, указанные в процедуре между словами begin и end, будут выполнены при щелчке по кнопке Выполнить. В нашем случае процедура TForm1.Button1Click будет иметь вид:
procedure TForm1. Button1Click ( Sender : TObject ); //Описание переменных: // a, b, с - стороны треугольника; // alfa, beta, gamma - углы треугольника; // S - площадь треугольника; // r - полупериметр треугольника //Все переменные вещественного типа. var a, b, c, alfa, beta, gamma, S, r : real; begin //Из полей ввода Edit1, Edit2, Edit3 считываются введенные строки, //с помощью функции StrToFloat(х) преобразовываются //в вещественные числа и записываются в переменные а, b, c. a:= StrToFloat ( Edit1. Text ); b:= StrToFloat ( Edit2. Text ); c := StrToFloat ( Edit3. Text ); //Вычисление значения полупериметра. r :=( a+b+c ) / 2; //Вычисление значения площади, //для вычисления применяется функция: // sqrt(х) - корень квадратный из х. S:= sqrt ( r * ( r - a ) * ( r - b ) * ( r - c ) ); //Вычисление значения угла alfa в радианах. //Для вычисления применяем функции: // acos(х) - арккосинус x; // sqr(х) - возведение х в квадрат. alfa := arccos ( ( sqr ( b)+ sqr ( c)-sqr ( a ) ) / 2 / b/ c ); //Вычисление значения угла beta в радианах. //Для вычисления применяем функции: // asin(х) - арксинус x; beta := arcsin ( b/a * sin ( a l f a ) ); //Вычисление значения угла gamma в радианах. //Математическая постоянная определена функцией без аргумента pi. gamma:= pi -( alfa+beta ); //Перевод из радиан в градусы. alfa := alfa * 180/ p i; beta := beta * 180/ p i; gamma:=gamma * 180/ p i; //Для вывода результатов вычислений используем //операцию слияния строк "+" и функцию FloatToStrF(х), //которая преобразовывает вещественную переменную х в строку //и выводит ее в указанном формате, в нашем случае //под переменную отводится три позиции, включая точку //и ноль позиций после точки. //Величины углов в градусах выводятся на форму //в соответствующие объекты типа надпись. Label6. Caption := ’ alfa= ’+FloatToStrF ( alfa, ffFixed, 3, 0 ); Label7. Caption := ’ beta= ’+FloatToStrF ( beta, ffFixed, 3, 0 ); Label8. Caption := ’gamma= ’+FloatToStrF (gamma, ffFixed, 3, 0 ); //Используем функцию FloatToStrF(х) для форматированного //вывода, в нашем случае под все число отводится пять позиции, //включая точку, и две позиций после точки. //Значения площади и периметра выводятся на форму. Label9. Caption := ’Периметр P= ’+FloatToStrF (2 * r, ffFixed, 5, 2 ); Label10. Caption := ’Площадь S= ’+FloatToStrF ( S, ffFixed, 5, 2 ); end;
Обратите внимание, что были написаны всего десять команд, предназначенных для решения поставленной задачи. Остальной текст в окне редактора создаётся автоматически. В результате весь программный код (без комментариев) имеет вид:
unit Unit1;
{$mode objfpc}{$H+}
interface
uses
Classes, SysUtils, LResources, Forms, Controls, Graphics,
Dialogs, StdCtrls, Math;
type
{ TForm1 }
TForm1 = class (TForm)
Button1 : TButton;
Edit1 : TEdit;
Edit2 : TEdit;
Edit3 : TEdit;
Label1 : TLabel;
Label10 : TLabel;
Label2 : TLabel;
Label3 : TLabel;
Label4 : TLabel;
Label5 : TLabel;
Label6 : TLabel;
Label7 : TLabel;
Label8 : TLabel;
Label9 : TLabel;
procedure Button1Click ( Sender : TObject );
private
{ private declarations }
public
{ public declarations }
end;
var
Form1 : TForm1;
implementation
{ TForm1 }
procedure TForm1. Button1Click ( Sender : TObject );
var a, b, c, alfa, beta, gamma, S, r : real;
begin
a:= StrToFloat ( Edit1. Text );
b:= StrToFloat ( Edit2. Text );
c := StrToFloat ( Edit3. Text );
r :=( a+b+c ) / 2;
S:= sqrt ( r * ( r - a ) * ( r - b ) * ( r - c ) );
alfa := arccos ( ( sqr ( b)+ sqr ( c)-sqr ( a ) ) / 2 / b/ c );
beta := arcsin ( b/a * sin ( alfa ) );
gamma:= pi -( alfa+beta );
alfa := alfa * 180/ p i;
beta := beta * 180/ p i;
gamma:=gamma * 180/ p i;
Label6. Caption := ’ a l f a= ’+FloatToStrF ( alfa, ffFixed, 3, 0 );
Label7. Caption := ’ beta= ’+FloatToStrF ( beta, ffFixed, 3, 0 );
Label8. Caption := ’gamma= ’+FloatToStrF (gamma, ffFixed, 3, 0 );
Label9. Caption := ’Периметр P= ’+
FloatToStrF (2 * r, ffFixed, 5, 2 );
Label10. Caption := ’Площадь S= ’+FloatToStrF ( S, ffFixed, 5, 2 );
end;
initialization
{$I unit1.lrs}
end.
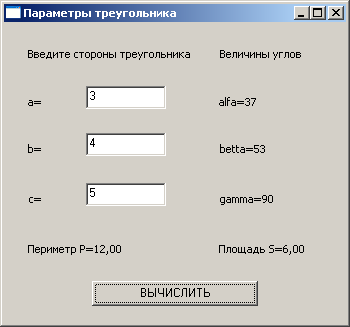
На рис. 2.8 представлено диалоговое окно, которое появится, если запустить эту программу, щёлкнув по кнопке Вычислить.
Теперь напишем консольное приложение для решения этой задачи. Для этого запустим текстовый редактор Geany. Выполним команду Файл — New with Template — Pascal Source File. В открывшемся окне реактора введём следующий текст программы.
program pr3; //Подключение модуля для работы с математическими функциями, //см. табл. 2.6. uses math; //Описание всех используемых переменных. var a, b, c, r, s, alfa, beta, gamma : real; begin //Ввод сторон трегольника. writeln ( ’Введите стороны треугольника ’ ); readln ( a, b, c ); //Вычисление значения полупериметра. R:=( a+b+c ) / 2; //Вычисление значения площади, //для вычисления применяется функция: // sqrt(х) — корень квадратный из х. S:= sqrt ( r * ( r - a ) * ( r - b ) * ( r - c ) ); //Вычисление значения угла alfa в радианах. //Для вычисления применяем функции: // acos(х) - арккосинус x; // sqr(х) — возведение х в квадрат. alfa := arccos ( ( sqr ( b)+ sqr ( c) - sqr ( a ) ) / 2 / b/ c ); //Вычисление значения угла beta в радианах. //Для вычисления применяем функции: // asin(х) - арксинус x; beta := arcsin ( b/a * sin ( alfa ) ); //Вычисление значения угла gamma в радианах. //Математическая постоянная определена //функцией без аргумента pi. gamma:= pi - ( alfa+beta ); //Перевод из радиан в градусы. alfa := alfa * 180/ p i; beta := beta * 180/ p i; gamma:=gamma * 180/ p i; //Вывод площади и сторон треугольника. writeln ( ’Площадь треугольника = ’, S : 6 : 2 ); writeln ( ’ alf= ’, alfa : 6 : 2, ’ bet= ’, beta : 6 : 2, ’ gam= ’,gamma : 6 : 2 ); end.
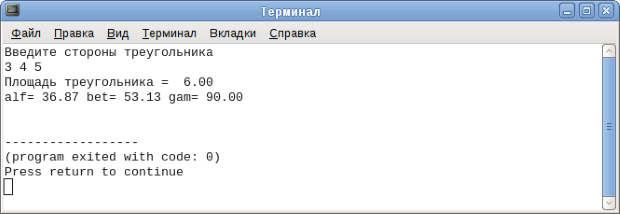
Для компиляции программы в Geany необходимо выполнить команду Построить — Собрать (F8), для запуска — Построить — Выполнить (F5). На рис. 2.9 представлены результаты работы программы.
Введите стороны треугольника 3 4 5 Площадь треугольника = 6.00 alf= 36.87 bet= 53.13 gam= 90.00