НОУ ИНТУИТ | Программирование на языке С++ в среде Qt Creator. Лекция 9: Структуры в языке C++

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 07.03.2015 | Уровень: для всех | Доступ: платный | ВУЗ: Компания ALT Linux

|

Вам нравится? Нравится 77 студентам

| Поделиться |

Поддержать программу

Задача 9.4. Написать программу умножения матриц комплексных чисел. Матрицы и имеют вид:

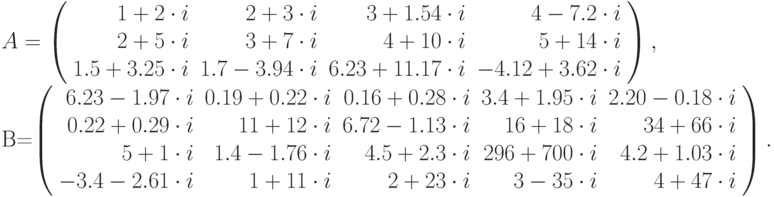
$A=\left(\begin{array}{rrrr}1+2\cdot i&2+3\cdot i&3+1.54\cdot i&4-7.2\cdot i\\2+5\cdot i&3+7\cdot i&4+10\cdot i&5+14\cdot i\\1.5+3.25\cdot i&1.7-3.94\cdot i&6.23+11.17\cdot i&-4.12+3.62\cdot i\end{array}\right), \noindent B=\left(\begin{array}{rrrrr}6.23-1.97\cdot i&0.19+0.22\cdot i&0.16+0.28\cdot i&3.4+1.95\cdot i&2.20-0.18\cdot i\\0.22+0.29\cdot i&11+12\cdot i&6.72-1.13\cdot i&16+18\cdot i&34+66\cdot i\\5+1\cdot i&1.4-1.76\cdot i&4.5+2.3\cdot i&296+700\cdot i&4.2+1.03\cdot i\\-3.4-2.61\cdot i&1+11\cdot i&2+23\cdot i&3-35\cdot i&4+47\cdot i\end{array}\right).$

Пусть исходные данные хранятся в файле abc.txt. Данные к задаче 9.4, содержимое файла abc.txt:

3 4 5
(1,2) (2,3) (3,1.54) (4,-7.2)
(2,5) (3,7) (4,10) (5,14)
(1.5,3.25) (1.7,-3.94) (6.23,11.17) (-4.12,3.62)

(6.23,-1.97) (0.19,0.22) (0.16,0.28) (3.4,1.95) (2.20,-0.18)
(0.22,0.29) (11,12) (6.72,-1.13) (16,18) (34,66)
(5,1) (1.4,-1.76) (4.5,2.3) (296,700) (4.2,1.03)
(-3.14,-2.61) (1,11) (2,23) (3,-35) (4,47)

Далее приведён текст программы, реализующий алгоритм решения задачи 9.4.

#include <iostream>
#include <fstream>
#include <math.h>
#include <complex>
using namespace std;
int main ( )
{
int i, j, p,N,M,K;
complex <float > **A, **B, **C;
ifstream f;
ofstream g;
f.open ( " abc.txt " );
f>>N>>M>>K;
cout<<" N = "<<N<<" \tM = "<<M<<" \tK = "<<K<<endl;
A=new complex <float > * [N ];
for ( i =0; i<N;A [ i ]=new complex <float > [M], i++);
B=new complex <float > * [M];
for ( i =0; i<M;B [ i ]=new complex <float > [K ], i++);
C=new complex <float > * [N ];
for ( i =0; i<N;C [ i ]=new complex <float > [K ], i++);
for ( i =0; i<N; i++)
	for ( j =0; j<M; f>>A [ i ] [ j ], j++);
cout<<"Матрица A\n ";
for ( i =0; i<N; cout<<endl, i++)
	for ( j =0; j<M; cout<<A [ i ] [ j ]<<" \t ", j++);
for ( i =0; i<M; i++)
	for ( j =0; j<K; f>>B [ i ] [ j ], j++);
cout<<"Матрица B\n ";
for ( i =0; i<M; cout<<endl, i++)
	for ( j =0; j<K; cout<<B [ i ] [ j ]<<" \t ", j++);
for ( i =0; i<N; i++)
	for ( j =0; j<K; j++)
		for (C [ i ] [ j ]=p=0;p<M; p++)
			C [ i ] [ j ]+=A [ i ] [ p ] *B [ p ] [ j ];
f.close ( );
cout<<"Матрица C\n ";
for ( i =0; i<N; cout<<endl, i++)
	for ( j =0; j<K; cout<<C [ i ] [ j ]<<" \t ", j++);
g.open ( " result.t x t " );
g<<"Матрица C=A*B\n ";
for ( i =0; i<N; g<<endl, i++)
	for ( j =0; j<K; g<<C [ i ] [ j ]<<" \t ", j++);
g.close ( );
return 0;
}

Результат умножения матриц из задачи 9.4 (файл result.txt):

Матрица C=A*B
(-8.152,34.598)		(75.8604,91.276)	(199.988,109.93)	(-452.5,2486.99)	(237.974,406.978)
(51.78,26.61)		(-177.52,190.35)	(-290.01,242.21)	(-5391.95,5813.9)	(-986.2,783.76)
(59.6291,78.3851)	(49.9912,-59.0193)	(-82.8542,-50.3838)	(-5763.7,7803.92)	(149.766,-140.709)

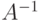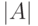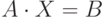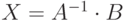Задача 9.5. Заданы матрицы и . Необходимо вычислить матрицу $A^{-1}$ , обратную к матрице , найти определитель |A| матрицы и решить матричное уравнение $A\cdot X=B$ , где $X=A^{-1}\cdot B$ . Матрицы и имеют вид:

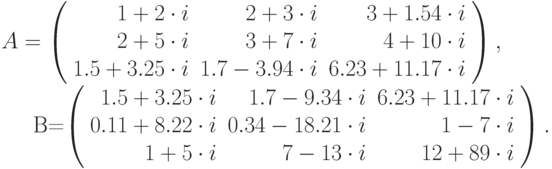
$A=\left(\begin{array}{rrr}1+2\cdot i&2+3\cdot i&3+1.54\cdot i\\2+5\cdot i&3+7\cdot i&4+10\cdot i\\1.5+3.25\cdot i&1.7-3.94\cdot i&6.23+11.17\cdot i\end{array}\right), B=\left(\begin{array}{rrr}1.5+3.25\cdot i&1.7-9.34\cdot i&6.23+11.17\cdot i\\0.11+8.22\cdot i&0.34-18.21\cdot i&1-7\cdot i\\1+5\cdot i&7-13\cdot i&12+89\cdot i\end{array}\right).$

Для хранения исходных данных создадим текстовый файл abc2.txt следующего содержания:

3
(1,2) (2,3) (3,1.54)
(2,5) (3,7) (4,10)
(1.5,3.25) (1.7,-9.34) (6.23,11.17)

(1.5,3.25) (1.7,-9.34) (6.23,11.17)
(0.11,8.22) (0.34,-18.21) (1,-7)
(1,5) (7,-13) (12,89)

Текст программы, реализующий поставленную задачу, представлен ниже.

#include <iostream>
#include <fstream>
#include <math.h>
#include <complex>
using namespace std;
//Решение СЛАУ с комплексными коэффициентами
int SLAU( complex <float > ** matrica_a, int n, complex <float > *massiv_b,
complex <float > *x )
{
int i, j, k, r;
complex <float > c,M, s;
float max;
complex <float > **a, *b;
a=new complex <float > *[ n ];
for ( i =0; i<n; i++)
	a [ i ]=new complex <float >[n ];
b=new complex <float > [ n ];
for ( i =0; i<n; i++)
	for ( j =0; j<n; j++)
		a [ i ] [ j ]=matrica_a [ i ] [ j ];
for ( i =0; i<n; i++)
	b [ i ]=massiv_b [ i ];
for ( k=0;k<n; k++)
{
	max= abs ( a [ k ] [ k ] );
	r=k;
	for ( i=k+1; i<n; i++)
		if ( abs ( a [ i ] [ k ] )>max)
		{
			max=abs ( a [ i ] [ k ] );
			r= i;
		}
	for ( j =0; j<n; j++)
	{
		c=a [ k ] [ j ];
		a [ k ] [ j ]=a [ r ] [ j ];
		a [ r ] [ j ]= c;
	}
	c=b [ k ];
	b [ k ]=b [ r ];
	b [ r ]= c;
	for ( i=k+1; i<n; i++)
	{
		for (M=a [ i ] [ k ] / a [ k ] [ k ], j=k; j<n; j++)
			a [ i ] [ j ]_=M_a [ k ] [ j ];
		b [ i ]-=M*b [ k ];
	}
}
if ( abs ( a [ n -1 ] [ n-1 ])==0)
	if ( abs ( b [ n-1 ])==0)
		return -1;
	else return -2;
else
{
	for ( i=n-1; i >=0; i --)
	{
		for ( s =0, j= i +1; j<n; j++)
			s+=a [ i ] [ j ] * x [ j ];
		x [ i ]=( b [ i ]- s ) /a [ i ] [ i ];
	}
return 0;
}
for ( i =0; i<n; i++)
	delete [ ] a [ i ];
delete [ ] a;
delete [ ] b;
}
//Вычисление обратной матрицы с комплексными коэффициентами
int INVERSE( complex <float > **a, int n, complex <float > **y )
{
int i, j, res;
complex <float > *b, *x;
b=new complex <float > [ n ];
x=new complex <float > [ n ];
for ( i =0; i<n; i++)
{
	for ( j =0; j<n; j++)
		if ( j==i )
		b [ j ]= 1;
		else b [ j ]= 0;
			res=SLAU( a, n, b, x );
	if ( res !=0)
		break;
	else
		for ( j =0; j<n; j++)
			y [ j ] [ i ]=x [ j ];
}
delete [ ] x;
delete [ ] b;
if ( res !=0)
	return -1;
else
	return 0;
}
//Вычисление определителя матрицы с комплексными коэффициентами
complex <float > determinant ( complex <float > ** matrica_a, int n )
{
int i, j, k, r;
complex <float > c,M, s, det =1;
complex <float > **a;
float max;
a=new complex <float > * [ n ];
for ( i =0; i<n; i++)
	a [ i ]=new complex <float >[n ];
for ( i =0; i<n; i++)
	for ( j =0; j<n; j++)
		a [ i ] [ j ]=matrica_a [ i ] [ j ];
for ( k=0;k<n; k++)
{
	max=abs ( a [ k ] [ k ] );
	r=k;
	for ( i=k+1; i<n; i++)
		if ( abs ( a [ i ] [ k ] )>max)
		{
			max=abs ( a [ i ] [ k ] );
			r= i;
		}
	if ( r !=k ) det=-det;
		for ( j =0; j<n; j++)
		{
			c=a [ k ] [ j ];
			a [ k ] [ j ]=a [ r ] [ j ];
			a [ r ] [ j ]= c;
		}
	for ( i=k+1; i<n; i++)
		for (M=a [ i ] [ k ] / a [ k ] [ k ], j=k; j<n; j++)
			a [ i ] [ j ]-=M*a [ k ] [ j ];
}
for ( i =0; i<n; i++)
	det*=a [ i ] [ i ];
return det;
for ( i =0; i<n; i++)
	delete [ ] a [ i ];
delete [ ] a;
}
//Умножение матриц с комплексными коэффициентами
void umn ( complex <float > **a, complex <float > **b, complex <float > **c, int
	n, int m, int k )
{
int i, j, p;
for ( i =0; i<n; i++)
	for ( j =0; j<k; j++)
		for ( c [ i ] [ j ]=p=0;p<m; p++)
			c [ i ] [ j ]+=a [ i ] [ p ] * b [ p ] [ j ];
}
int main ( )
{
int i, j,N;
complex <float > **A, **B, **X, **Y;
ifstream f;
ofstream g;
f.open ( " abc2.txt " );
f>>N;
cout<<" N = "<<N<<endl;
A=new complex <float > * [N ];
for ( i =0; i<N; i++)
	A [ i ]=new complex <float > [N ];
B=new complex <float > * [N ];
for ( i =0; i<N; i++)
	B [ i ]=new complex <float > [N ];
X=new complex <float > * [N ];
for ( i =0; i<N; i++)
	X [ i ]=new complex <float > [N ];
Y=new complex <float > * [N ];
for ( i =0; i<N; i++)
	Y [ i ]=new complex <float > [N ];
for ( i =0; i<N; i++)
	for ( j =0; j<N; j++)
		f>>A [ i ] [ j ];
cout<<"Матрица A\n ";
for ( i =0; i<N; cout<<endl, i++)
	for ( j =0; j<N; j++)
		cout<<A [ i ] [ j ]<<" \t ";
for ( i =0; i<N; i++)
	for ( j =0; j<N; j++)
		f>>B [ i ] [ j ];
cout<<"Матрица B\n ";
for ( i =0; i<N; cout<<endl, i++)
	for ( j =0; j<N; j++)
		cout<<B [ i ] [ j ]<<" \t ";
if ( ! INVERSE(A, N, X) )
{
	cout<<"Обратная матрица\n ";
	for ( i =0; i<N; cout<<endl, i++)
		for ( j =0; j<N; j++)
			cout<<X [ i ] [ j ]<<" \t ";
	umn(X, B,Y,N,N,N);
	cout<<" \n Решение матричного уравнения \n ";
	for ( i =0; i<N; cout<<endl, i++)
		for ( j =0; j<N; j++)
			cout<<Y [ i ] [ j ]<<" \t ";
}
else cout<<"Не существует обратной матрицы\n ";
cout<<"Определитель= "<<determinant (A,N);
return 0;
}

Результат работы программы к задаче 9.5:

N=3
Матрица A
(1,2) (2,3) (3,1.54)
(2,5) (3,7) (4,10)
(1.5,3.25) (1.7,-9.34) (6.23,11.17)
Матрица B
(1.5,3.25) (1.7,-9.34) (6.23,11.17)
(0.11,8.22) (0.34,-18.21) (1,-7)
(1,5) (7,-13) (12,89)
Обратная матрица
(-0.495047,-0.748993) (0.325573,0.182901) (-0.0340879,-0.0958618)
(0.125154,0.0765918) (-0.058179,-0.0728342) (0.00208664,0.0685887)
(0.157733,0.322512) (-0.0859214,-0.127174) (0.0143863,-0.000518244)
Определитель=(7.50219,-208.261)
Решение матричного уравнения
(0.669246,-0.302366) (-5.88068,-2.74393) (15.0106,-16.4762)
(0.190248,0.114415) (0.488295,0.448942) (-6.72319,3.21833)
(0.241332,0.347549) (1.02932,0.405788) (-3.37716,5.51956)

Дальше >>

Программирование на языке С++ в среде Qt Creator

Программирование на языке С++ в среде Qt Creator

Структуры в языке C++

Вопросы и ответы

Студенты

Авторизоваться

Программирование на языке С++ в среде Qt Creator

Программирование на языке С++ в среде Qt Creator

Структуры в языке C++

Вопросы и ответы

Студенты