НОУ ИНТУИТ | Программирование на языке С++ в среде Qt Creator. Лекция 9: Структуры в языке C++

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 07.03.2015 | Уровень: для всех | Доступ: платный | ВУЗ: Компания ALT Linux

|

Вам нравится? Нравится 77 студентам

| Поделиться |

Поддержать программу

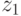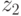Задача 9.2. Даны два комплексных числа z_1 и z_2 . Выполнить над ними основные операции:

сложение ,
вычитание ,
умножение $z_1\cdot z_2$ ,
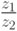деление $\frac{z_1}{z_2}$ ,
возведение в степень $n\ z_1^n$ ,
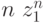извлечение корня -й степени $\sqrt[n]{z_1}$
вычисление комплексного сопряжённого числа $\bar{z}_1$ .

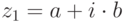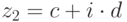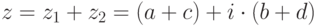Суммой двух комплексных чисел $z_1=a+i\cdot b$ и $z_2=c+i\cdot d$ называется комплексное число $z=z_1+z_2=(a+c)+i\cdot (b+d)$ .

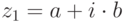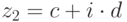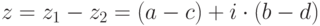Разностью двух комплексных чисел $z_1=a+i\cdot b$ и $z_2=c+i\cdot d$ называется комплексное число $z=z_1-z_2=(a-c)+i\cdot (b-d)$ .

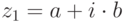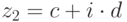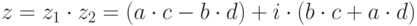Произведением двух комплексных чисел $z_1=a+i\cdot b$ и $z_2=c+i\cdot d$ называется комплексное число $z=z_1\cdot {z_2}=(a\cdot c-b\cdot d)+i\cdot (b\cdot c+a\cdot d)$ .

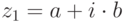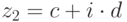Частным двух комплексных чисел $z_1=a+i\cdot b$ и $z_2=c+i\cdot d$ называется комплексное число

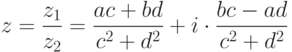
$z=\frac{z_1}{z_2}=\frac{ac+bd}{c^2+d^2}+i\cdot {\frac{bc-ad}{c^2+d^2}}$

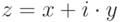Числом, сопряжённым комплексному числу $z=x+i\cdot y$ , называется число 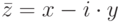$\bar{z}=x-i\cdot y$ (рис. 9.2).

Всякое комплексное число, записанное в алгебраической форме 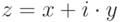$z=x+i\cdot y$ , можно записать в тригонометрической 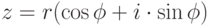$z=r(\cos \phi+i\cdot \sin \phi)$ или в показательной форме 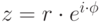$z=r\cdot e^{i\cdot \phi}$ , где $r=\sqrt{x^2+y^2}$ — модуль комплексного числа $z,\ \phi=\arctan \frac{y}{x}$ — его аргумент (рис. 9.2).

Для возведения в степень комплексного числа, записанного в тригонометрической форме 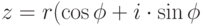$z=r(\cos\phi+i\cdot \sin \phi$ ), можно воспользоваться формулой Муавра

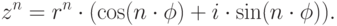
$z^n=r^n\cdot (\cos (n\cdot \phi)+i\cdot \sin (n\cdot \phi)).$

Формула для извлечения корня

-й степени из комплексного числа $z=r\cdot (\cos \phi+i\cdot \sin \phi)$ имеет вид

$\sqrt[n]z=\sqrt[n]z(\cos \frac{\phi+2\cdot \pi \cdot k}{n}+i\cdot \sin \frac{\phi+2\cdot \pi \cdot k}{n}),$

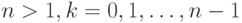где $n>1,k=0,1,\dots,n-1$ .

Далее приведён текст программы, реализующий алгоритм решения задачи 9.2. В программе описаны две структуры для работы с комплексными числами: структура complex1 для представления комплексных чисел в алгебраической форме (Re — действительная часть комплексного числа, Im — его мнимая часть) и структура complex2 для представления комплексных чисел в показательной или тригонометрической форме (Modul — модуль комплексного числа, Argum — его аргумент). Кроме того в программе созданы функции, реализующие основные действия над комплексными числами, переход между различными формами представления комплексных чисел, а также ввод-вывод комплексных чисел.

#include <iostream>
#include <math.h>
using namespace std;
struct complex1
{
	float Re;
	float Im;
};
struct complex2
{
	float Modul;
	float Argum;
};
//Ввод числа в алгебраической форме
complex1 vvod1 ( )
{
	complex1 temp;
	cout<<"Введите действительную часть числа\n ";
	cin>>temp.Re;
	cout<<"Введите мнимую часть комплексного числа\n ";
	cin>>temp.Im;
	return temp;
}
//Ввод числа в тригонометрической или показательной форме
complex2 vvod2 ( )
{
	complex2 temp;
	cout<<"Введите модуль комплексного числа\n ";
	cin>>temp.Modul;
	cout<<"Введите аргумент комплексного числа\n ";
	cin>>temp.Argum;
	return temp;
}
//Вывод числа в алгебраической форме
void vivod ( complex1 chislo )
{
	cout<<chislo.Re;
	if ( chislo.Im>=0)
		cout<<" + "<< chislo.Im<<" i "<<endl;
	else
		cout<<" "<< chislo.Im<<" i "<<endl;
}
//Вывод числа в тригонометрической форме
void vivod ( complex2 chislo )
{
	cout<<chislo.Modul<<" ( cos ( "<< chislo.Argum<<" ) + i sin ( "<< chislo.Argum<<
	" ) ) "<<endl;
}
//Перевод числа из тригонометрической формы в алгебраическую,
//pr определяет, выводить или нет полученное число на экран.
complex1 perevod ( complex2 chislo, bool pr=false )
{
	complex1 temp;
	temp.Re=chislo.Modul*cos ( chislo.Argum );
	temp.Im=chislo.Modul*sin ( chislo.Argum );
	if ( pr ) vivod ( temp );
	return temp;
}
//Перевод числа из алгебраической формы в тригонометрическую,
//pr определяет, выводить или нет полученное число на экран.
complex2 perevod ( complex1 chislo, bool pr=false )
{
	complex2 temp;
	temp.Modul=sqrt ( chislo.Re* chislo.Re+
	chislo.Im*chislo.Im );
	temp.Argum=atan ( chislo.Im/ chislo.Re );
	if ( pr ) vivod ( temp );
	return temp;
}
//Функция сложения двух чисел в алгебраической форме,
//pr определяет, выводить или нет число на экран.
complex1 plus1 ( complex1 chislo1, complex1 chislo2, bool pr=true )
{
	complex1 temp;
	temp.Re=chislo1.Re+chislo2.Re;
	temp.Im=chislo1.Im+chislo2.Im;
	if ( pr ) vivod ( temp );
	return temp;
}
//Функция вычитания двух чисел в алгебраической форме,
//pr определяет, выводить или нет число на экран.
complex1 minus1 ( complex1 chislo1, complex1 chislo2, bool pr=true )
{
	complex1 temp;
	temp.Re=chislo1.Re-chislo2.Re;
	temp.Im=chislo1.Im-chislo2.Im;
	if ( pr ) vivod ( temp );
	return temp;
}
//Функция умножения двух чисел в алгебраической форме,
//pr определяет, выводить или нет число на экран.
complex1 mult1 ( complex1 chislo1, complex1 chislo2, bool pr=true )
{
	complex1 temp;
	temp.Re=chislo1.Re* chislo2.Re-chislo1.Im* chislo2.Im;
	temp.Im=chislo1.Im* chislo2.Re+chislo1.Re* chislo2.Im;
	if ( pr ) vivod ( temp );
	return temp;
}
//Функция деления двух чисел в алгебраической форме,
//pr определяет, выводить или нет число на экран.
complex1 divide1 ( complex1 chislo1, complex1 chislo2, bool pr=true )
{
	complex1 temp;
	temp.Re=( chislo1.Re* chislo2.Re+chislo1.Im* chislo2.Im ) / ( chislo2.Re* chislo2 .
	Re+chislo2.Im* chislo2.Im );
	temp.Im=( chislo1.Im* chislo2.Re-chislo1.Re* chislo2.Im ) / ( chislo2.Re* chislo2 .
	Re+chislo2.Im* chislo2.Im );
	if ( pr ) vivod ( temp );
	return temp;
}
//Функция возведения комплексного числа в алгебраической форме
//в целую степень n, pr определяет, выводить или нет полученное число на экран.
complex1 pow1 ( complex1 chislo1, int n, bool pr=true )
{
	complex1 temp;
	complex2 temp2;
	float p=1;
	int i =1;
	temp2=perevod ( chislo1, true ); //Перевод числа в тригонометрическую форму.
	for (; i<=n; p*=temp2.Modul, i++);
	temp.Re=p*cos ( n*temp2.Argum );
	temp.Im=p*sin ( n*temp2.Argum );
	if ( pr ) vivod ( temp );
	return temp;
}
//Функция извлечения корня степени n из комплексного числа
//в алгебраической форме, pr определяет, выводить или нет
//полученные значения на экран. Функция возвращает ro и fi.
void sqrt n 1 ( complex1 chislo1, int n, float _ ro, float _ f i, bool pr=true )
{
	complex1 temp;
	complex2 temp2;
	int i =0;
	temp2=perevod ( chislo1, true ); //Перевод числа в тригонометрическую форму.
	* r o=pow ( temp2.Modul, ( float ) 1/n );
	* f i=temp2.Argum;
	if ( pr )
	{
		for ( i =0; i<n; i++)
		{
			cout<<i<<"-е значение корня\n ";
			temp.Re=*ro* cos ( ( * fi +2*M_PI* i ) /n );
			temp.Im=*ro* sin ( ( * fi +2*M_PI* i ) /n );
			vivod ( temp );
		}
	}
}
int main ( )
{
	complex1 chislo1, chislo2; //Описание комплексных
	complex1 chislo5; //чисел в алгебраической форме.
	complex2 chislo3, chislo4; //Описание комплексных чисел в тригонометрической форме.
	float ro1, fi1;
	chislo1=vvod1 ( ); //Ввод исходных данных
	chislo2=vvod1 ( ); //в алгебраической форме.
	vivod ( chislo1 ); //Вывод исходных данных
	vivod ( chislo2 ); //в алгебраической форме.
	chislo 3=perevod ( chislo1, true ); //Перевод чисел
	chislo 4=perevod ( chislo2, true ); //в тригонометрическую форму и вывод их на экран.
	cout<<"Сумма чисел ";
	chislo5=plus1 ( chislo1, chislo2, true );
	cout<<"Разность чисел ";
	chislo5=minus1 ( chislo1, chislo2, true );
	cout<<"Произведение чисел ";
	chislo5=mult1 ( chislo1, chislo2, true );
	cout<<"Частное чисел ";
	chislo5=divide1 ( chislo1, chislo2, true );
	chislo5=pow1 ( chislo1, 5, true ); //Возведение числа в пятую степень.
	sqrtn1 ( chislo1, 5, &Ro1, &fi1, true ); //Извлечение корня пятой степени.
	return 0;
}

Результаты работы программы к задаче 9.2.

Введите действительную часть числа
5
Введите мнимую часть комплексного числа
-7
Введите действительную часть числа
11
Введите мнимую часть комплексного числа
1.85
5 -7 i
11 +1.85 i
8.60233 ( cos (-0.950547) + i sin (-0.950547))
11.1545 ( cos (0.166623) + i sin (0.166623))
Сумма чисел 16 -5.15 i
Разность чисел -6 -8.85 i
Произведение чисел 67.95 -67.75 i
Частное чисел 0.337961 -0.693203 i
8.60233 ( cos (-0.950547) + i sin (-0.950547))
1900 +47068 i
8.60233 ( cos (-0.950547) + i sin (-0.950547))
0-е значение корня
1.51018 -0.290608 i
1-е значение корня
0.743054 +1.34646 i
2-е значение корня
-1.05094 +1.12277 i
3-е значение корня
-1.39257 -0.652552 i
4-е значение корня
0.190285 -1.52606 i

Дальше >>

Программирование на языке С++ в среде Qt Creator

Программирование на языке С++ в среде Qt Creator

Структуры в языке C++

Вопросы и ответы

Студенты

Авторизоваться

Программирование на языке С++ в среде Qt Creator

Программирование на языке С++ в среде Qt Creator

Структуры в языке C++

Вопросы и ответы

Студенты