|
С помощью обобщенного алгоритма Евклида найдите числа х и у, удовлетворяющие уравнению 30х +12y = НОД(30,12). х=1, у=-2, НОД = 6. Где ошибка? |
Поточные шифры и генераторы псевдослучайных чисел. Часть 2
Цель лекции: продолжить знакомство с генераторами псевдослучайных чисел, используемых для поточного шифрования информации, а также с некоторыми режимами блочных шифров для получения псевдослучайных чисел.
Генераторы псевдослучайных чисел на основе сдвиговых регистров с обратной связью
В теории кодирования и криптографии широко применяются так называемые сдвиговые регистры с обратной связью. Они использовались в аппаратуре шифрования еще до начала массового использования ЭВМ и современных высокоскоростных программных шифраторов.
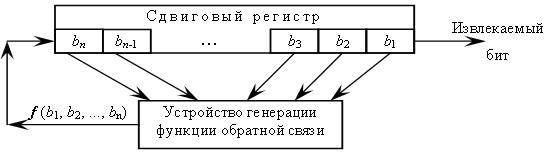
Сдвиговые регистры с обратной связью могут применяться для получения потока псевдослучайных бит. Сдвиговый регистр с обратной связью состоит из двух частей: собственно n-битного сдвигового регистра и устройства обратной связи ( рис. 8.1).
Извлекать биты из сдвигового регистра можно только по одному. Если необходимо извлечь следующий бит, все биты регистра сдвигаются вправо на 1 разряд. При этом на вход регистра слева поступает новый бит, который формируется устройством обратной связи и зависит от всех остальных битов сдвигового регистра. За счет этого биты регистра изменяются по определенному закону, который и определяет схему получения ПСЧ. Понятно, что через некоторое количество тактов работы регистра последовательность битов начнет повторяться. Длина получаемой последовательности до начала ее повторения называется периодом сдвигового регистра.
Поточные шифры с использованием сдвиговых регистров достаточно долго использовались на практике. Это связано с тем, что они очень хорошо реализуются с помощью цифровой аппаратуры.
Простейшим видом сдвигового регистра с обратной связью является линейный сдвиговый регистр с обратной связью (linear feedback shift register – LFSR). Обратная связь в этом устройстве реализуется просто как сумма по модулю 2 всех (или некоторых) битов регистра. Биты, которые участвуют в обратной связи, образуют отводную последовательность. Линейные сдвиговые регистры с обратной связью или их модификации часто применяется в криптографии.
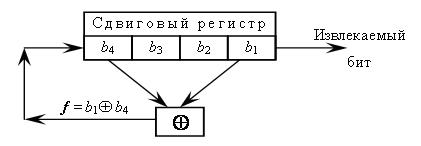
Для того, чтобы стало понятнее, как работает сдвиговый регистр с обратной связью, рассмотрим 4-битовый LFSR с отводом от первого и четвертого разрядов, представленный на рис. 8.2.
Запишем в изображенный на рисунке регистр начальное значение 1011. Вычислять последовательность внутренних состояний регистра удобно с помощью таблицы, представленной на таблица 8.1. В таблице отражены первые девять состояний регистра.
На каждом шаге все содержимое регистра сдвигается вправо на один разряд. При этом можно получить в качестве
результата один бит. На освободившееся слева место поступает бит, равный результату вычисления функции обратной
связи 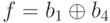 . Выходную последовательность генератора псевдослучайных бит образует последний столбец таблицы
(извлекаемый бит).
. Выходную последовательность генератора псевдослучайных бит образует последний столбец таблицы
(извлекаемый бит).
| Номер состояния | Внутреннее состояние регистра b4, b3, b2, b1 | Результат вычисления функции обратной связи 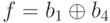 |
Извлекаемый бит ( b1 ) |
|---|---|---|---|
| 0 | 1 0 1 1 | 0 | 1 |
| 1 | 0 1 0 1 | 1 | 1 |
| 2 | 1 0 1 0 | 1 | 0 |
| 3 | 1 1 0 1 | 0 | 1 |
| 4 | 0 1 1 0 | 0 | 0 |
| 5 | 0 0 1 1 | 1 | 1 |
| 6 | 1 0 0 1 | 0 | 1 |
| 7 | 0 1 0 0 | 0 | 0 |
| 8 | 0 0 1 0 | 0 | 0 |
Линейный сдвиговый регистр размером n бит может находиться в одном из 2n-1 состояний (исключается состояние регистра из одних нулей - при появлении такого состояния далее будут порождаться лишь нули, и о псевдослучаности порождаемой последовательности говорить не приходится). Поэтому теоретически такой регистр может генерировать псевдослучайную последовательность с максимальным периодом 2n-1. Линейный сдвиговый регистр с обратной связью будет генерировать циклическую последовательность битов с максимальным периодом только при выборе в качестве отводной последовательности определенных бит. Разработана математическая теория, позволяющая выбрать подходящие номера разрядов для бит отводной последовательности.
Линейные сдвиговые регистры с обратной связью часто использовались и используются до сих пор при шифровании потоков данных. Для повышения криптостойкости в таких устройствах шифрования применяются комбинации нескольких сдвиговых регистров с обратной связью, а также вводятся дополнительные перемешивающие операции. Такие электронные схемы предлагались и выпускались еще до второй мировой войны. Аналогичные принципы заложены и в некоторые поточные шифры, созданные в конце XX века, например, в алгоритм А5, использовавшийся в Европе для шифрования сотовых цифровых каналов связи стандарта GSM. Несмотря на то, что некоторые криптоаналитики высказывают сомнения в надежности алгоритмов поточного шифрования с использованием линейных сдвиговых регистров с обратной связью, они положены в основу функционирования различных военных и гражданских устройств связи, используемых до настоящего времени.
Основным недостатком генераторов псевдослучайных чисел на базе линейных сдвиговых регистров является сложность программной реализации. Сдвиги и битовые операции легко и быстро выполняются в электронной аппаратуре, поэтому в разных странах выпускаются микросхемы и устройства для поточного шифрования на базе алгоритмов с использованием сдвиговых регистров с обратной связью.
Использование режимов OFB и CTR блочных шифров для получения псевдослучайных чисел
Можно использовать любой блочный алгоритм, например AES или ГОСТ 28147-89, для поточного шифрования информации, используя режимы OFB и CTR блочных шифров.
Название режима OFB (Output FeedBack) переводится как "обратная связь по выходу".
Пусть минимальный блок данных, используемый для передачи, состоит из j бит; обычным значением является j=8 (то есть минимальной порцией передаваемых данных является 1 байт). В режиме OFB блочный шифр f на основе секретного ключа К и некоторого инициализирующего значения Y0 формирует псевдослучайную последовательность j-битовых чисел z1,z2,...,zk, которая затем может использоваться в качестве гаммы для шифрования сообщения. Результат зашифрования является входом процедуры шифрования следующего блока исходного сообщения. На каждом этапе шифрования из зашифрованного блока Yi выбирается j младших битов.
Таким образом, для получения псевдослучайной последовательности используется схема:
Yi=f(Yi-1,K), zi=j младших бит Yi, 1<=i<=k
Если размер блока шифра равен N бит, то параметр j может принимать значения от 1 до N. Значение Y0 называют также инициализирующим вектором.
Последовательность чисел zi можно использовать в качестве гаммы для шифрования потока исходных данных, состоящего из символов хi:
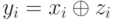
в результате чего получится поток зашифрованных символов yi.
Так как значения yi не зависят от открытого текста xi, то каждый раз, используя одни и те же параметры К и Y0, мы получим одну и ту же последовательность гаммы zi. Поэтому рекомендуется менять значение ключа К для передачи каждого нового сообщения.
Расшифрование сообщений для описанного режима может производиться только с начала последовательности, так как невозможно получить произвольный элемент последовательности zi, не вычислив все предыдущие.
Основное достоинство режима OFB заключается в том, что последовательность z может быть сформирована заранее для того, чтобы быстро шифровать или расшифровывать поточные сообщения в момент их поступления. Это может быть актуально для систем, обрабатывающих данные в реальном масштабе времени.
Еще одно важное достоинство режима OFB состоит в том, что если при передаче данных произошла ошибка, то она не распространяется на следующие зашифрованные блоки, и тем самым сохраняется возможность расшифрования последующих блоков. Например, если в результате передачи по зашумленному каналу связи появился ошибочный бит в блоке yi, то это приведет к невозможности расшифрования только этого блока и получения одного блока исходных данных xi. Дальнейшая последовательность блоков будет расшифрована корректно.
Название режима CTR происходит от слова "CounTeR" — "счетчик". Этот режим является модификацией режима OFB. Единственное отличие от OFB заключается в том, что в режиме CTR шифруется не предыдущий выход шифра, а счетчик, увеличиваемый на каждом шаге на 1. Первоначальное значение счетчика определяется некоторым инициализирующим значением Y0. Общая формула выглядит следующим образом:
Yi=f(Yi-1+1,K), zi=j старших бит Yi
Преимущество режима CTR состоит в том, что любой элемент последовательности z может быть вычислен непосредственно. Этот факт связан с тем, что на каждом шаге Yi увеличивается на единицу, и, следовательно, если нам известен номер шага i, то значение Yi можно вычислить непосредственно, зная Y0 и i по формуле:
Yi=f(Y0+i,K),
Это дает возможность шифровать и дешифровать любые фрагменты сообщения независимо друг от друга.