|
С помощью обобщенного алгоритма Евклида найдите числа х и у, удовлетворяющие уравнению 30х +12y = НОД(30,12). х=1, у=-2, НОД = 6. Где ошибка? |
Криптографические хеш-функции
Цель лекции: познакомиться с понятием "хеш-функция", а также с принципами работы таких функций.
Понятие хеш-функции
Хеш-функцией (hash function) называется математическая или иная функция, которая для строки произвольной длины вычисляет некоторое целое значение или некоторую другую строку фиксированной длины. Математически это можно записать так:
h=H(M),
где М – исходное сообщение, называемое иногда прообразом, а h – результат, называемый значением хеш-функции (а также хеш-кодом или дайджестом сообщения (от англ. message digest )).
Смысл хеш-функции состоит в определении характерного признака прообраза – значения хеш-функции. Это значение обычно имеет определенный фиксированный размер, например, 64 или 128 бит. Хеш-код может быть в дальнейшем проанализирован для решения какой-либо задачи. Так, например, хеширование может применяться для сравнения данных: если у двух массивов данных хеш-коды разные, массивы гарантированно различаются; если одинаковые — массивы, скорее всего, одинаковы. В общем случае однозначного соответствия между исходными данными и хеш-кодом нет из-за того, что количество значений хеш-функций всегда меньше, чем вариантов входных данных. Следовательно, существует множество входных сообщений, дающих одинаковые хеш-коды (такие ситуации называются коллизиями ). Вероятность возникновения коллизий играет немаловажную роль в оценке качества хеш-функций.
Хеш-функции широко применяются в современной криптографии.
Простейшая хеш-функция может быть составлена с использованием операции "сумма по модулю 2" следующим образом: получаем входную строку, складываем все байты по модулю 2 и байт-результат возвращаем в качестве значения хеш-фукнции. Длина значения хеш-функции составит в этом случае 8 бит независимо от размера входного сообщения.
Например, пусть исходное сообщение, переведенное в цифровой вид, было следующим (в шестнадцатеричном формате):
3E 54 A0 1F B4
Переведем сообщение в двоичный вид, запишем байты друг под другом и сложим биты в каждом столбике по модулю 2:
0011 1110 0101 0100 1010 0000 0001 1111 1101 0100 ---------- 0110 0101
Результат ( 0110 0101(2) или 65(16) ) и будет значением хеш-функции.
Однако такую хеш-функцию нельзя использовать для криптографических целей, например для формирования электронной подписи, так как достаточно легко изменить содержание подписанного сообщения, не меняя значения контрольной суммы.
Поэтому рассмотренная хеш-функция не годится для криптографических применений. В криптографии хеш-функция считается хорошей, если трудно создать два прообраза с одинаковым значением хеш-функции, а также, если у выхода функции нет явной зависимости от входа.
Сформулируем основные требования, предъявляемые к криптографическим хеш-функциям:
- хеш-функция должна быть применима к сообщению любого размера;
- вычисление значения функции должно выполняться достаточно быстро;
- при известном значении хеш-функции должно быть трудно (практически невозможно) найти подходящий прообраз М ;
- при известном сообщении М должно быть трудно найти другое сообщение М’ с таким же значением хеш-функции, как у исходного сообщения;
- должно быть трудно найти какую-либо пару случайных различных сообщений с одинаковым значением хеш-функции.
Создать хеш-функцию, которая удовлетворяет всем перечисленным требованиям – задача непростая. Необходимо также помнить, что на вход функции поступают данные произвольного размера, а хеш-результат не должен получаться одинаковым для данных разного размера.
В настоящее время на практике в качестве хеш-функций применяются функции, обрабатывающие входное сообщение блок за блоком и вычисляющие хеш-значение hi для каждого блока Mi входного сообщения по зависимостям вида
hi=H(Mi,hi-1),
где hi-1 – результат, полученный при вычислении хеш-функции для предыдущего блока входных данных.
В результате выход хеш-функции hn является функцией от всех n блоков входного сообщения.
Использование блочных алгоритмов шифрования для формирования хеш-функции
В качестве хеш-функции можно использовать блочный алгоритм симметричного шифрования. Если используемый блочный алгоритм криптографически стоек, то и хеш-функция на его основе будет надежной.
Простейшим способом использования блочного алгоритма для получения хеш-кода является шифрование сообщения в режиме CBC. В этом случае сообщение представляется в виде последовательности блоков, длина которых равна длине блока алгоритма шифрования. При необходимости последний блок дополняется справа нулями, чтобы получился блок нужной длины. Хеш-значением будет последний зашифрованный блок текста. При условии использования надежного блочного алгоритма шифрования полученное хеш-значение будет обладать следующими свойствами:
- практически невозможно без знания ключа шифрования вычисление хеш-значения для заданного открытого массива информации;
- практически невозможен без знания ключа шифрования подбор открытых данных под заданное значение хеш-функции.
Сформированное таким образом хеш-значение обычно называют имитовставкой или аутентификатором и используется для проверки целостности сообщения. Таким образом, имитовставка – это контрольная комбинация, зависящая от открытых данных и секретной ключевой информации. Целью использования имитовставки является обнаружение всех случайных или преднамеренных изменений в массиве информации. Значение, полученное хеш-функцией при обработке входного сообщения, присоединяется к сообщению в тот момент, когда известно, что сообщение корректно. Получатель проверяет целостность сообщения путем вычисления имитовставки полученного сообщения и сравнения его с полученным хеш-кодом, который должен быть передан безопасным способом. Одним из таких безопасных способов может быть шифрование имитовставки закрытым ключом отправителя, т.е. создание подписи. Возможно также шифрование полученного хеш-кода алгоритмом симметричного шифрования, если отправитель и получатель имеют общий ключ симметричного шифрования.
Указанный процесс получения и использования имитовставки описан в отечественном стандарте ГОСТ 28147-89. Стандарт предлагает использовать младшие 32 бита блока, полученного на выходе операции шифрования всего сообщения в режиме сцепления блоков шифра для контроля целостности передаваемого сообщения. Таким же образом для формирования имитовставки можно использовать любой блочный алгоритм симметричного шифрования.
Другим возможным способом применения блочного шифра для выработки хеш-кода является следующий. Исходное сообщение обрабатывается последовательно блоками. Последний блок при необходимости дополняется нулями, иногда в последний блок приписывают длину сообщения в виде двоичного числа. На каждом этапе шифруем хеш-значение, полученное на предыдущем этапе, взяв в качестве ключа текущий блок сообщения. Последнее полученное зашифрованное значение будет окончательным хеш-результатом.
Таким образом, если обычную схему шифрования сообщения М с помощью блочного шифра f на ключе К мы записывали как E=f(M,K), то схему получения хеш-кода h по описанному выше алгоритму можно представить как
hi=f(hi-1,M)
В качестве начального хеш-кода h0 берут некоторую константу. Шифрование производится в режиме простой замены. При использовании указанного способа размер блока совпадает с длиной ключа и размером хеш-значения будет длина блока.
Возможен также другой способ использования блочного шифра в режиме простой замены: элементы сообщения шифруются хеш-значениями, полученными на предыдущем этапе:
hi=f(M,hi-1)
На самом деле возможны еще несколько схем использования блочного шифра для формирования хеш-функции. Пусть Мi – блок исходного сообщения, hi – значение хеш-функции на i-том этапе, f – блочный алгоритм шифрования, используемый в режиме простой замены,  – операция сложения по модулю 2. Тогда возможны, например, следующие схемы формирования хеш-функции:
– операция сложения по модулю 2. Тогда возможны, например, следующие схемы формирования хеш-функции:
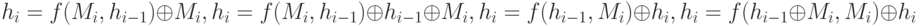
Во всех этих схемах длина формируемого хеш-значения равна длине блока при шифровании. Все эти, а также некоторые другие схемы использования блочного алгоритма шифрования для вычисления хеш-значений могут применяться на практике.
Основным недостатком хеш-функций, спроектированных на основе блочных алгоритмов, является относительно низкая скорость работы. Необходимую криптостойкость можно обеспечить и за меньшее количество операций над входными данными. Существуют более быстрые алгоритмы хеширования, спроектированных самостоятельно, с нуля, исходя из требований криптостойкости (наиболее распространенные из них – MD5, SHA-1, SHA-2 и ГОСТ Р 34.11-94).
