Изображение полиэдра
Работа с тенями от граней
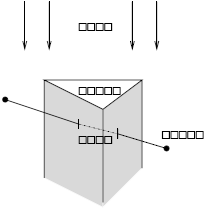
Так как плоское изображение полиэдра состоит из проекций видимых частей ребер, а изображать проекцию любого набора отрезков мы уже научились, то осталось только правильно учесть влияние теней от граней. Напомним, что хотя в программной реализации используется произвольно заданный вектор проектирования, в теоретических рассуждениях мы считаем его направленным вертикально вверх. Плоскость, на которой изображается полиэдр, при этом оказывается горизонтальной.
Если предположить, что бесконечно высоко расположен источник света, то на каждом ребре образуются освещенные и затененные участки. Первые мы будем называть просветами, а вторые — тенями. Рисунок 13.4 иллюстрирует эти понятия.
Для получения изображения видимой части ребра нужно учесть тени от всех граней полиэдра, а затем изобразить все оставшиеся просветы. Ключевым аспектом решения данной задачи будет являться формализация понятия тень от грани на ребро. Подробнее вопрос ее определения будет рассмотрен ниже, а пока заметим, что тень любой грани на ребре всегда представляет собой отрезок, если только она не пуста.
Важным наблюдением, существенно упрощающим искомый алгоритм, является тот факт, что задача нахождения теней и просветов на конкретном ребре — одномерная. Сопоставив началу ребра координату 0, а концу — 1, мы можем установить взаимно однозначное соответствие между трехмерными координатами точек ребра и введенными одномерными координатами. После этого каждый из просветов будет представлять собой отрезок, а реализовывать его будет класс Segment, в каждом экземпляре которого должны храниться одномерные координаты начала и конца обрабатываемого отрезка. Методы данного класса обязаны обеспечить все необходимые действия с отрезками, которые понадобятся при определении множества просветов.
public class Segment {
private double begin, end;
public Segment(double begin, double end) {
this.begin = begin; this.end = end;
}
public final boolean degenerate() {
return begin >= end;
}
public final Segment leftSub(Segment s) {
return new Segment(begin, Math.min(end, s.begin));
}
public final Segment rightSub(Segment s) {
return new Segment(Math.max(begin, s.end), end);
}
public final Segment intersection(Segment s) {
begin = Math.max(begin, s.begin);
end = Math.min(end, s.end);
return this;
}
public final double getBegin() {
return begin;
}
public final double getEnd() {
return end;
}
}Указанные действия включают в себя проверку вырожденности отрезка
(метод degenerate ), а также вычисление пересечения двух отрезков и определения
обеих компонент разности двух отрезков. Отрезок ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) является
вырожденным,
если он представляет из себя точку или пустое множество, то есть если
является
вырожденным,
если он представляет из себя точку или пустое множество, то есть если 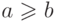 . Пересечение двух отрезков всегда является отрезком
(возможно,
вырожденным), который вычисляется в методе intersection, а разность двух
отрезков всегда состоит из двух отрезков, каждый из которых может
оказаться вырожденным. Левая и правая компоненты разности вычисляются с
помощью методов leftSub и rightSub соответственно.
. Пересечение двух отрезков всегда является отрезком
(возможно,
вырожденным), который вычисляется в методе intersection, а разность двух
отрезков всегда состоит из двух отрезков, каждый из которых может
оказаться вырожденным. Левая и правая компоненты разности вычисляются с
помощью методов leftSub и rightSub соответственно.
Совокупность всех просветов ребра целесообразно хранить в односвязном списке
сегментов, для чего будем использовать изученную нами ранее ссылочную
реализацию (класс L1ListSegments ). В самом начале обработки очередного
ребра множество просветов состоит из одного элемента, совпадающего со
всем ребром, — отрезка ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) . Последовательный учет теней от
граней
можно считать функцией на пространстве последовательности граней. Легко
заметить, что эта функция индуктивна — зная список просветов, который
учитывает тени от нескольких граней, и тень от еще одной, новой грани,
легко вычислить новый список просветов, учитывающий и тень от новой грани.
Для этого достаточно для всех просветов вычислить их разности с отрезком
тени от грани (см. рис. 13.5).
. Последовательный учет теней от
граней
можно считать функцией на пространстве последовательности граней. Легко
заметить, что эта функция индуктивна — зная список просветов, который
учитывает тени от нескольких граней, и тень от еще одной, новой грани,
легко вычислить новый список просветов, учитывающий и тень от новой грани.
Для этого достаточно для всех просветов вычислить их разности с отрезком
тени от грани (см. рис. 13.5).
В зависимости от расположения отрезков, соответствующих просвету и тени, их разность может оказаться пустой (если просвет целиком попал в тень), состоящей из единственной точки, двух точек, одного отрезка, точки и отрезка, и двух отрезков. Как это уже обсуждалось ранее, мы не будем различать эти ситуации. Гораздо удобнее считать, что разность всегда состоит из двух отрезков, каждый из которых может быть вырожденным.
Приведем ту часть реализации класса ShadowDrawer, которая уже обсуждена нами.
public class ShadowDrawer extends SimpleDrawer {
protected R3Vector begin;
protected R3Vector end;
private static final int MAXSIZE = 128;
private L1ListSegments list;
private static final double t0 = 0.;
private static final double t1 = 1.;
private R3Vector R3(double t) {
return R3Vector.plus( R3Vector.mul((1.-t), begin),
R3Vector.mul(t, end) );
}
protected final void addShadow(Facet f) {
try {
Segment s = shadow(f);
if (!s.degenerate()) {
list.toFront();
while (!list.end()) {
Segment next = list.erase();
Segment left = next.leftSub(s);
if (!left.degenerate()) {
list.insert(left);
list.forward();
}
Segment right = next.rightSub(s);
if (!right.degenerate()) {
list.insert(right);
list.forward();
}
}
}
} catch(Exception e) {
Xterm.println("Слишком много видимых отрезков ребра.");
System.exit(0);
}
}
protected void addShadow() {
for(int j=0; j<p.getFacetsQuantity(); j++)
addShadow(p.getFacet(j));
}
public ShadowDrawer(Polyedr p, R3Vector pr, double angle) {
super(p, pr, angle);
list = new L1ListSegments(MAXSIZE);
}
public final void drawEdge(Edge s) {
begin = s.getBegin();
end = s.getEnd();
list.clear();
try {
list.insert(new Segment(t0, t1));
} catch(Exception e) {;}
addShadow();
try {
for (list.toFront(); ! list.end(); list.forward()) {
Segment u = list.after();
R3Vector begin = R3(u.getBegin());
R3Vector end = R3(u.getEnd());
draw(xnProection(begin), ynProection(begin),
xnProection(end), ynProection(end));
}
} catch(Exception e) {;}
Xterm.print(".");
}
}