Спецификация программ и преобразователь предикатов
Вычисление слабейшего предусловия
Покажем на ряде примеров, как решаются задачи на вычисление слабейшего предусловия.
Задача 6.9. Вычислите и упростите 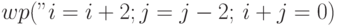 .
.
Решение.
Для вычисления воспользуемся определениями слабейшего предусловия для
последовательного выполнения операторов и оператора присваивания. Так как
в данном случае все выражения заведомо являются определенными, то истинный
предикат  будет опущен изначально.
будет опущен изначально.
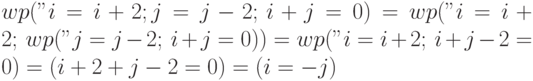 .
.
Задача 6.10. Вычислите и упростите  .
.
Решение. 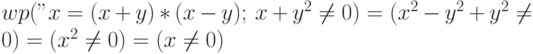 .
.
Задача 6.11. Вычислите и упростите  .
.
Решение.
В данном случае ответ  является ошибочным, так как
является ошибочным, так как  .
.
Задача 6.12. Вычислите и упростите ![wp("i=1; s=b[0];",
1 \leqslant i < n \ \land \ s = b[0]+\ldots+b[i-1] )](/sites/default/files/tex_cache/64aebcd8d5b6e2425396093c4594f73b.png) .
.
Решение.
![wp("i=1; s=b[0];", 1 \leqslant i < n \ \land \ s =
b[0]+\ldots+b[i-1] ) =\\
wp("i=1;", wp("s=b[0];", 1 \leqslant i < n \ \land \ s =
b[0]+\ldots+b[i-1])) =
wp("i=1;", 1 \leqslant i < n \ \land \ b[0] =
b[0]+\ldots+b[i-1]) = \\
( 1 \leqslant 1 < n \land (b[0] =
b[0])) = (1<n \land (b[0] = b[0])) = (n>1).](/sites/default/files/tex_cache/5626bd5b9a5f7c341ce86ab28173895f.png)
Задача 6.13. Вычислите и упростите  для произвольного предиката
для произвольного предиката  .
.
Решение.
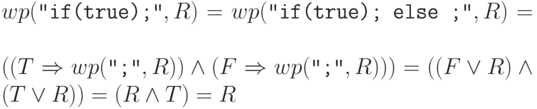
Рассмотрим в заключение задачу на решение уравнения, связанного со слабейшим предусловием.
Задача 6.14. Найдите такое значение выражения  , включающее другие переменные,
для которого спецификация
, включающее другие переменные,
для которого спецификация 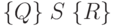 становится тавтологией:
становится тавтологией:  .
.
Решение.
Вспомним, что имеет место эквивалентность  . Таким образом, нам
необходимо
подобрать такое
. Таким образом, нам
необходимо
подобрать такое  , для которого
, для которого 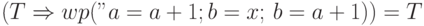 . Вычислим сначала
слабейшее предусловие, входящее в этот предикат:
. Вычислим сначала
слабейшее предусловие, входящее в этот предикат:

Легко убедиться, однако, что мы получили неверный результат! И все дело в
том, что переменная  зависит от
зависит от  . Проведем
вычисления повторно,
заменив
. Проведем
вычисления повторно,
заменив  на
на 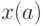 :
:  .
.
Вернемся к исходной задаче. Нам нужно выяснить, при каких значениях  выражение
выражение 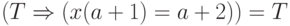 окажется
тавтологией. Упростим
данное выражение:
окажется
тавтологией. Упростим
данное выражение:

Теперь ответ очевиден:  или просто
или просто 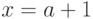 .
.
Задачи для самостоятельного решения
Задача 6.15. Запишите предикат, утверждающий, что
самое большее одно из следующих утверждений истинно:  ,
,  .
.
Задача 6.16. Запишите предикат, утверждающий, что
следующие утверждения не являются истинными одновременно:  ,
,  и
и 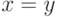 .
.
Задача 6.17. Запишите предикат, утверждающий следующее:
когда 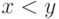 ,
,  означает, что
означает, что  , но если
, но если  , то
, то  не может выполняться; однако если
не может выполняться; однако если  , то
, то 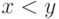 .
.
Задача 6.18. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины 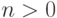 все нули массива находятся в вырезке
все нули массива находятся в вырезке ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) .
.
Задача 6.19. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины 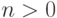 некоторые нули массива находятся в вырезке
некоторые нули массива находятся в вырезке ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) .
.
Задача 6.20. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины 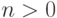 справедливо высказывание:
неверно, что все нули массива находятся в вырезке
справедливо высказывание:
неверно, что все нули массива находятся в вырезке ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) .
.
Задача 6.21. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины 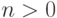 справедливо высказывание:
неверно, что не все нули массива находятся в вырезке
справедливо высказывание:
неверно, что не все нули массива находятся в вырезке ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) .
.
Задача 6.22. Запишите предикат, который утверждает, что функция 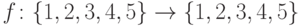 является инъективной и отрицание этого факта.
Упростите получившиеся предикаты, если это возможно.
является инъективной и отрицание этого факта.
Упростите получившиеся предикаты, если это возможно.
Задача 6.23. Запишите предикат, который утверждает, что функция 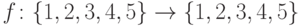 является биективной и отрицание этого факта.
Упростите получившиеся предикаты, если это возможно.
является биективной и отрицание этого факта.
Упростите получившиеся предикаты, если это возможно.
Задача 6.24. Запишите предикат, который утверждает, что функция 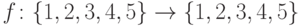 все существует единственный элемент
все существует единственный элемент  , который функция
, который функция  уменьшает, и отрицание
этого факта. Не используйте при этом квантора
уменьшает, и отрицание
этого факта. Не используйте при этом квантора  !.
!.
Задача 6.25. Основываясь на определении 6.4 и спецификации
программы 6.1, докажите истинность эквивалентности  .
.
Задача 6.26. Основываясь на определении 6.4,
докажите закон монотонности  .
.
Задача 6.27. Основываясь на определении 6.4,
докажите закон дистрибутивности дизъюнкции  .
.
Задача 6.28. Вычислите и упростите  .
.
Задача 6.29. Вычислите и упростите  .
.
Задача 6.30. Вычислите и упростите 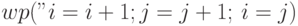 .
.
Задача 6.31. Вычислите и упростите 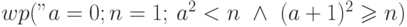 .
.
Задача 6.32. Вычислите и упростите ![wp("s=s+b[i]; i=i+1;", 0<i<n\ \land\ s=b[0]+\ldots+b[i-1])](/sites/default/files/tex_cache/549f5c9a95af97ae6f7ea9b1a07b0802.png) .
.
Задача 6.33. Вычислите и упростите следующее слабейшее предусловие  .
.
Задача 6.34. Найдите такое значение выражения  , включающее другие переменные,
для которого спецификация
, включающее другие переменные,
для которого спецификация 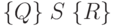 становится тавтологией:
становится тавтологией:  .
.
Задача 6.35. Найдите такое значение выражения  , включающее другие переменные,
для которого спецификация
, включающее другие переменные,
для которого спецификация 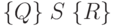 становится тавтологией:
становится тавтологией: 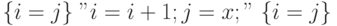 .
.
