Спецификация программ и преобразователь предикатов
Спецификация программы и преобразователь предикатов wp
Для того чтобы доказывать правильность программ необходимо прежде всего дать строгое определение понятию правильная программа. Ясно, что оно зависит не только от результата, который должен быть получен в процессе выполнения программы, но и от того, в каких условиях начинается ее выполнение.
Определение 6.1. Спецификацией 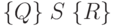 программы
программы  ,
где
,
где  и
и  — предикаты, называется предикат, означающий,
что если выполнение
— предикаты, называется предикат, означающий,
что если выполнение  началось в состоянии, удовлетворяющем
началось в состоянии, удовлетворяющем  , то имеется гарантия, что
оно
завершится через конечное время в состоянии, удовлетворяющем
, то имеется гарантия, что
оно
завершится через конечное время в состоянии, удовлетворяющем  .
.
Под программой  в данном определении может пониматься один
или несколько
отдельных операторов или же действительно целая большая программа.
в данном определении может пониматься один
или несколько
отдельных операторов или же действительно целая большая программа.
Определение 6.2.
Предикат  называется предусловием или входным
утверждением
называется предусловием или входным
утверждением  ;
;  — постусловием или выходным утверждением программы
— постусловием или выходным утверждением программы  .
.
Так как спецификация программы является предикатом, то она может быть истинной, а может быть и ложной. Возможна и такая ситуация, когда в некоторых состояниях она истинна, а в других — ложна. Вот соответствующие примеры.
Спецификация 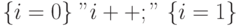 является
тавтологией,
спецификация
является
тавтологией,
спецификация 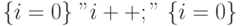 ложна во всех
состояниях,
а спецификация
ложна во всех
состояниях,
а спецификация 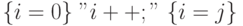 истинна при
истинна при  и ложна
в остальных состояниях.
и ложна
в остальных состояниях.
Спецификация программы является единственным корректным способом постановки задачи. Только четко сформулировав пред- и постусловия, можно обсуждать затем правильность программы.
Определение 6.3.
Программа  является правильной при заданных
является правильной при заданных  и
и  ,
если спецификация
,
если спецификация 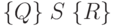 является тавтологией.
является тавтологией.
С практической точки зрения особый интерес представляют программы, которые позволяют получить нужный результат при минимальных требованиях к начальным условиям, а также программы, позволяющие достичь как можно большего при фиксированном предусловии.
Слабейшее предусловие — предикат, описывающий максимально широкое
множество в пространстве состояний переменных программы  , на
котором
гарантируется получение постусловия
, на
котором
гарантируется получение постусловия  . Сильнейшее
постусловие
— предикат, описывающий максимально сильные ограничения на состояние
переменных программы
. Сильнейшее
постусловие
— предикат, описывающий максимально сильные ограничения на состояние
переменных программы  , которые могут быть получены при данном
предусловии
, которые могут быть получены при данном
предусловии  .
.
Для целей доказательства правильности программ особенно важен следующий предикат.
Определение 6.4. Слабейшее предусловие  — предикат, представляющий
множество
всех состояний переменных программы
— предикат, представляющий
множество
всех состояний переменных программы  , для которых выполнение
команды
, для которых выполнение
команды  ,
начавшееся в таком состоянии, обязательно закончится через конечное время в
состоянии, удовлетворяющем
,
начавшееся в таком состоянии, обязательно закончится через конечное время в
состоянии, удовлетворяющем  .
.
Проиллюстрируем введенное понятие на нескольких примерах.
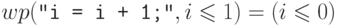 , так как если
переменная
, так как если
переменная  удовлетворяла условию
удовлетворяла условию  , то
после выполнения
программы
, то
после выполнения
программы 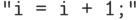 она действительно будет удовлетворять
неравенству
она действительно будет удовлетворять
неравенству  .
.
 , ибо
выполнение программы
, ибо
выполнение программы  при любых начальных условиях приведет к тому, что переменная
при любых начальных условиях приведет к тому, что переменная  станет равной максимальному значению из величин
станет равной максимальному значению из величин  и
и  .
.
 ,
потому что
,
потому что  будет равно максимуму из чисел
будет равно максимуму из чисел  и
и  (а именно
таково будет
(а именно
таково будет  после выполнения программы
после выполнения программы  ) тогда и только тогда, если
именно
переменная
) тогда и только тогда, если
именно
переменная  имеет большее значение.
имеет большее значение.
 . Это (пустое
множество
состояний) означает, что ни при каких начальных условиях программа
. Это (пустое
множество
состояний) означает, что ни при каких начальных условиях программа  не сможет сделать величину
не сможет сделать величину  меньше,
чем
меньше,
чем  .
.
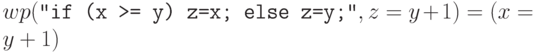 , ибо
только при
таком начальном условии после выполнения приведенной программы переменная
, ибо
только при
таком начальном условии после выполнения приведенной программы переменная  станет равной
станет равной  .
.
Заметим, что из определений спецификации программы и ее слабейшего предусловия вытекает следующее утверждение.
Предложение 6.1.  .
.
Определение 6.5. Преобразователем предикатов (обозначаемый через 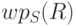 )
называют
)
называют  когда фиксируют программу
когда фиксируют программу  и рассматривают
и рассматривают  как функцию
одной переменной
как функцию
одной переменной  .
.
Предложение 6.2.
Преобразователь предикатов  обладает следующими
свойствами:
обладает следующими
свойствами:
1) 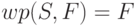 (закон исключенного чуда);
(закон исключенного чуда);
2) 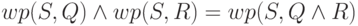 (дистрибутивность
конъюнкции);
(дистрибутивность
конъюнкции);
3)  (закон монотонности);
(закон монотонности);
4) 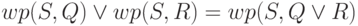 (дистрибутивность дизъюнкции).
(дистрибутивность дизъюнкции).
Величина  описывает такое множество начальных условий,
при которых
выполнение программы
описывает такое множество начальных условий,
при которых
выполнение программы  завершится через конечное время в
состояний,
удовлетворяющем
завершится через конечное время в
состояний,
удовлетворяющем  , то есть ни в каком состоянии. Этого, конечно,
быть не
может, что и поясняет название свойства — закон исключенного чуда.
, то есть ни в каком состоянии. Этого, конечно,
быть не
может, что и поясняет название свойства — закон исключенного чуда.
Докажем аккуратно дистрибутивность конъюнкции. Для доказательства
эквивалентности достаточно показать, что из условия 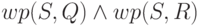 ,
стоящего в левой части, вытекает условие
,
стоящего в левой части, вытекает условие 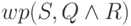 ,
размещенное в
правой, и наоборот. Для доказательства импликации
,
размещенное в
правой, и наоборот. Для доказательства импликации 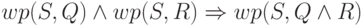 рассмотрим
произвольное
состояние
рассмотрим
произвольное
состояние  , удовлетворяющее условию
, удовлетворяющее условию 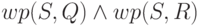 . Так как
выполнение программы
. Так как
выполнение программы  , начавшееся в
, начавшееся в  , завершится
при истинных
, завершится
при истинных  и
и  ,
то истинным будет и предикат
,
то истинным будет и предикат 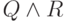 .
.
Для доказательства обратной импликации 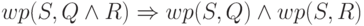 рассмотрим состояние
рассмотрим состояние  , удовлетворяющее условию
, удовлетворяющее условию 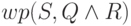 . Тогда
выполнение
. Тогда
выполнение  , начавшееся в
, начавшееся в  , обязательно завершится
в некотором
состоянии
, обязательно завершится
в некотором
состоянии 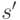 , удовлетворяющем
, удовлетворяющем 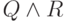 . Но любое
такое
. Но любое
такое 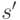 обязательно
удовлетворяет и
обязательно
удовлетворяет и  и
и  , так что
, так что  удовлетворяет и
удовлетворяет и  и
и  ,
что и завершает доказательство.
,
что и завершает доказательство.
Закон монотонности докажите самостоятельно, а вот по поводу последнего
свойства преобразователя предикатов — дистрибутивности дизъюнкции —
надо сделать некоторые замечания. Дело в том, что если в качестве  рассмотреть операцию бросания монеты, которая может завершиться либо выпадением
герба (
рассмотреть операцию бросания монеты, которая может завершиться либо выпадением
герба (  ), либо решки (
), либо решки (  ), то
), то 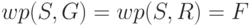 , ибо нельзя
гарантированно предсказать результат бросания ни при каких начальных условиях.
С другой стороны,
, ибо нельзя
гарантированно предсказать результат бросания ни при каких начальных условиях.
С другой стороны, 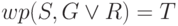 , так как всегда выпадет
либо герб,
либо решка.
, так как всегда выпадет
либо герб,
либо решка.
Если  является недетерминированной, то эквивалентность
в законе дистрибутивности дизъюнкции превращается в импликацию. Однако
для программ
является недетерминированной, то эквивалентность
в законе дистрибутивности дизъюнкции превращается в импликацию. Однако
для программ  , реализованных с помощью большинства языков
программирования,
подобная ситуация невозможна.
, реализованных с помощью большинства языков
программирования,
подобная ситуация невозможна.
