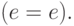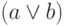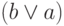Высказывания и предикаты
Семантика предикатов
В предыдущей секции мы разобрались с синтаксисом языка предикатов.
Теперь нужно обсудить семантику этого языка, то есть придать смысл
каждой из цепочек, ему принадлежащих. Иными словами, нам необходимо придать
смысл каждому из предикатов. Сделаем это в три этапа, рассмотрев сначала
простейшие предикаты  и
и  , затем константные
предикаты, а уж затем
определим значение произвольного высказывания.
, затем константные
предикаты, а уж затем
определим значение произвольного высказывания.
Определение 3.10.
Предикат  имеет значение
имеет значение  ( Ложь ), а
предикат
( Ложь ), а
предикат  —
значение
—
значение  ( Истина ).
( Истина ).
Определение 3.11. Назовем предикат константным, если в нем не содержится ни одного идентификатора. Значение любого такого предиката находится с помощью таблицы истинности 3.2 и дерева вывода для него.
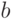 |
 |
 |
 |
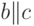 |
 |
 |
 |
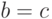 |
|---|---|---|---|---|---|---|---|---|
| T | T | F | T | T | T | T | T | T |
| T | F | F | T | T | F | F | F | F |
| F | T | T | T | T | F | F | T | F |
| F | F | T | F | F | F | F | T | T |
Рассмотрим, например, константный предикат  .
Изобразим дерево вывода для него и будем, двигаясь снизу вверх, заменять
результаты операций в соответствии с таблицей истинности, пока не дойдем
до самого корня дерева. Это последнее значение и будет считаться значением
предиката (см. рис. 3.2).
.
Изобразим дерево вывода для него и будем, двигаясь снизу вверх, заменять
результаты операций в соответствии с таблицей истинности, пока не дойдем
до самого корня дерева. Это последнее значение и будет считаться значением
предиката (см. рис. 3.2).
Для задания семантики предиката, содержащего переменные, нам необходимо следующее определение состояния.
Определение 3.12. Состояние  — это отображение из множества
идентификаторов
в множество {
— это отображение из множества
идентификаторов
в множество {  ,
,  }. Пространство состояний
переменных программы —
это прямое произведение множеств состояний всех переменных программы.
}. Пространство состояний
переменных программы —
это прямое произведение множеств состояний всех переменных программы.
Теперь можно дать определение значения любого предиката в заданном состоянии.
Определение 3.13. Значение предиката  в состоянии
в состоянии  (записывается как
(записывается как 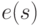 или
или  ) совпадает со значением константного предиката, который
получается из
предиката
) совпадает со значением константного предиката, который
получается из
предиката  заменой всех идентификаторов на их значения в
состоянии
заменой всех идентификаторов на их значения в
состоянии  .
.
Предикат  , например, в состоянии
, например, в состоянии  имеет значение
имеет значение  , ибо именно таково значение
константного
предиката
, ибо именно таково значение
константного
предиката 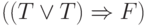 .
.
Из таблицы истинности следует, что операции дизъюнкции 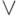 и
условного Или
и
условного Или 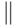 , а также конъюнкции
, а также конъюнкции 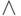 и
условного И
и
условного И 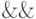 попарно эквивалентны. Это действительно так, но только до тех пор, пока мы
остаемся в рамках действия определения 3.12. Для нужд описания
реального мира, однако, полезно его несколько ослабить и разрешить некоторым
переменным оставаться неопределенными.
попарно эквивалентны. Это действительно так, но только до тех пор, пока мы
остаемся в рамках действия определения 3.12. Для нужд описания
реального мира, однако, полезно его несколько ослабить и разрешить некоторым
переменным оставаться неопределенными.
Определение 3.14. Состояние  в расширенном смысле — отображение из
множества
идентификаторов в множество {
в расширенном смысле — отображение из
множества
идентификаторов в множество {  ,
,  ,
,  }, где символ
}, где символ  означает
неопределенное (undefined) значение.
означает
неопределенное (undefined) значение.
Большинство предикатов не имеют определенного значения в таком состоянии,
в котором не определены некоторые из переменных, входящих в него. В частности,
операции 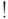 ,
, 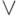 ,
, 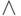 ,
,  и
и  дают результат
дают результат  , если
хотя бы один из операндов имеет значение
, если
хотя бы один из операндов имеет значение  . Совершенно другая
ситуация с
условными операторами. Для них справедлива таблица истинности 3.3.
. Совершенно другая
ситуация с
условными операторами. Для них справедлива таблица истинности 3.3.
| b | T | T | F | F | T | F | U | U | U |
| c | T | F | T | F | U | U | T | F | U |
| b || c | T | T | T | F | T | U | T | U | U |
| b&&c | T | F | F | F | U | F | U | U | U |
Среди огромного множества всех предикатов особую роль играют те из них,
которые всегда являются истинными, как, например 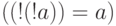 .
.
Определение 3.15. Предикат называется тавтологией, если он истинен во всех состояниях, в которых он определен.
Один из простейших способов доказать, что предикат является тавтологией, —
это вычислить его значения во всех возможных состояниях.
Таблица 4 является доказательством
того факта, что предикат  — тавтология.
— тавтология.
Определение 3.16.
Высказывания  и
и 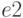 эквивалентны, если
предикат
эквивалентны, если
предикат  является
тавтологией.
является
тавтологией.
Использование законов эквивалентности дает возможность упрощать предикаты, что часто бывает весьма полезно. Докажите самостоятельно, что все перечисленные ниже законы эквивалентности действительно являются тавтологиями.
Предложение 3.2. Законы коммутативности:

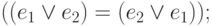

Предложение 3.3. Законы ассоциативности:



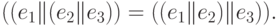
Предложение 3.4. Законы дистрибутивности:




Предложение 3.5.Законы де Моргана:

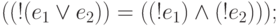


Предложение 3.6. Закон отрицания:
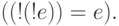
Предложение 3.7. Законы исключенного третьего:
 ;
;
 , если
, если  определено.
определено.
Предложение 3.8. Законы противоречия:
 ;
;
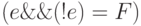 , если
, если  определено.
определено.
Предложение 3.9. Закон импликации:

Предложение 3.10. Закон равенства:

Предложение 3.11. Законы упрощения дизъюнкции:

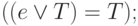


Предложение 3.12. Законы упрощения конъюнкции:
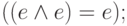
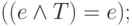
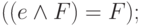
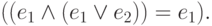
Предложение 3.13. Законы упрощения условного Или:
 ;
;
 , если
, если  определено;
определено;
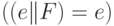 ;
;
 .
.
Предложение 3.14. Законы упрощения условного И:
 ;
;
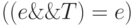 ;
;
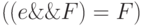 , если
, если  определено;
определено;
 .
.
Предложение 3.15. Закон тождества: