Поиск

Логарифмический поиск в динамических таблицах

Здесь мы рассмотрим организацию в виде деревьев для таблиц, в которых часто встречаются включения и исключения. Что происходит с временем поиска в дереве, которое модифицировалось путем включения и исключения? Если включенные и исключенные имена выбраны случайно, то оказывается, что в среднем время поиска мало изменяется; но в худшем случае поведение плохое - деревья могут вырождаться в линейные списки, поиск в которых нужно осуществлять последовательно. Проблема вырождения дерева в линейный список, приводящая к времени поиска 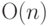вместо в практических применениях выражена более резко, чем это указывается теоретическим анализом. Такой анализ обычно предполагает, что включения и исключения появляются случайным образом, но на практике часто это не так.

Случайные деревья бинарного поиска. Как ведут себя деревья бинарного поиска без ограничений в качестве динамических деревьев? Другими словами, предположим, что дерево бинарного поиска меняется при случайных включениях и исключениях.

Для включения мы используем незначительную модификацию алгоритма 13.5. Если не было найдено, мы получаем для новую ячейку и связываем ее с последним узлом, пройденным во время безуспешного поиска . Соответствующее предложение нельзя однако просто добавить в конце алгоритма 13.5, поскольку при нормальном окончании цикла 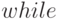указатель не указывает больше на последний пройденный узел, а вместо этого имеет значение . В связи с этим мы должны производить включение до того, как выполняется предположение 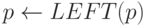или 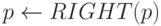; мы можем осуществить это, сделав процедуру включения рекурсивной. Процедура 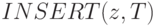выдает в качестве значения указатель на дерево, в которое добавлено . Таким образом, используется для включения в .

Алгоритм 13.6. Включение в дерево бинарного поиска

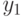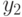Исключение гораздо сложнее включения, и мы изложим здесь только основную идею. Если подлежащее удалению имя имеет самое большее одного сына, то при исключении его сын (если он вообще есть) объявляется сыном отца . Если имеет двух сыновей, его прямо удалить нельзя. Вместо этого мы находим в таблице либо имя , которое непосредственно предшествует , либо имя , которое непосредственно следует за в естественном порядке. Оба имени принадлежат узлам, которые имеют не больше одного сына, и, таким образом, можно исключить заменой его либо именем 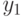, либо 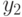, и затем исключением узла, который содержал 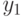или 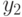, соответственно.

Сбалансированные сильно ветвящиеся деревья

Деревья бинарного поиска естественным образом обобщаются до -арных деревьев поиска, в которых каждый узел имеет сыновей и содержит имен. Имена в узле делят множество имен на подмножеств, каждое подмножество соответствует одному из поддеревьев узла. На рис. 13.2 показано полностью заполненное 5-арное дерево с двумя уровнями. Заметим, что мы не можем требовать, чтобы каждый узел -арного дерева имел ровно сыновей и включал равно 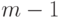имен; если мы захотим включить в дерево на рисунке 13.2, то должны будем создать узлы с меньше чем сыновьями и меньше чем 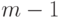именами. Таким образом, определение -арного дерева утверждает только, что каждый узел имеет не более сыновей и содержит не более 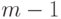имен. Ясно, что на -арных деревьях можно осуществлять поиск так же, как и на бинарных деревьях.

Как и в деревьях бинарного поиска, полезно различать внутренние узлы и листья. Внутренний узел содержит 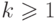имен, записанных в естественном порядке, и имеет сыновей, каждый из которых может быть либо внутренним узлом, либо листом. Лист не содержит имен (разве что временно в процессе включения), и, как раньше, в листьях - завершаются безуспешные поиски. Обычно за очевидностью мы на рисунке их опускаем.

Рис. 13.2. Абсолютно сбалансированное, полностью заполненное 5-арное дерево поиска

Сбалансированное сильно ветвящееся дерево порядка есть -арное дерево в котором:

1. Все листья расположены на одном уровне.
2. Корень имеет сыновей, .
3. Другие внутренние узлы имеют 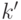сыновей, .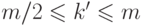