НОУ ИНТУИТ | Классические и квантовые вычисления. Лекция 10: Физически реализуемые преобразования матриц плотности

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 15.03.2007 | Уровень: профессионал | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 11 студентам

| Поделиться |

Поддержать программу

Измерение

При описании квантовых алгоритмов часто бывает естественно считать, что наряду с квантовым вычислительным устройством используется и классическое. Основной механизм взаимодействия между квантовой и классической частями состоит в измерении квантовых регистров, дающем классический результат.

Рассмотрим систему, состоящую из двух частей, — квантовой ( $\calN$ ) и классической ( $\calK$ ). По классическим координатам матрица плотности диагональна:

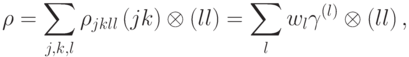
$\rho=\sum_{j,k,l}^{} \rho_{jkll} \left( \ket{j}\bra{k} \right)\otimes\left( \ket{l}\bra{l} \right)= \sum_{l}^{} w_l \gamma^{(l)} \otimes\left(\ket{l}\bra{l}\right),$

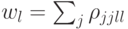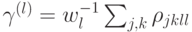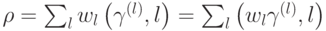где $w_l=\sum_j\rho_{jjll}$ — вероятность иметь классическое состояние , а оператор $\gamma^{(l)}=w_l^{-1}\sum_{j,k}\rho_{jkll}$ обладает всеми свойствами матрицы плотности. Таким образом, квантово-классическое состояние всегда разложимо на "условные" (по аналогии с условными вероятностями) матрицы плотности $\gamma^{(l)}$ . Будем использовать для такого случая специальное обозначение: $\rho=\sum_{l}w_l\left(\gamma^{(l)},l\right)= \sum_{l}\left(w_l\gamma^{(l)},l\right)$ .

Пусть имеется ряд взаимоисключающих возможностей, что выражается разложением пространства состояний в прямую сумму попарно ортогональных подпространств

$\calN=\bigoplus\limits_{j\in\Omega}\calL_j,$

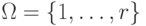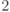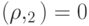где $\Omega=\{1,\dots,r\}$ — множество возможностей (действительно, если подпространство $\calL_1$ ортогонально подпространству $\calL_2$ , то для любой матрицы плотности $\rho\in\DD(\calL_1)$ выполняется $\PP(\rho,\calL_2)=0$ ).

Преобразование матриц плотности, которое мы будем называть измерением, состоит в том, что для состояний из подпространства $\calL_j$ "измеряющий прибор" помещает в классический регистр номер состояния :

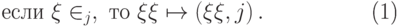$\begin{equation}\label{изм-чист} \text{если } \ket\xi\in\calL_j, \text{ то } \ket\xi\bra\xi\mapsto\left(\ket\xi\bra\xi,j\right). \end{equation}$

( 10.2)

Хотя измерение отображает пространство $\LL(\calN)$ в $\LL(\calN\otimes\calK)$ , результат всегда диагонален по второй компоненте. Поэтому можно считать, что измерение отображает $\LL(\calN)$ в $\bigoplus\limits_{j=1}\limits^{r} \LL(\calN)$ .

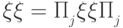Для $\ket{\xi}\in\calL_j$ выполняется равенство $\ket\xi\bra\xi= \Pi_{\calL_j}\ket\xi\bra\xi\Pi_{\calL_j}$ . Поэтому из соображений линейности можно доопределить измерение на всех остальных матрицах плотности

$\rho\ \mapsto\ \sum_{j}^{}\left(\Pi_{\calL_j}\rho\Pi_{\calL_j}, j\right)$

и прийти к следующему определению.

Определение 10.1. (Детерминированным) измерением называется преобразование матриц плотности

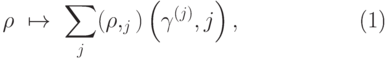$\begin{equation}\label{изм-общ} \rho\ \mapsto\ \sum_{j}^{}\PP(\rho,\calL_j)\left(\gamma^{(j)},j\right), \end{equation}$

( 10.3)

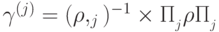где $\gamma^{(j)}=\PP(\rho,\calL_j)^{-1}\times\Pi_{\calL_j} \rho\Pi_{\calL_j}$ .

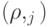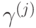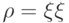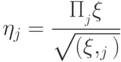Можно сказать, что — это результат измерения, $\PP(\rho,\calL_j)$ — вероятность получить данный результат, а $\gamma^{(j)}$ — состояние измеряемой системы после измерения при условии, что получен результат . Если мы измеряем чистые состояния, т.е. $\rho=\ket\xi\bra\xi$ , то $\gamma^{(j)}=\ket{\eta_j}\bra{\eta_j}$ , где $\displaystyle \ket{\eta_j}=\frac{\Pi_{\calL_j}\ket\xi}{\sqrt{\PP(\ket\xi,\calL_j)}}$ .

Приведем простейший пример измерения. Сделаем две копии бита. Пусть $\Pi_{\calL_0}=\ket0\bra0$ , а $\Pi_{\calL_1}=\ket1\bra1$ . Тогда

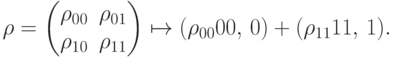
$\rho= \begin{pmatrix} \rho_{00}&\rho_{01}\\ \rho_{10}&\rho_{11} \end{pmatrix} \mapsto (\rho_{00}\ket0\bra0,\,0)+(\rho_{11}\ket1\bra1,\,1).$

Задача 10.6. "Квантовая телепортация" (см. [21]). Пусть имеются три q-бита: первый из них находится в произвольном (заранее неизвестном) состоянии $\rho$ , второй и третий — в состоянии

$\ket{\xi_{0,0}}=\frac{1}{\sqrt{2}}\Bigl(\ket{0,0}\double+\ket{1,1}\Bigr).$

Произведем над первыми двумя q-битами измерение, соответствующее ортогональному разложению

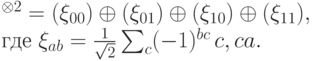
$\begin{multiple} \BB^{\otimes 2}&=\CC(\ket{\xi_{00}})\double\oplus\CC(\ket{\xi_{01}}) \double\oplus\CC(\ket{\xi_{10}})\double\oplus \CC(\ket{\xi_{11}}), \\ \mbox{где}\ \ket{\xi_{ab}}&= \frac{1}{\sqrt{2}} \sum_{c}(-1)^{bc}\,\ket{c,c\xor a}. \end{multiple}$

Покажите, что используя результат измерения и оставшийся третий q-бит, можно восстановить исходное состояние $\rho$ . Запишите всю последовательность действий (измерение и восстановление) в виде квантовой схемы.

Замечание 10.3. Этот процесс можно представлять таким образом. Допустим, что Алиса хочет передать Бобу^{1Эти два персонажа встречаются практически в любой статье по квантовой теории информации.} квантовое состояние $\rho$ по классическому каналу связи (например, по телефону). Оказывается, что это возможно, если Алиса и Боб заранее приготовили состояние $\ket{\xi_{00}}$ и взяли от него по половинке — одному q-биту. Алиса производит измерение и сообщает результат Бобу. Затем Боб переводит свой q-бит в состояние $\rho$ .

Дальше >>

Классические и квантовые вычисления

Классические и квантовые вычисления

Физически реализуемые преобразования матриц плотности

Измерение

Вопросы и ответы

Студенты

Авторизоваться

Классические и квантовые вычисления

Классические и квантовые вычисления

Физически реализуемые преобразования матриц плотности

Измерение

Вопросы и ответы

Студенты