| Россия |
Рекурсия и деревья
Вставка, поиск, удаление
Приведем рекурсивную функцию поиска в бинарном дереве поиска (эта и следующая функция добавлены в класс, реализующий бинарные деревья поиска):
has (x: G): BOOLEAN
— Есть ли x в каком-либо узле?
require
argument_exists: x /= Void
do
if x ~ item then
Result := True
elseif x < item then
Result := (left /=Void) and then left.has (x)
else — x > item
Result := (right /= Void) and then right.has (x)
end
end
Алгоритм имеет сложность O(h), где h – высота дерева, что означает O(log n) для полного или почти полного дерева.
В этом варианте приводится простая нерекурсивная версия алгоритма:
has1 (x: G): BOOLEAN
— Есть ли x в каком-либо узле?
require
argument_exists: x /= Void
local
node: BINARY_TREE [G]
do
from
node := Current
until
Result or node = Void
invariant
— x не находится в вышерасположенных узлах на нисходящем пути от корня
loop
if x < item then
node := left
elseif x > item then
node := right
else
Result := True
end
variant
— (Высота дерева) – (Длина пути от корня к узлу)
end
end
Для вставки элемента можно использовать следующую рекурсивную процедуру:
put (x: G)
— Вставка x, если он не присутствует в дереве.
require
argument_exists: x /= Void
do
if x < item then
if left = Void then
add_left (x)
else
left.put (x)
end
elseif x > item then
if right = Void then
add_right (x)
else
right.put (x)
end
end
end
Отсутствие ветви else во внешнем if отражает наше решение не размещать дублирующую информацию. Как следствие, вызов put с уже присутствующим значением не имеет эффекта. Это корректное поведение ("не жучок, а свойство"), о чем и уведомляет заголовочный комментарий. Некоторые пользователи могут, однако, предпочитать другой API с предусловием, устанавливающим not has(x).
Нерекурсивная версия остается в качестве упражнения.
Возникает естественный вопрос: как написать процедуру удаления – remove(x:G)? Это не так просто, поскольку нельзя просто удалить узел, содержащий x, если только это не лист дерева. Удаление листа сводится к обнулению одной из ссылок – left или right. Удаление произвольного узла приводило бы к нарушению инварианта бинарного дерева поиска.
Что следует сделать, так это реорганизовать дерево, перемещая узлы, лежащие в основании узла с найденным значением x, так, чтобы сохранить истинность инварианта.
В удаляемый узел нужно поместить элемент дерева, лежащий ниже удаляемого элемента. Есть два кандидата на эту роль, позволяющие сохранить истинность инварианта:
- в левом поддереве – это элемент с максимальным значением (такой элемент является листом дерева или имеет только одну связь);
- в правом поддереве – это элемент с минимальным значением.
Если перемещаемый элемент является листом дерева, то после перемещения соответствующий узел удаляется. Если элемент имеет одну ссылку, то ссылка родителя перемещаемого элемента связывается с потомком перемещаемого элемента, тем самым перемещаемый узел исключается из дерева. Инвариант при этих операциях сохраняется.
Предположим, что удаляется корень дерева – remove (35). Тогда в корень можно поместить либо элемент 23 (из левого поддерева), либо элемент 41 из правого поддерева.
Подобно поиску и вставке процесс удаления должен выполняться за время O(h), где h – это высота дерева. Процедура удаления остается в качестве упражнения.
Время программирования!
Напишите процедуру remove(x:G), которая удаляет элемент x, если он присутствует в дереве, сохраняя инвариант.
8.5. Перебор с возвратами и альфа-бета
Прежде чем исследовать теоретические основы рекурсивного программирования, полезно познакомиться еще с одним приложением, а точнее – с целым классом приложений, для которого рекурсия является естественным инструментом: алгоритмами перебора с возвратом. В имени отражена основная идея алгоритма: отыскивается решение некоторой проблемы, последовательно перебираются возможные пути; всякий раз, когда решение на данном пути заходит в тупик, происходит возврат назад к предыдущей развилке, из которой не все возможные пути были исследованы. Процесс заканчивается успешно, если на одном из путей достигается решение задачи. Неуспех в решении возникает тогда, когда ни на одном пути решение не получено или достигнут лимит времени, отведенный на поиск решения.
Перебор с возвратами применим к задаче, если каждое ее потенциальное решение может рассматриваться как последовательность выборов.
Бедственное положение застенчивого туриста
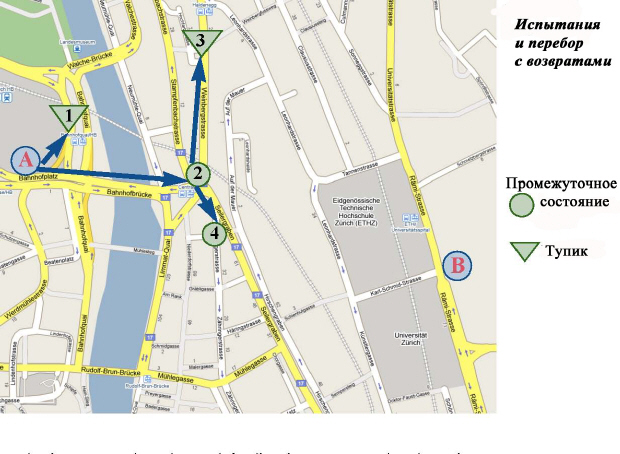
При необходимости достижения некоторой цели путешествия в незнакомом городе как к последней надежде можно прибегнуть к перебору с возвратом. Скажем, Вы находитесь в точке А (главная станция Цюриха) и хотите добраться до точки В (между главными зданиями ЕТН и Университета Цюриха):
Не имея карты и по застенчивости не отваживаясь спросить дорогу к цели, вы решили исследовать прилежащие улицы и проверять после каждой попытки, не достигнута ли цель (предполагается, что у вас есть фотография конечной точки). Вы знаете, что цель расположена на востоке, так что во избежание зацикливания все западно-ориентированные сегменты игнорируются.
На каждом этапе вы проверяете отрезки улиц, начиная с севера и двигаясь по часовой стрелке. Первая попытка приводит в точку 1. Здесь вы понимаете, что это не отвечает вашей цели, так как далее все возможные пути ведут на запад, то есть это тупик и нужно возвращаться назад в исходную точку А. Далее вы испытываете следующий выбор, приводящий в 2. Здесь есть несколько возможностей, и вначале вы проверяете путь, ведущий в 3, который оказывается тупиком, так что приходится вернуться в точку 2.
Если все "правильные" (не ведущие на запад) пути в 2 были исследованы и приводили к тупикам, то из 2 пришлось бы вернуться в точку А. Но в данной ситуации из 2 есть еще не исследованный выбор, ведущий в точку 4.
Процесс продолжается аналогичным образом, вы можете дополнить его самостоятельно, используя приведенную карту. Возможно, это не лучшая стратегия для путешествия в незнакомом городе, но иногда она может быть единственно возможной. Более важно, что она представляет общую схему метода "проб и ошибок", характерную для программирования перебора с возвратами. Схема может быть описана с помощью рекурсивной процедуры:
find ( p: PAT H): PATH
— Решение, если оно существует, начинающееся в P.
require
meaningful: p /= Void
local
c: LIST [CHOICE]
do
if p.is_solution then
Result := p
else
c := p.choices
from c.start until
(Result /= Void) or c.after
loop
Result := find ( p + c)
c.forth
end
end
end
Здесь применяются следующие соглашения. Выборы на каждом шаге описываются типом CHOICE (во многих ситуациях для этой цели можно использовать тип INTEGER). Есть также тип PATH, но каждый путь path – это просто последовательность выборов, и p + c – это путь, полученный присоединением c к p. Мы идентифицируем решение с путем, приводящим к цели, так что find возвращает PATH. По соглашению, если find не находит решения, то возвращается void. Запрос is_solution позволяет выяснить, найдено ли решение. Список выборов – p.choices, доступных из p, является пустым списком, если p – это тупик.
Для получения решения достаточно использовать find(p0), где p0 – начальный пустой путь.
Как обычно, Result инициализируется значением Void. Если в вызове find(p) ни один из рекурсивных вызовов на возможных расширениях p + c не вырабатывает решения (в частности, если таких расширений вообще нет, поскольку p.choices пусто), то цикл завершится со значением c.after, и тогда find(p) вернет значение Void. Если это был начальный вызов find(p0), то процесс завершается, не достигнув положительного результата, в противном случае рекурсивно включается следующий вызов, пока не будет получен результат или не будут перебраны все возможности.
Если один из вызовов находит, что p является решением, то p возвращается в качестве результата, и, подымаясь вверх по цепочке вызовов, результат возвращается, поскольку Result /= Void является условием выхода.
Рекурсия дает четкую основу для управления такой схемой. Это естественный способ выразить природу метода проб и ошибок в алгоритмах перебора с возвратом – техническая реализация рекурсии заботится обо всех деталях. Для осознания этого вклада представьте на секунду, как пришлось бы программировать эту схему без рекурсии, – понадобилось бы сохранять всю предысторию пройденных путей (я не предполагаю, что вам необходимо написать полную не рекурсивную версию, по крайней мере, на данном этапе, когда еще не изучены способы реализации рекурсии, излагаемые позже в данной лекции).
Правильная организация перебора с возвратом
Общая схема перебора с возвратом требует некоторой настройки для практического использования. Прежде всего, в том виде, как она приведена, не гарантируется завершаемость. Чтобы убедиться в завершаемости любого выполнения, необходимо одно из двух:
- иметь гарантию (приходящую от проблемной области), что нет бесконечных путей, другими словами, что при расширении любого пути настанет момент, когда появится пустой список выборов;
- определить длину максимального пути и адаптировать алгоритм так, чтобы достижение границы рассматривалось как тупик. Вместо длины пути можно аналогично вводить ограничение по времени. Любой вариант реализуется простыми изменениями предыдущего алгоритма.
Дополнительно практическая реализация обычно может обнаруживать эквивалентность некоторых путей, например, для ситуации, представленной на рисунке:
Пути [1, 2, 3, 4], [1, 2, 3, 4, 2, 3, 4], [1, 2, 3, 4, 2, 3, 4, 2, 3, 4] и так далее являются эквивалентными. Пример, демонстрирующий нахождение маршрута без циклов, состоял в важной рекомендации – "никогда не уезжайте на запад, молодой человек". Конечно, этот совет не может служить общей рекомендацией и связан лишь с конкретной проблемной ситуацией. Чтобы справиться с циклом, необходимо сохранять информацию о ранее посещенных точках и игнорировать любой путь, ведущий к такой точке.
Перебор с возвратами и деревья
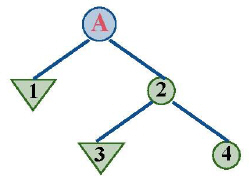
Для любой задачи, в решении которой может помочь перебор с возвратами, может помочь и построение модели в виде дерева. При установке соответствия будем использовать деревья, где каждый узел будет иметь произвольное число потомков, обобщая концепции, рассмотренные при определении бинарных деревьев. Путь в дереве (последовательность узлов) соответствует пути в алгоритме перебора (последовательность выборов). Дерево в примере с маршрутами представлено на рис. 8.21.
Мы можем представлять всю карту города подобным образом: узлы отражают местоположение указанных на карте точек, дуги представляют отрезки улиц, соединяющих точки. В результате получается граф. Граф может быть деревом только в том случае, если в нем нет циклов. Если граф не является деревом, то на его основе можно построить дерево, называемое остовным деревом графа, которое содержит все узлы графа и некоторые из его дуг. Для этого используются методы, упомянутые ранее, а также существует соглашение, позволяющее избежать цикла (никогда не ходите на запад) или построения путей из корня и исключающее любую дугу, которая ведет к ранее встречающемуся узлу. Вышеприведенное дерево является остовным деревом для части нашего примера, включающего узлы А, 1, 2, 3 и 4.
Для такого представления нашей задачи в виде дерева:
- решением является узел, удовлетворяющий заданному критерию (свойство, ранее названное is_solution, адаптированное для применения к узлам);
- выполнение алгоритма сводится к префиксному обходу дерева (самый левый в глубину).
В нашем примере этот порядок приведет к посещению узлов А, 1, 2, 3, 4.
Это соответствие указывает, что "Префиксный обход" и "Перебор с возвратами" основаны на одной и той же идее: всякий раз, когда мы рассматриваем возможный путь, мы разматываем все его возможные продолжения – все поддеревья узла, – прежде чем обращаемся к любому альтернативному выбору на уровне, представляющем непосредственных потомков узла. Например, если А на предыдущем рисунке будет иметь третьего потомка, то обход не будет его рассматривать, прежде чем не обойдет все поддеревья 2.
Единственное свойство, отличающее алгоритм перебора с возвратами от префиксного обхода, состоит в том, что он останавливается сразу же, как только найден узел, удовлетворяющий выбранному критерию.
Префиксный порядок был определен для бинарных деревьев следующим образом: посетить корень, затем обойти левое поддерево, затем правое. Порядок слева направо обобщается на произвольные деревья в предположении, что дети каждого узла упорядочены, – это не играет здесь существенной роли. Точно так же можно считать, что выборы для алгоритма перебора на каждом шаге упорядочены и просматриваются в соответствии с заданным порядком.