| Россия |
Рекурсия и деревья
Смеющаяся корова, изображенная на фирменном жетоне "Смеющаяся Корова", носит в качестве сережек фирменные жетоны, на которых, я подозреваю, но зрение не позволяет убедиться в правильности моего предположения, изображена корова с фирменными жетонами, на которых изображена … (надеюсь, идея понятна)1У нас известен рекурсивный стишок, вошедший в поговорку: "У попа была собака, он ее любил. Она съела кусок мяса, он ее убил, и в землю закопал, и на могиле написал, что у попа была собака …" .
Эта реклама, появившаяся в 1921 году, все еще хорошо работает, являясь примером структуры, определенной рекурсивно в следующем смысле:
Рекурсивное определение
"Рекурсия" – использование рекурсивного определения – широко применяется в программировании: она позволяет элегантно определять синтаксические структуры; мы также познакомимся с рекурсивно определенными структурами данных и рекурсивными процедурами.
Мы будем использовать термин "рекурсивный" как сокращение "рекурсивно определенный" – рекурсивная грамматика, рекурсивная структура данных. Но это только соглашение, поскольку нельзя сказать, что понятие или структура сами по себе рекурсивны. Все, что мы знаем, – это то, что их можно рекурсивно описать в соответствии с вышеприведенным определением. Любое частичное понятие – в том числе структура, задающая Смеющуюся корову, – может быть определено как рекурсивно, так и без использования рекурсии.
При рассмотрении свойств рекурсивно определенного понятия будем применять рекурсивные доказательства – обобщающие индуктивные доказательства, использующие целые числа для индуктивного шага.
Рекурсия является прямой, если определение  ссылается на экземпляр
ссылается на экземпляр  , и косвенной, если для
, и косвенной, если для 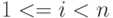 (для некоторого
(для некоторого  ) определение каждого
) определение каждого  ссылается на
ссылается на 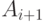 , а определение
, а определение 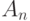 ссылается на
ссылается на 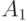 .
.
В этой лекции нас будут интересовать такие понятия, для которых рекурсивные определения естественны, элегантны и удобны. Примеры будут включать рекурсивные программы, рекурсивные синтаксические определения, рекурсивные структуры данных. Мы также получим некоторое представление о рекурсивных доказательствах.
Один из классов рекурсивных структур данных – деревья в их различных представлениях – появляются во многих приложениях и отражают очень точно идею рекурсии. В этой лекции рассматривается важный случай бинарных деревьев.
8.1. Основные примеры
В этот момент могут возникнуть вполне обоснованные сомнения – а есть ли смысл в рекурсивных определениях, как можно определить понятие через само понятие, "масло масляное"?
Вы вправе сомневаться. Не все рекурсивные определения хороши для определения чего-либо. Когда вас просят дать характеристику кому-нибудь, а вы отвечаете: "Света? Ну, это просто Света, что еще можно сказать!" – то вы не много нового сказали. Так что следует позаботиться о критериях, гарантирующих полезность определения, даже если оно рекурсивно.
Прежде чем мы это сделаем, позвольте убедиться прагматичным путем, ознакомившись с несколькими типичными примерами, когда рекурсия очевидно полезна и осмысленна. Это придаст нам твердую убежденность, большую, чем просто вера, основанная на надеждах и молитвах, что рекурсия – это практически полезный способ определять грамматики, структуры данных и алгоритмы. После чего настанет время для подходящего математического обоснования рекурсивных определений.
Рекурсивные определения
С введением универсальности мы получаем возможность определять тип как:
| Т1 | класс, не являющийся универсальным, такой как INTEGER или STATION; |
| Т2 | родовое порождение в форме C[T], где С – универсальный класс, а Т – тип. |
Это определение рекурсивно, оно просто означает, что, при наличии универсальных классов ARRAY и LIST, правильными классами также будут:
- INTEGER, STATION и им подобные в соответствии с определением Т1;
- согласно случаю Т2, прямые родовые порождения: ARRAY[INTEGER], LIST[STATION] и так далее.
Используя подобный прием, можно дать ответ на упражнение из первой лекции, где требовалось дать определение алфавитному (лексикографическому) порядку.
Рекурсивно определенные грамматики
Рассмотрим подмножество Eiffel с двумя видами операторов.
- Присваивание, в его обычной форме variable:= expression, рассматриваемое здесь как терминальное и далее не уточняемое.
- Условный оператор, имеющий только часть then (без else) для простоты.
Грамматика, определяющая язык, такова:

Для наших непосредственных целей будем полагать, что "Условие" является терминальным понятием. Это определение грамматики очевидно рекурсивно, поскольку определение "Оператор" включает "Условный", а его определение, в свою очередь, включает "Оператор". Но так как здесь присутствует нерекурсивная часть определения – "Присваивание", то в целом грамматика четко определяет правильные конструкции языка:
- просто Присваивание;
- Условный, содержащий Присваивание: if c then a end;
- то же самое с произвольной степенью вложенности: if c1 then if c2 then a end end, if c1 then if c2 then if c3 then a end end end и так далее.
Рекурсивные грамматики на самом деле являются незаменимым средством для описания любого языка, который, как все распространенные языки, поддерживает вложенные структуры.
Рекурсивно определенные структуры данных
Класс STOP представляет понятие остановки для линии метро:
class STOP create
…
feature
next: STOP
— Следующая остановка на той же линии.
…Другие компоненты, здесь опущенные (см.6.5)
end
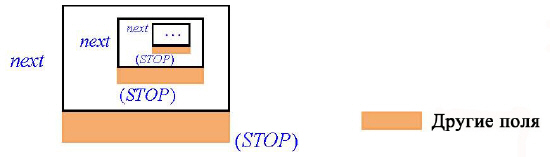
Наивная интерпретация будет предполагать, что каждый экземпляр STOP содержит экземпляр STOP, который, в свою очередь, содержит остановку и так до бесконечности, как в схеме со Смеющейся коровой. Это и в самом деле было бы так, если бы STOP принадлежал развернутым, а не ссылочным типам:
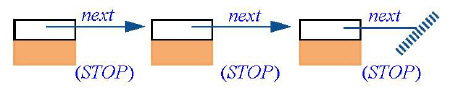
Такое попросту невозможно. Но STOP в любом случае является ссылочным типом, подобно любому классу, определенному как class X… без всяких других квалификаций, так что реальная картина выглядит так:
Рекурсия в таком определении структуры данных просто указывает, что каждый экземпляр класса потенциально содержит ссылку на экземпляр того же класса, "потенциально" – поскольку ссылка может иметь значение void, и тогда действие рекурсии прекращается, как для последней остановки на рисунке.
В той же 6-й главе, где рассматривались линии метро, шла речь и о классе PERSON c атрибутом spouse типа PERSON.
Это весьма общая ситуация в определении полезных структур данных, начиная от связных списков до деревьев различного вида (таких как бинарные деревья, изучаемые позже в этой лекции). Определения полезных классов часто включают ссылки на объекты определяемого класса или (косвенная рекурсия) на классы, зависящие от определяемого.
Рекурсивно определяемые алгоритмы и программы
Известная последовательность чисел Фибоначчи обладает многими прекрасными свойствами и появляется во многих приложениях математики и естественных наук. Она имеет следующее определение:
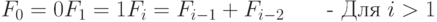
Почувствуй историю
Леонардо Фибоначчи из Пизы (1170 – 1250) сыграл ключевую роль в знакомстве Запада с трудами индийских и арабских математиков. Он известен также и собственными исследованиями, лежащими в основании современной математики. Он сформулировал задачу, приводящую к его знаменитой последовательности (которая была известна еще индийским математикам):
Человек получил пару кроликов и поместил их в загон, окруженный со всех сторон стеной. Как много пар кроликов можно получить от этой пары в год, если каждый месяц каждая пара производит новую пару, которая становится продуктивной на втором месяце?
Решение дает следующее рассуждение. Пары кроликов в месяце  включают пары кроликов, уже существующие в предыдущем месяце (кролики не умирают); обозначим их число как
включают пары кроликов, уже существующие в предыдущем месяце (кролики не умирают); обозначим их число как 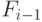 , плюс потомство, принесенное кроликами, жившими в месяце
, плюс потомство, принесенное кроликами, жившими в месяце 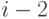 (кролики, появившиеся в месяце
(кролики, появившиеся в месяце 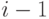 , потомства не приносят). Это и дает приведенную выше формулу, создающую последовательность целых чисел 0, 1, 1, 2, 3, 5, 8 и так далее. Формула приводит к рекурсивной программе, вычисляющей
, потомства не приносят). Это и дает приведенную выше формулу, создающую последовательность целых чисел 0, 1, 1, 2, 3, 5, 8 и так далее. Формула приводит к рекурсивной программе, вычисляющей 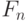 для любого
для любого  :
:
fibonacci (n: INTEGER): INTEGER
— Элемент с индексом n в последовательности Фибоначчи.
require
non_negative: n >= 0
do
if n = 0 then
Result := 0
elseif n = 1 then
Result := 1
else
Result := fibonacci(n – 1)+ fibonacci(n – 2)
end
end
Время программирования!
Напишите небольшую программную систему, включающую вышеприведенную рекурсивную функцию и печатающую ее результат. Протестируйте ее для небольших значений n, включая 12, как в оригинальном тексте Фибоначчи.
Функция включает два рекурсивных вызова. То, что это работает, может казаться несколько загадочным (вот почему стоит проверить выполнение функции на нескольких значениях). После изучения этой лекции легитимность таких рекурсивно определенных программ должна стать вполне понятной.
Принципиальным аргументом в пользу такого способа записи программы есть то, что она вполне соответствует математическому определению последовательности Фибоначчи. Дальнейшее рассмотрение покажет, что этот факт не столь впечатляющий, поскольку получить нерекурсивную версию также не сложно.
Время программирования!
Можете ли вы, не заглядывая в дальнейший текст, написать функцию, вычисляющую N-е число Фибоначчи, используя цикл, а не рекурсию?
Следующая функция дает тот же результат, что и рекурсивная версия. Проверьте это на нескольких значениях.
fibonacci1 (n: INTEGER): INTEGER
— Элемент с индексом n в последовательности Фибоначчи.
— (Нерекурсивная версия.)
require
positive: n >=1
local
i, previous, second_previous: INTEGER
do
from
i := 1 ; Result := 1
invariant
Result = fibonacci(i )
previous = fibonacci (i – 1)
until i = n loop
i := i + 1
second_previous := previous
previous := Result
Result := previous + second_previous
variant
n – i
end
end
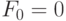 . Переменная second_previous обновляется на каждом шаге цикла и ей не нужно специальной инициализации.
. Переменная second_previous обновляется на каждом шаге цикла и ей не нужно специальной инициализации.Эта версия более удалена от оригинального математического определения, но все же проста и понятна. Заметьте: инвариант цикла ссылается для удобства на рекурсивную функцию, представляющую официальное математическое определение. Некоторые могут предпочитать рекурсивную версию в любом случае, но это дело вкуса. В зависимости от компилятора рекурсивная версия может быть менее эффективной по времени выполнения.
Оставим в стороне вкус и эффективность. Если бы мы рассматривали только такие примеры, то необходимость рекурсивных программ была бы далеко не очевидной. Нам необходимы примеры, в которых рекурсия обеспечила бесспорные преимущества, например, за счет того, что ее нерекурсивный аналог был бы значительно сложнее и труднее в понимании. Такие примеры существуют в большом количестве. Одним из них является очаровательная головоломка – "Ханойская башня". В этом примере сконцентрировано много полезных свойств рекурсии, и практически нет не относящихся к делу деталей.