| Россия |
Эквивалентность и порядок. Изоморфизмы
Изоморфизмы
Два частично упорядоченных множества называются изоморфными, если между ними существует изоморфизм, то есть взаимно однозначное соответствие,
сохраняющее порядок. (Естественно, что в этом случае
они равномощны как множества.) Можно сказать так:
биекция 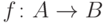 называется изоморфизмом частично
упорядоченных множеств
называется изоморфизмом частично
упорядоченных множеств  и
и  , если
, если
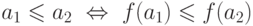
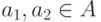 (слева знак
(слева знак 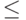 обозначает
порядок в множестве
обозначает
порядок в множестве  , справа - в множестве
, справа - в множестве  ).
).Очевидно, что отношение изоморфности рефлексивно (каждое множество
изоморфно самому себе), симметрично (если  изоморфно
изоморфно  , то
и наоборот) и транзитивно (два множества, изоморфные третьему,
изоморфны между собой). Таким образом, все частично
упорядоченные множества разбиваются на классы изоморфных,
которые называют порядковыми типами.
(Правда, как и с
мощностями, тут необходима осторожность - изоморфных множеств
слишком много, и потому говорить о порядковых типах как
множествах нельзя.)
, то
и наоборот) и транзитивно (два множества, изоморфные третьему,
изоморфны между собой). Таким образом, все частично
упорядоченные множества разбиваются на классы изоморфных,
которые называют порядковыми типами.
(Правда, как и с
мощностями, тут необходима осторожность - изоморфных множеств
слишком много, и потому говорить о порядковых типах как
множествах нельзя.)
Теорема 12. Конечные линейно упорядоченные множества из одинакового числа элементов изоморфны.
Доказательство.
Конечное линейно упорядоченное множество всегда имеет наименьший
элемент (возьмем любой элемент; если он не наименьший, возьмем меньший,
если и он не наименьший, еще меньший - и так далее; получим
убывающую последовательность  , которая рано
или
поздно должна оборваться). Присвоим наименьшему элементу номер
, которая рано
или
поздно должна оборваться). Присвоим наименьшему элементу номер  .
Из оставшихся снова выберем наименьший
элемент и присвоим ему номер
.
Из оставшихся снова выберем наименьший
элемент и присвоим ему номер  и так далее. Легко понять,
что порядок между элементами соответствует порядку между
номерами, то есть что наше множество изоморфно множеству
и так далее. Легко понять,
что порядок между элементами соответствует порядку между
номерами, то есть что наше множество изоморфно множеству 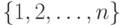 .
.
95. Докажите, что множество всех целых положительных делителей
числа  с отношением " быть делителем" в качестве
отношения порядка изоморфно множеству всех подмножеств
множества
с отношением " быть делителем" в качестве
отношения порядка изоморфно множеству всех подмножеств
множества 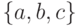 , упорядоченному по включению.
, упорядоченному по включению.
96. Будем рассматривать финитные последовательности натуральных
чисел, то есть последовательности, у которых все члены, кроме
конечного числа, равны  . На множестве таких
последовательностей введем покомпонентный порядок:
. На множестве таких
последовательностей введем покомпонентный порядок: 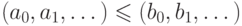 , если
, если  при всех
при всех  . Докажите, что это множество изоморфно множеству
всех положительных целых чисел с отношением " быть
делителем" в качестве порядка.
. Докажите, что это множество изоморфно множеству
всех положительных целых чисел с отношением " быть
делителем" в качестве порядка.
Взаимно однозначное отображение частично упорядоченного
множества  в себя, являющееся изоморфизмом,
называют автоморфизмом частично
упорядоченного множества
в себя, являющееся изоморфизмом,
называют автоморфизмом частично
упорядоченного множества  .
Тождественное отображение всегда является автоморфизмом, но
для некоторых множеств существуют и другие автоморфизмы. Например,
отображение прибавления единицы (
.
Тождественное отображение всегда является автоморфизмом, но
для некоторых множеств существуют и другие автоморфизмы. Например,
отображение прибавления единицы ( 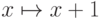 ) является
автоморфизмом частично упорядоченного множества
) является
автоморфизмом частично упорядоченного множества 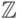 целых чисел (с естественным порядком). Для множества
натуральных чисел та же формула не дает автоморфизма
(нет взаимной однозначности).
целых чисел (с естественным порядком). Для множества
натуральных чисел та же формула не дает автоморфизма
(нет взаимной однозначности).
97. Покажите, что не существует автоморфизма упорядоченного
множества  натуральных чисел, отличного от тождественного.
натуральных чисел, отличного от тождественного.
98. Рассмотрим множество 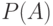 всех подмножеств некоторого
всех подмножеств некоторого  - элементного множества
- элементного множества  , частично упорядоченное
по включению. Найдите число автоморфизмов этого множества.
, частично упорядоченное
по включению. Найдите число автоморфизмов этого множества.
99. Покажите, что множество целых положительных чисел, частично
упорядоченное отношением "  делит
делит  ", имеет
континуум
различных автоморфизмов.
", имеет
континуум
различных автоморфизмов.
Вот несколько примеров равномощных, но не изоморфных линейно упорядоченных множеств (в силу теоремы 12 они должны быть бесконечными).
- Отрезок
![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) (с обычным отношением порядка)
не изоморфен множеству
(с обычным отношением порядка)
не изоморфен множеству  , так как у первого
есть наибольший элемент, а у второго нет. (При изоморфизме
наибольший элемент, естественно, должен соответствовать
наибольшему.)
, так как у первого
есть наибольший элемент, а у второго нет. (При изоморфизме
наибольший элемент, естественно, должен соответствовать
наибольшему.) - Множество
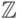 (целые числа с обычным порядком)
не изоморфно множеству
(целые числа с обычным порядком)
не изоморфно множеству  (рациональные числа).
В самом деле, пусть
(рациональные числа).
В самом деле, пусть  является
изоморфизмом.
Возьмем два соседних целых
числа, скажем,
является
изоморфизмом.
Возьмем два соседних целых
числа, скажем,  и
и  .
При изоморфизме
.
При изоморфизме  им должны соответствовать какие - то два
рациональных числа
им должны соответствовать какие - то два
рациональных числа  и
и 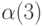 , причем
, причем 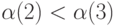 , так как
, так как  . Но тогда
рациональным
числам между
. Но тогда
рациональным
числам между  и
и 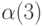 должны
соответствовать
целые числа между
должны
соответствовать
целые числа между  и
и  , которых
нет.
, которых
нет. - Более сложный пример - множества
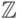 и
и  .
Возьмем в
.
Возьмем в  две
копии нуля (из той и другой компоненты); мы обозначали их
две
копии нуля (из той и другой компоненты); мы обозначали их  и
и  .
При этом
.
При этом  . При изоморфизме им должны
соответствовать два целых числа
. При изоморфизме им должны
соответствовать два целых числа  и
и  , для
которых
, для
которых 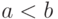 . Тогда всем элементам между
. Тогда всем элементам между  и
и  (их бесконечно
много:
(их бесконечно
много:  ,
,  ,
,  ,
,  ,
, 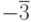 ,
, 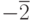 ,
, 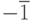 )
должны соответствовать числа между
)
должны соответствовать числа между  и
и  - но их
лишь конечное
число.
- но их
лишь конечное
число.Этот пример принципиально отличается от предыдущих тем, что здесь разницу между свойствами множеств нельзя записать формулой. Как говорят, упорядоченные множества
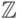 и
и  " элементарно эквивалентны".
" элементарно эквивалентны".
