| Россия |
Теорема Кантора - Бернштейна
Определение равномощности уточняет интуитивную идею о множествах " одинакового размера". А как формально определить, когда одно множество " больше" другого?
Говорят, что множество  по мощности не больше
множества
по мощности не больше
множества  , если оно равномощно некоторому подмножеству
множества
, если оно равномощно некоторому подмножеству
множества  (возможно, самому
(возможно, самому  ).
).
44. Некто предложил такое определение: множество  имеет строго
меньшую мощность, чем множество
имеет строго
меньшую мощность, чем множество  , если оно равномощно
некоторой части множества
, если оно равномощно
некоторой части множества  , не совпадающей со
всем
, не совпадающей со
всем  .
Почему это определение неудачно?
(Указание. Популярные рассказы о теории множеств часто начинаются с такого
парадокса, восходящего к Галилею.
Каких чисел больше - всех натуральных чисел или точных квадратов? С одной
стороны, точные квадраты составляют лишь небольшую часть
натуральных чисел; с другой стороны их можно поставить во
взаимно однозначное соответствие со всеми натуральными числами.)
.
Почему это определение неудачно?
(Указание. Популярные рассказы о теории множеств часто начинаются с такого
парадокса, восходящего к Галилею.
Каких чисел больше - всех натуральных чисел или точных квадратов? С одной
стороны, точные квадраты составляют лишь небольшую часть
натуральных чисел; с другой стороны их можно поставить во
взаимно однозначное соответствие со всеми натуральными числами.)
Отношение " иметь не большую мощность" обладает многими естественными свойствами:
- Если
 и
и  равномощны, то
равномощны, то  имеет
не большую мощность,
чем
имеет
не большую мощность,
чем  . (Очевидно.)
. (Очевидно.) - Если
 имеет не большую мощность, чем
имеет не большую мощность, чем  , а
, а  имеет не большую
мощность, чем
имеет не большую
мощность, чем  , то
, то  имеет не большую мощность,
чем
имеет не большую мощность,
чем  .
(Тоже несложно. Пусть
.
(Тоже несложно. Пусть  находится во взаимно однозначном
соответствии с
находится во взаимно однозначном
соответствии с 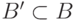 , а
, а  находится во
взаимно однозначном
соответствии с
находится во
взаимно однозначном
соответствии с 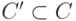 . Тогда при втором соответствии
. Тогда при втором соответствии 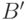 соответствует некоторому множеству
соответствует некоторому множеству 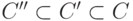 ,
как показано на рис.3.1, и потому
,
как показано на рис.3.1, и потому  равномощно
равномощно  .)
.)
- Если
 имеет не большую мощность, чем
имеет не большую мощность, чем  , а
, а  имеет не большую
мощность, чем
имеет не большую
мощность, чем  , то они равномощны. (Это вовсе не очевидное
утверждение составляет содержание теоремы Кантора - Бернштейна,
которую мы сейчас докажем.)
, то они равномощны. (Это вовсе не очевидное
утверждение составляет содержание теоремы Кантора - Бернштейна,
которую мы сейчас докажем.) - Для любых двух множеств
 и
и  верно (хотя бы)
одно из двух:
либо
верно (хотя бы)
одно из двух:
либо  имеет не большую мощность, чем
имеет не большую мощность, чем  , либо
, либо  имеет не
большую мощность, чем
имеет не
большую мощность, чем  . (Доказательство этого факта требует
так называемой " трансфинитной индукции" см.
"Теорема Цермело"
,
теорема 25.)
. (Доказательство этого факта требует
так называемой " трансфинитной индукции" см.
"Теорема Цермело"
,
теорема 25.)
Теорема 5. (Кантора-Бернштейна)
Если множество  равномощно некоторому подмножеству
множества
равномощно некоторому подмножеству
множества  , а
, а  равномощно некоторому подмножеству
множества
равномощно некоторому подмножеству
множества  , то множества
, то множества  и
и  равномощны.
равномощны.
Доказательство
Пусть  равномощно подмножеству
равномощно подмножеству 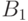 множества
множества  , а
, а  равномощно подмножеству
равномощно подмножеству 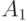 множества
множества  (см. рис. 3.2).
(см. рис. 3.2).
При
взаимно однозначном соответствии между  и
и 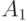 подмножество
подмножество 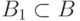 переходит в некоторое
подмножество
переходит в некоторое
подмножество  . При этом все три множества
. При этом все три множества  ,
, 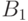 и
и 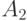 равномощны, - и нужно
доказать, что они
равномощны множеству
равномощны, - и нужно
доказать, что они
равномощны множеству  , или, что то же
самое,
, или, что то же
самое, 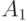 .
.
Теперь мы можем забыть про множество  и его подмножества
и доказывать такой факт:
и его подмножества
и доказывать такой факт:
если
и
равномощно
, то все три множества равномощны.
(Для единообразия мы говорим 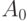 вместо
вместо  .)
.)
Пусть  - функция, осуществляющая взаимно однозначное
соответствие
- функция, осуществляющая взаимно однозначное
соответствие 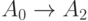 (элемент
(элемент 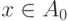 соответствует элементу
соответствует элементу  ). Когда
). Когда 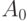 переходит
в
переходит
в 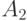 , меньшее множество
, меньшее множество 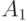 переходит в какое-то
множество
переходит в какое-то
множество  (см. рис. 3.3). Аналогичным
образом само
(см. рис. 3.3). Аналогичным
образом само 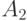 переходит в некоторое
множество
переходит в некоторое
множество  . При этом
. При этом  , так
как
, так
как  .
.