Упорядоченные бинарные диаграммы решений (УБДР)

Построение сокращенных УБДР по формулам

Алгоритм СОКРАЩЕНИЕ-УБДР позволяет построить сокращенную УБДР для функции f, по любой другой ее УБДР. Но как построить УБДР, если f задана, например, с помощью формулы? Можно, конечно, попытаться построить полное бинарное дерево решений, объединить в нем все листья с меткой 0 в один сток, а листья с меткой 1 - в другой. Затем применить к получившейся УБДР алгоритм СОКРАЩЕНИЕ-УБДР. Но этот подход годится только для функций от небольшого числа переменных, так как полное БДР для f(x₁, ..., x_n) будет содержать 2ⁿ листьев.

Другой подход связан с построением УБДР "сверху-вниз". Объясним его для естественного порядка переменных: x₁< x₂ < ... < x_n.

Начнем построение с корня, помеченного x₁. Рассмотрим две остаточные функции: f₀(x₁, ..., x_n)=f(0, x₂, ..., x_n) и f₁(x₂, ..., x_n)=f(1, x₂, ..., x_n). Если они одинаковы, то f не зависит от x₁ и тогда изменим метку у корня на x₂. Если обе функции f₀ и f₁ существенно зависят от x₂, то для каждой из них добавляем вершину, помеченную x₂, и далее реализуем по индукции. Если 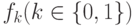не зависит от переменных x₂,... , x_j, но зависит существенно от x_j+1, то добавляем вершину, помеченную x_j+1, и проводим в нее ребро с меткой k из вершины, соответствующей f . Пусть для некоторого i уже построены вершины для всех различных остаточных функций вида 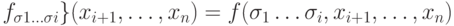, существенно зависящих от x_i. Для каждой из них получим две остаточные функци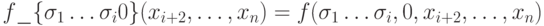и и 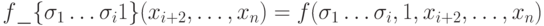. Затем выберем из множества этих функций разные, для каждой из них добавим в диаграмму вершину, помеченную x_i+1, и проведем в них соответствующие ребра из вершин, помеченных x_{i}. Продолжая построение, дойдем до функций от 1-ой переменной x_n и до констант, для которых минимальные реализации очевидны.

Пример 3.2. Рассмотрим, например, функцию f(x₁, x₂, x₃, x₄), заданную формулой 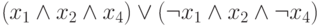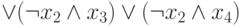, и построим для нее УБДР относительно порядка x₁ < x₂ < x₃ <x₄, используя описанную выше процедуру.

Вначале создадим корень, помеченный x₁, и рассмотрим остаточные функции, получающиеся при x₁=0 и x₁ =1. Имеем

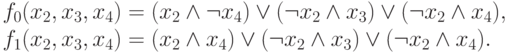
Они разные и обе существенно зависят от x₂. Поэтому добавим для каждой из них вершину, помеченную x₂. Затем для каждой из них определим остаточные функции, получающиеся при x₂=0 и x₂ =1. Получим

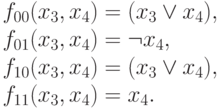
Так как f₀₀=f₁₀, а f₀₁ и f₁₁ от x₃ не зависят, то нам потребуется только одна вершина, помеченая x₃. Она будет представлять функцию . При x₃=0 она превращается в x₄, а при x₃=1 равна константе 1. В результате получается УБДР D_f, показанная на рис.3.6.

Рис. 3.6.

Задачи

Задача 3.1. Докажите, что совершенная, сокращенная и минимальная ДНФ функции odd(X₁,X₂,..., X_n) совпадают и состоят из 2_n-1 элементарных конъюнкций длины n.

Задача 3.2. Докажите лемму 3.2 возвратной индукцией по i.

Задача 3.3. Используя лемму 3.2, докажите утверждение 2 теоремы 3.2.

Задача 3.4. Постройте минимальные УБДР для двуместных функций: .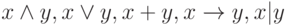

Задача 3.5. Постройте минимальные УБДР для функции

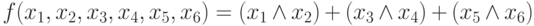
относительно двух упорядочений переменных:

• x₁ < x₂ < x₃ < x₄ < x₅ < x₆ и
• x₁ < x₃ < x₅ < x₂ < x₄ < x₆.

Задача 3.6. Пороговая функция T_n^k от n переменных с порогом k выдает 1, если во входном наборе имеется не менее k единиц: .

• Постройте минимальные УБДР для пороговых функций T₃², T₄², T₅³.
• Зависит ли сложность минимальной УБДР для пороговых функций от порядка переменных?
• Оцените сложность минимальной УБДР для пороговой функции T_n^k.

Задача 3.7. Выберите подходящий порядок переменных и постройте для него минимальные УБДР, реализующие функции из задач 12.5 и 12.6.

Задача 3.8. Как мы видели, логические схемы естественным образом реализуются в виде неветвящихся программ. Наоборот, для деревьев решений и УБДР естественным программным представлением являются ветвящиеся программы, включающие лишь условные операторы вида if ... then ... else ... с тестами вида "x = 0?" и "x = 1?" (они соответствуют внутренним вершинам диаграмм) и операторы присвоения значения 0 или 1 результату (они соответствуют вершинам- стокам ).

Напишите ветвящиеся программы, вычисляющие функции, представляемые УБДР D₂ на рис. 3.3 и D_f на рис.3.6.