Лекция 13: Решение задач нелинейного программирования с ограничениями. Геометрическая интерпретация задач нелинейного программирования

3. Метод барьерных поверхностей (метод Кэррола)

Если ограничения в задаче имеют вид чистых неравенств, т.е.

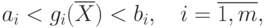
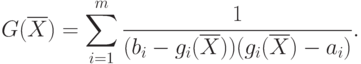
Как только одна из функций 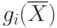достигнет своего предела ( a_i или b_i ), штраф 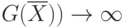, т.е. возникнет т.н. "барьер".

Метод был предложен Кэрролом, и получил название метода барьерных поверхностей (МБП) Кэррола.

При этом ограничения в виде равенств и неравенств всегда можно преобразовать в ограничения в виде чистых неравенств, если к величине ограничения добавить очень малое число (например, 10^-5 ).

Рассмотрим действие данного метода на примере задачи оптимального проектирования контейнера.

Пусть требуется спроектировать контейнер в форме прямоугольного параллелепипеда объемом V=1м³. Желательно, чтобы при изготовлении контейнеров затрачивалось как можно меньше материалов. Чтобы его было удобно брать автопогрузчиком, ширина должна быть не менее 1,5 м.

Строим математическую модель контейнера.

1) Формируем вектор переменных . Параметрами вектора переменных являются: длина x₁, ширина x₂ и высота x₃ контейнера, т.е.

( 3.1)

2) Строим целевую функцию . При условии постоянства толщины стенок контейнера требование минимизировать количество материала можно свести к минимизации площади боковой поверхности контейнера.

Тогда

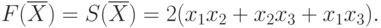( 3.2)

3) Формируем ограничения.

Ограничение-равенство:

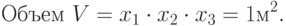( 3.3)

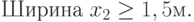( 3.4)

Упростим математическую модель контейнера. Ограничение – равенство (3.3) в задаче, благодаря своей простоте, позволяет уменьшить размерность задачи, т.е.

x3 = 1/x1x2 .

В результате параметр x₃ можно исключить из вектора проектных параметров, и из трехмерной задачи мы получим двумерную. Тогда вектор будет иметь вид:

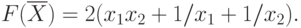
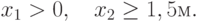
В результате, задача проектирования контейнера может быть сформулирована следующим образом:

Найти вектор , доставляющий минимум целевой функции

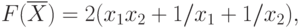
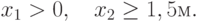
В данной задаче барьерная функция может иметь вид:

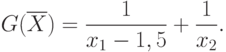
Как только один из параметров x₁ или x₂ достигнет своего предела, штраф 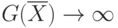, т.е. возникнет т.н. "барьер".

Штрафная функция в задаче проектирования контейнера будет иметь вид:

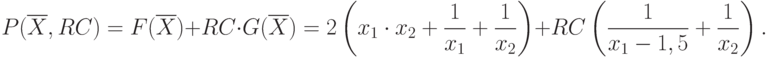
Для нахождения минимума этой штрафной функции (задача двумерная) может быть использован метод многомерной оптимизации.