|
В уравнениях движения кривошипно-шатунного механизма вместо обозначения радиуса кривошипа "r" ошибочно записан символ "?" (гамма). P.S. Может быть это слишком очевидно, но не упомянуто, что угол поворота кривошипа ? считается малым. |
Случайные события, случайные величины. Их законы распределения и числовые характеристики
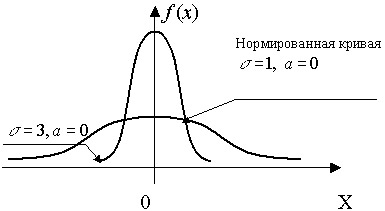
Изменение величины параметра  (среднего квадратичного отклонения) изменяет форму нормальной кривой: с возрастанием
(среднего квадратичного отклонения) изменяет форму нормальной кривой: с возрастанием  ординаты нормальной кривой убывают, кривая растягивается вдоль оси X и прижимается к ней. При убывании
ординаты нормальной кривой убывают, кривая растягивается вдоль оси X и прижимается к ней. При убывании  ординаты нормальной кривой увеличиваются, кривая сжимается вдоль оси X и становится более "островершинной".
ординаты нормальной кривой увеличиваются, кривая сжимается вдоль оси X и становится более "островершинной".
При этом, при любых значениях  и
и  площадь ограниченная нормальной кривой и осью X, остается равной единице (т. е. вероятность того, что случайная величина, распределенная нормально, примет значение ограниченное на оси X нормальной кривой, равна 1).
площадь ограниченная нормальной кривой и осью X, остается равной единице (т. е. вероятность того, что случайная величина, распределенная нормально, примет значение ограниченное на оси X нормальной кривой, равна 1).
Нормальное распределение с произвольными параметрами  и
и  т. е. описываемое дифференциальной функцией
т. е. описываемое дифференциальной функцией
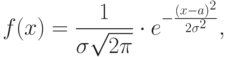
Нормальное распределение с параметрами 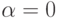 и
и  , т. е. описываемое дифференциальной функцией
, т. е. описываемое дифференциальной функцией
 |
( 6.6) |
называется нормированным распределением (рис. 6.8). В нормированном распределении дифференциальная функция распределения равна:
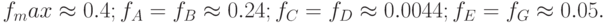
Интегральная функция общего нормального распределения имеет вид:
 |
( 6.7) |
Интегральная функция нормированного распределения имеет вид:
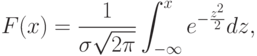 |
( 6.8) |
где
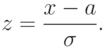
Пусть случайная величина X распределена по нормальному закону в интервале (c, d). Тогда вероятность того, что X примет значение, принадлежащее интервалу (c, d) равна
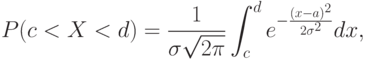
Пронормируем это выражение. Для этого введем новую переменную z
Откуда:  .
.
Новые пределы интегрирования:
Для 
для 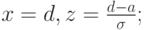
Тогда, после нормирования, вероятность того, что случайная величина X примет значение, принадлежащее интервалу (c, d) равна

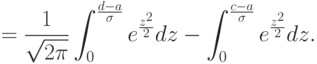
Пользуясь функцией Лапласа (функция табулирована)
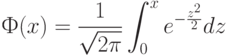
окончательно получим
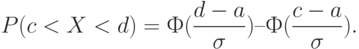
Пример.
Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратичное отклонение этой случайной величины равны a=30 и 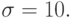 Найти вероятность того, что X примет значение в интервале (10, 50).
Найти вероятность того, что X примет значение в интервале (10, 50).
Решение:
Тогда

Пользуясь готовыми таблицами Лапласа, имеем:
Отсюда 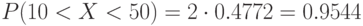 .
.

 .
.