Задача ГП с ограничениями

Связь между ГП и линейным программированием

Напомним постановку задачи линейного программирования.

Задача ЛП - это задача поиска экстремума (максимума или минимума) линейной функции многих переменных при наличии линейных ограничений (равенств или неравенств), связывающих эти переменные:

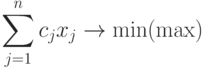
при ограничениях

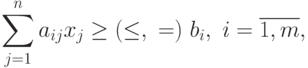
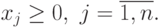
Одним из подходов к решению задач ГП является замена ее задачей линейного программирования, в которой целевая функция и функции ограничений являются линейными аппроксимациями соответствующих позиномов. Желающие могут прочесть об этом в статье [6]. Мы же рассмотрим на примере реализацию этого подхода для частного случая задач ГП, когда все позиномы являются мономами.

Пример 36 Найдем длины сторон параллелепипеда, имеющего наибольший объем, если площадь нижней и верхней стороны не превышает 20 (см 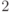), площадь фронтальных сторон не превышает 10 (см 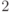), площадь боковых сторон не превышает 5 (см ).

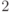Введем обозначения: - ширина параллелепипеда, - длина, 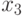- высота параллелепипеда. Тогда математическая модель задачи примет вид:

при ограничениях:

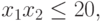
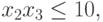
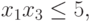
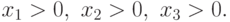
Эта задача эквивалентна следующей задаче ГП в каноническом виде:

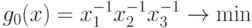
при ограничениях:

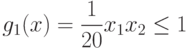
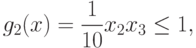
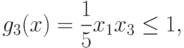
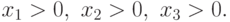
Все позиномы в задаче являются мономами. Сведем эту задачу ГП к задаче ЛП. Выполним следующую замену переменных: 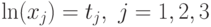. Получим эквивалентную задачу линейного программирования, в которой переменные могут иметь любой знак:

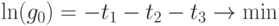
при ограничениях

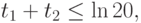
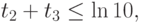
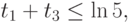
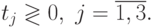
Сведем эту задачу к задаче ЛП в стандартном виде, выполнив замену:

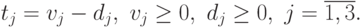
В результате получим следующую задачу ЛП:

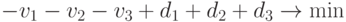
при ограничениях

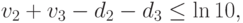
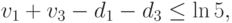
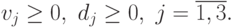
Для решения задач ЛП в этом курсе мы будем использовать пакет FinPlus, в котором реализован двухфазный модифицированный симплекс-метод. Версия пакета FinPlus для свободного копирования и руководство пользователя размещены на сайте exponenta.ru:

Рис. 5.1. FinPlus: ввод данных задачи

Рис. 5.2. FinPlus: лист с отчетом о решении задачи

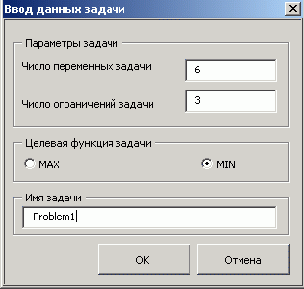
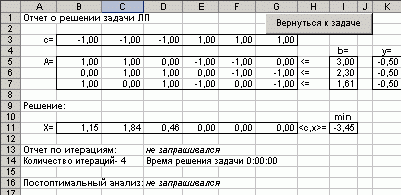
Решим задачу в пакете FinPlus. На рис. 5.1 показано диалоговое окно для ввода размерности задачи, типа целевой функции и имени задачи. На рис. 5.2 приведен фрагмент рабочего листа с данными задачи и ее решением:

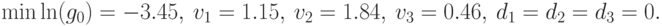
Выполнив обратную замену 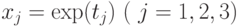, получим:

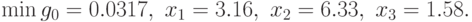
Таким образом, максимальный объем параллелепипеда, равный 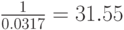(см 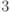), достигается при следующих размерах: ширина 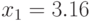(см), длина 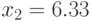(см), высота 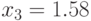(см).

Замечание. При такой постановке задачи ГП (когда все позиномы являются мономами) не обязательно приводить задачу ГП к каноническому виду.

О методах решения задач ГП с ограничениями

Методы решения задач ГП можно разделить на прямые, решающие прямую задачу ГП, и двойственные, решающие соответствующую двойственную задачу. Ряд авторов считают двойственные методы наиболее эффективными. Мы не будем излагать общие методы решения задач ГП в этом вводном курсе, так как они довольно сложны. Сообщим только, что на практике чаще всего используют метод внутренней точки ([7]) и метод Ражгопала-Бриккера ([9]). Последний метод основан на обобщенном линейном программировании и идее метода генерации столбцов.

Краткие итоги

Приведены постановки прямой задачи ГП с ограничениями в канонической форме и двойственной к ней задачи. Введено определение совместной задачи ГП. Сформулированы теоремы двойственности для задачи ГП с ограничениями. Описана связь между теорией выпуклого программирования и геометрическим программированием, а также связь между линейным и геометрическим программированием. Описано преобразование задачи ГП в выпуклую задачу. Описано преобразование мономиальной задачи ГП в задачу ЛП. Рассказано об основных методах решения задач ГП с ограничениями. Все понятия объяснены на примерах.