|
Так это же динамическое программирование на основе математической индукции. |
Задача ГП с ограничениями
Постановка задачи
Перейдем к рассмотрению задач геометрического программирования с ограничениями. Пока мы ограничим наше рассмотрение канонической формой таких задач, когда требуется минимизировать некоторый позином при ограничениях, согласно которым значения других позиномов не должны превышать единицы:
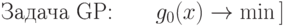
при ограничениях
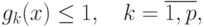

где
![g_{k}(x)=\sum\limits_{i\in
[k]}c_{i}\prod\limits_{j=1}^{m}{x_{j}}^{a_{ij}},\quad
k= \overline{0,p},\quad c_{i}>0,\ a_{ij}\in \mathbb{R}.](/sites/default/files/tex_cache/666d87e114b32fb1580251e98d9c31d1.png)
Поясним, что означает обозначение ![[k]](/sites/default/files/tex_cache/d67a02e18721ce594223364f961c793e.png) в приведенной выше
постановке задачи, на которую далее мы будем ссылаться как на задачу GP. Обозначим через
в приведенной выше
постановке задачи, на которую далее мы будем ссылаться как на задачу GP. Обозначим через  общее число мономов,
входящих в
общее число мономов,
входящих в 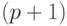 позином. Индексное множество
позином. Индексное множество ![I=[1,\ldots,n ]](/sites/default/files/tex_cache/3cc4e2e5313c1d7d7a7c89aa2e558751.png) нумерует их последовательно так, что первый моном позинома
нумерует их последовательно так, что первый моном позинома 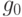 имеет номер
имеет номер  , а последний моном позинома
, а последний моном позинома 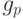 - номер
- номер  .
.
Будем обозначать через ![[k]](/sites/default/files/tex_cache/d67a02e18721ce594223364f961c793e.png) индексное подмножество,
соответствующее позиному
индексное подмножество,
соответствующее позиному 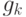 :
:
![I = [0]\cup[1]\cup\ldots\cup[p],\quad [k]\cap[l]=\emptyset, \
k\neq l.](/sites/default/files/tex_cache/567cb35f990801b7e9a991cd9e7a5b3b.png)
Обозначим через 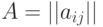 матрицу экспонент, состоящую из
матриц экспонент всех позиномов, входящих в задачу. Количество
строк в матрице
матрицу экспонент, состоящую из
матриц экспонент всех позиномов, входящих в задачу. Количество
строк в матрице  равно
равно  (числу мономов, входящих в
(числу мономов, входящих в 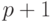 позином), число столбцов равно
позином), число столбцов равно  (числу переменных задачи).
Матрицу экспонент позинома
(числу переменных задачи).
Матрицу экспонент позинома 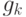 будем обозначать через
будем обозначать через ![A_{[k]},\ k=\overline{0,p}](/sites/default/files/tex_cache/17b30e9398581b86b1f4cbda17084c08.png) .
.
Обозначим через  вектор коэффициентов задачи,
состоящий из последовательно записанных векторов коэффициентов всех позиномов. Вектор
коэффициентов позинома
вектор коэффициентов задачи,
состоящий из последовательно записанных векторов коэффициентов всех позиномов. Вектор
коэффициентов позинома 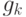 будем обозначать через
будем обозначать через ![c_{[k]},\
k=\overline{0,p}](/sites/default/files/tex_cache/fe9be3dd8ba057e942c2cd752291cbb8.png) .
.
Рассмотрим пример.
Пример 31 Запишем индексное множество, вектор коэффициентов и матрицу экспонент следующей задачи ГП:
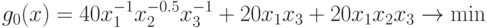 |
( 60) |
при ограничениях
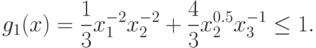 |
( 61) |
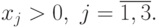 |
( 62) |
Запишем индексное множество задачи ГП. Индексное множество,
соответствующее целевой функции 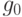 , состоящей из трех
мономов,
, состоящей из трех
мономов, ![[0] = \{1, 2, 3\}](/sites/default/files/tex_cache/6528abbeaa96054d9be3322d7ec42629.png) . Индексное множество,
соответствующее позиному
. Индексное множество,
соответствующее позиному 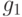 , состоящему из двух мономов,
, состоящему из двух мономов, ![[1] = \{4, 5\}](/sites/default/files/tex_cache/08cb749bca2a9dedb9dd721cb44f28a3.png) . Индексное множество задачи
(60)-(62)
. Индексное множество задачи
(60)-(62)
![I=[0]\cup[1] = \{1, 2, 3, 4, 5\}.](/sites/default/files/tex_cache/9d8c89b12f988feea00d3dd6e23f69ed.png)
Запишем теперь вектор коэффициентов задачи ГП. Вектор коэффициентов
целевой функции 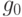
![c_{[0]} = (40, 20, 20),](/sites/default/files/tex_cache/38b119157b0bbdf3b5fe098a01f10702.png)
вектор коэффициентов ограничения 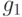
![c_{[1]} = (1/3, 4/3),](/sites/default/files/tex_cache/ea8bc9719efbf5bd55b4419fad06d8ec.png)
следовательно, вектор коэффициентов задачи (60)-(62)
![c = (c_{[0]}, %\cup%\bigcup
c_{[1]}) = (40, 20, 20, 1/3, 4/3).](/sites/default/files/tex_cache/c0747a9a6c0a11f78ed7b7599e8d997e.png)
Запишем матрицу экспонент задачи ГП. Матрица экспонент позинома 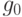
![A_{[0]}=\left\|
\begin{array}{rlr}
-1 & -0.5 & -1 \\
1 & \phantom{-}0 & 1 \\
1 & \phantom{-}1 & 1
\end{array}
\right\|,](/sites/default/files/tex_cache/09582b5cc2c28495bca2a1833cd1c159.png)
![A_{[1]}=\left\|
\begin{array}{rlr}
-2 & -2 & 0 \\
0 & \phantom{-}0.5 & -1
\end{array}
\right\|,](/sites/default/files/tex_cache/4c2c7722c81f5fc561a0924baa2e7521.png)
следовательно, матрица экспонент задачи (60)-(62)
![A =\left|\left|
\begin{array}{c}
A_{[0]} \\ A_{[1]}
\end{array}
\right|\right|
=
\left\|
\begin{array}{rlr}
-1 & -0.5 & -1 \\
1 & \phantom{-}0 & 1 \\
1 & \phantom{-}1 & 1 \\
-2 & -2 & 0 \\
0 & \phantom{-}0.5 & -1
\end{array}
\right\|.](/sites/default/files/tex_cache/c2f6739b54f38269558ce561e5cf275d.png)
Формула для вычисления степени трудности задачи ГП с ограничениями такая же, как для задачи ГП без ограничений:
 |
( 63) |
где  - общее число мономов во всех позиномах,
- общее число мономов во всех позиномах, 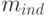 - число независимых переменных (определяемое рангом матрицы экспонент задачи
- число независимых переменных (определяемое рангом матрицы экспонент задачи  ).
).
Пример 32 Вычислим степень трудности для задачи ГП из примера 31.
Общее число мономов в задаче 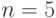 , можно показать, что число
независимых переменных
, можно показать, что число
независимых переменных  , следовательно, по формуле
(63)
, следовательно, по формуле
(63)  .
.
Прежде, чем перейти к изложению теории двойственности для задач ГП с ограничениями, покажем, как значение целевой функции из примера 31 может быть оценено с использованием ранее изложенной теории.
Пример 33 Оценим минимальное значение целевой функции 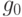 из примера
31.
из примера
31.
Рассмотрим соответствующую задачу ГП без ограничений:
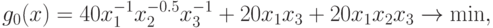

Легко заметить, что произведение переменных 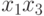 входит
во все мономы функции
входит
во все мономы функции 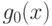 . Следовательно, мы можем
понизить размерность задачи на единицу, выполнив замену
. Следовательно, мы можем
понизить размерность задачи на единицу, выполнив замену 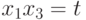 . Функцию, которая получится после выполнения
замены, обозначим через
. Функцию, которая получится после выполнения
замены, обозначим через 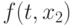 :
:
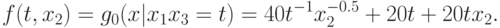
Функция 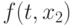 является регулярным позиномом (см.
"Регулярные позиномы"
), так как выполнены следующие равенства:
является регулярным позиномом (см.
"Регулярные позиномы"
), так как выполнены следующие равенства:
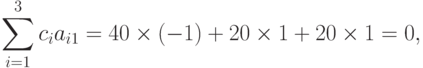
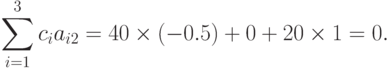
Из регулярности позинома 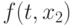 следует (см. теорему 5),
что его наименьшее значение, которое мы обозначим через
следует (см. теорему 5),
что его наименьшее значение, которое мы обозначим через 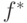 ,
вычисляется по формуле:
,
вычисляется по формуле:
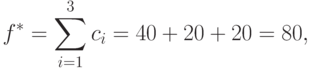
и достигается при 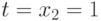 .
.
Выполнив обратную подстановку, получим, что точкой глобального
минимума функции 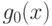 является любая точка вида
является любая точка вида
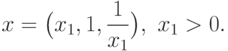 |
( 64) |
Вернемся к задаче
(60)-(62). Для этой
задачи величина 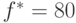 является нижней оценкой для
оптимального значения функции
является нижней оценкой для
оптимального значения функции 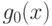 , так как при добавлении
ограничения значение минимума может только возрасти.
, так как при добавлении
ограничения значение минимума может только возрасти.
Проверим, существуют ли среди точек вида (64) такие, которые удовлетворяют ограничению (61):
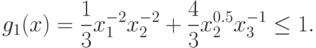
То есть необходимо проверить выполнение неравенства
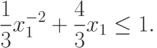
Данное неравенство не выполняется ни в одной точке, следовательно,
среди точек вида (64) нет таких, которые удовлетворяют
ограничению (61), и минимальное значение
целевой функции 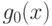 в задаче
(60)-(62) больше,
чем 80.
в задаче
(60)-(62) больше,
чем 80.
Замечание. В предложенном методе оценивания решения задачи (60)-(62) существенным является шаг понижения размерности задачи.
