|
Так это же динамическое программирование на основе математической индукции. |
Задача ГП без ограничений: двойственность
Решение задачи ГП при DOD>0
Покажем теперь, как двойственная задача с
положительной степенью трудности ( 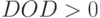 ) может быть переформулирована в
терминах базисных переменных.
) может быть переформулирована в
терминах базисных переменных.
Обозначим через  степень трудности задачи ГП. Тогда можно найти
базисные векторы
степень трудности задачи ГП. Тогда можно найти
базисные векторы 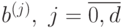 , так, что решение
системы ограничений двойственной задачи будет иметь вид
, так, что решение
системы ограничений двойственной задачи будет иметь вид
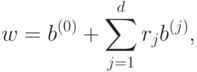
где  - базисные переменные,
удовлетворяющие условиям положительности
- базисные переменные,
удовлетворяющие условиям положительности
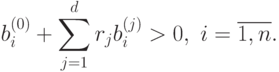 |
( 51) |
Вектор  удовлетворяет условиям ортогональности:
удовлетворяет условиям ортогональности:
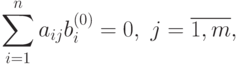 |
( 52) |
а также удовлетворяет условию нормальности
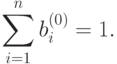 |
( 53) |
Выразим двойственную функцию через базисные переменные:
![v(r) =\prod\limits_{i=1}^{n}\left\{\frac{
c_{i}}{b_{i}^{(0)}+\sum\limits_{j=1}^{d}r_{j}b_{i}^{(j)}}\right\}^{\left[b_{i}^{(0)}+\sum\limits_{j=1}^{d}r_{j}b_{i}^{(j)}\right]}.](/sites/default/files/tex_cache/badeef741395622e0a4b4ec140b3cb76.png)
Таким образом, получили двойственную задачу в терминах базисных переменных:
![v(r) =\prod\limits_{i=1}^{n}\left\{\frac{
c_{i}}{b_{i}^{(0)}+\sum\limits_{j=1}^{d}r_{j}b_{i}^{(j)}}\right\}^{\left[b_{i}^{(0)}+\sum\limits_{j=1}^{d}r_{j}b_{i}^{(j)}\right]}\rightarrow
\max,](/sites/default/files/tex_cache/5559d162a2a9dc00c55a78c9c64f9b43.png) |
( 54) |
при ограничениях
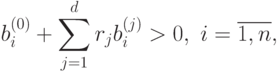 |
( 55) |
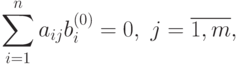 |
( 56) |
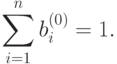 |
( 57) |
Приведем теорему, доказательство которой можно найти, например, в [5].
Теорема 8 Множество оптимальных решений задачи (54)--(57)
совпадает с множеством оптимальных решений задачи с целевой функцией,
равной 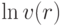 , при тех же ограничениях (55)--(57).
, при тех же ограничениях (55)--(57).
В качестве примера рассмотрим решение задачи ГП с 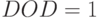 ,
поскольку для больших степеней трудности нахождение
векторов
,
поскольку для больших степеней трудности нахождение
векторов  требует использования специальных численных методов.
требует использования специальных численных методов.
Пример 30 Решим задачу ГП
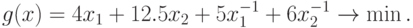
Матрица экспонент позинома
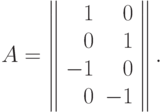
Степень трудности задачи равна  ,
следовательно, задача разрешима, но имеет не единственное
решение. Двойственная задача может быть переформулирована в
терминах базисных переменных. Поскольку
,
следовательно, задача разрешима, но имеет не единственное
решение. Двойственная задача может быть переформулирована в
терминах базисных переменных. Поскольку 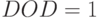 , то имеется одна
базисная переменная.
, то имеется одна
базисная переменная.
Двойственная задача имеет вид:
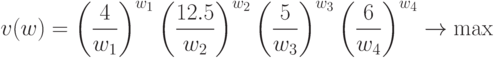
при ограничениях
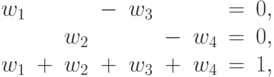 |
( 58) |

Сначала получим формулу общего решения системы (58).
Из первых двух уравнений системы следует, что  ,
,  . В качестве базисной выберем переменную
. В качестве базисной выберем переменную 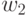 , тогда из третьего уравнения получаем
, тогда из третьего уравнения получаем 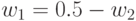 .
.
Положим 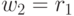 , тогда можно записать
, тогда можно записать
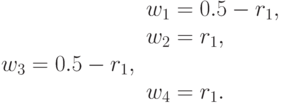 |
( 59) |
Запишем теперь систему (59) в векторном виде. Ведем следующие обозначения:
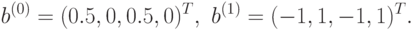
Тогда общее решение двойственной задачи примет вид:
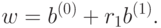
Проверим, что вектор  удовлетворяет условию
нормальности (53):
удовлетворяет условию
нормальности (53):
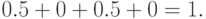
и условиям ортогональности (52):
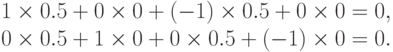
Для  должно выполняться условие положительности (51).
Из системы (59) следует, что оно выполняется при
должно выполняться условие положительности (51).
Из системы (59) следует, что оно выполняется при 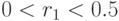 .
.
Подставив в формулу для функции 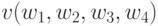 формулы
(59),
получим задачу максимизации функции
формулы
(59),
получим задачу максимизации функции  от одной переменной
от одной переменной 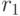 :
:
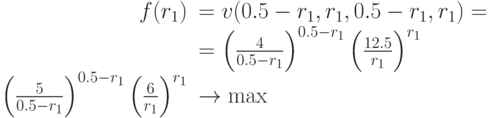
при ограничении
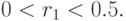
Упростив получившуюся формулу для функции 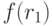 , получим задачу
, получим задачу
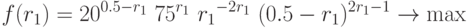
при ограничении
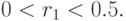
По теореме 8 вместо этой задачи можно решать задачу:

при ограничении
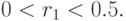
Упростив целевую функцию 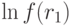 , получим задачу:
, получим задачу:

при ограничении
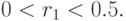
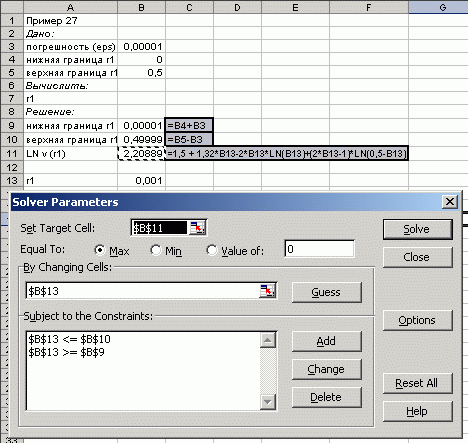
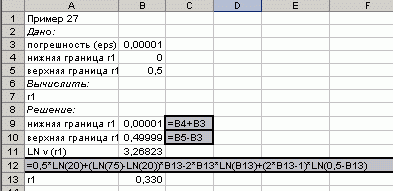
Решим получившуюся задачу при помощи надстройки Solver (Поиск решения) в программе Excel. На рис. 4.1 показано как ввести данные задачи. После нажатия на кнопку Solve (Решить) получим оптимальное решение и значение целевой функции (рис. 4.2):
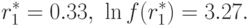
Из системы (59) находим оптимальное решение двойственной задачи:
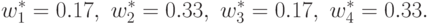
Максимальное значение двойственной функции вычисляем по следующей формуле:
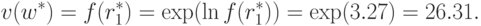
По теореме двойственности 7 справедливо равенство: 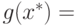
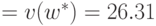 .
.
Вычислим теперь оптимальные значения переменных прямой задачи: 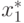 ,
, 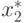 . Воспользуемся формулой
(39) для первых двух мономов:
. Воспользуемся формулой
(39) для первых двух мономов:
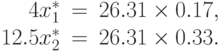
Отсюда получаем оптимальные значения переменных задачи: 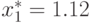 ,
, 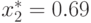 .
.
Краткие итоги
Сформулирована двойственная задача для задачи геометрического программирования без ограничений. Приведена формулировка теоремы двойственности. Введено понятие степени трудности задачи геометрического программирования. Все понятия и методы решения задачи ГП с помощью двойственной задачи продемонстрированы на примерах.