Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений
9.2. Сингулярно - возмущенные задачи
Рассмотрим простейшую нелинейную жесткую систему А.Н.Тихонова [9.5] (сингулярно - возмущенная задача Коши с малым параметром при производной):
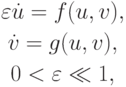
или
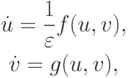
с начальными условиями
u(0) = u0, v(0) = v0.
Из характеристического уравнения находим:
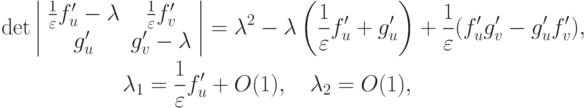
т.е. 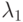 — жесткая, а
— жесткая, а 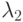 — мягкая часть спектра.
— мягкая часть спектра.
Первое, что хотелось бы сделать, — упростить задачу, положив 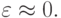 В этом случае система приобретает вид:
В этом случае система приобретает вид:
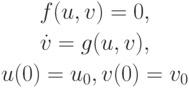
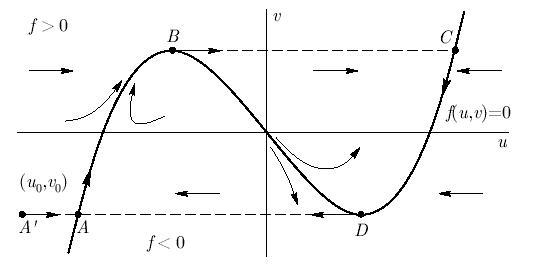
и описывает траекторию, проходящую по кривой f(u, v) = 0. Эта кривая играет существенную роль в решении исходной системы ОДУ. Однако полностью поведение решения упрощенная (невозмущенная) система описывать не будет, поскольку начальные данные не обязательно должны лежать на этой кривой.
Для того чтобы понять эту ситуацию, рассмотрим фазовый портрет конкретной системы ОДУ вида:
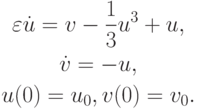
Эта система эквивалентна нелинейному уравнению второго порядка — уравнению Ван - дер - Поля. Приведенный выше вид иногда называется представлением Льенара. Подробнее о свойствах рассматриваемой задачи можно прочитать в [9.6], [9.7], [9.8], [9.9].
Кривая f(u, v) = 0 для этого случая изображена на рис. 9.4. Она делит плоскость {u, v} на две части: f > 0 и f < 0 ; вдали от кривой, поле скоростей {du, dv} направлено почти горизонтально влево (вправо) в зависимости от знака f. На самой кривой выделяются две устойчивые ветви AB и CD, где f'u < 0, и неустойчивая ветвь BD, на которой f'u > 0. Опишем теперь качественно поведение траектории рассматриваемой системы ОДУ, состоящей из следующих участков.