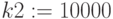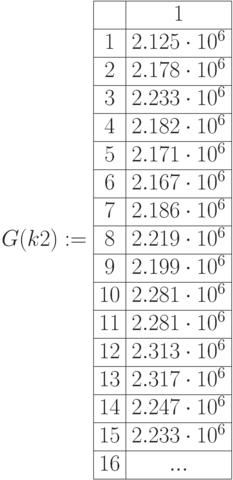| Россия |
Имитационное моделирование
Равномерное распределение количества заказов и нормального распределения стоимости заказа
В качестве первого сценария исследования прибыли выбираем следующее распределение входных данных.
- Изменение количества заказов в месяц
 - равномерное распределение на интервале
- равномерное распределение на интервале ![[a;b], \;a=-5%\; b=8%](/sites/default/files/tex_cache/518cedabb2b02a0c71b39611fd9421d1.png) .
. - Стоимость заказа
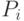 - нормально распределение со средним
- нормально распределение со средним 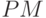 и средним квадратичным отклонением
и средним квадратичным отклонением 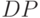
Нормальное распределение случайной величины характеризуется двумя параметрами: математическим ожиданием  и среднее квадратичным отклонением ?. Определяем вероятности возможных значений стоимостей заказов (см. таблицу 5.2) и рассчитываем среднее значение
и среднее квадратичным отклонением ?. Определяем вероятности возможных значений стоимостей заказов (см. таблицу 5.2) и рассчитываем среднее значение 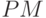 и среднее квадратичное отклонение
и среднее квадратичное отклонение 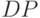 по формулам:
по формулам:
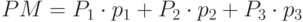
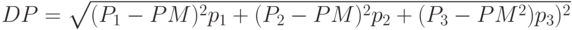 , где
, где 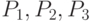 –значения
–значения  ,
, 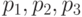 –вероятности (таблица 5.2).
–вероятности (таблица 5.2).
Имитационный эксперимент и статистический анализ результатов имитации
Проведем компьютерную имитацию значений параметров модели. Какой размер выборки выбрать для имитации? Целью имитационного моделирования является исследование множества реализаций случайной величины с целью определения её статистических характеристик и распределения этой случайной величины. Чем больше значений содержит случайная выборка, тем выше будет точность оценки интересующих нас характеристик. Введем количество реализаций как переменную  и сформируем случайные выборки
и сформируем случайные выборки 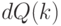 и
и 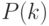 как функции количества реализаций. Изменение количества заказов
как функции количества реализаций. Изменение количества заказов 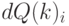 построим, используя функцию
построим, используя функцию 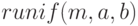 , которая создает вектор k случайных величин, имеющих равномерное распределение на интервале
, которая создает вектор k случайных величин, имеющих равномерное распределение на интервале ![[a,b],\; a <\; b](/sites/default/files/tex_cache/8f591ef1c5b8d67d42f3113a2b69646c.png) . Стоимость заказа
. Стоимость заказа 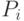 будет генерироваться как случайная совокупность с нормальным распределением с помощью функции
будет генерироваться как случайная совокупность с нормальным распределением с помощью функции 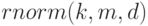 , которая генерирует вектор
, которая генерирует вектор  случайных величин, имеющих нормальное распределение с математическим ожиданием
случайных величин, имеющих нормальное распределение с математическим ожиданием  и дисперсией
и дисперсией  .
.
Листинг решения показан ниже. Массивы значений 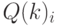 и
и 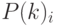 по месяцам
по месяцам  формируются в блоке программирования. При вычислении прибыли используется команда векторизации, которая перемножает элементы матриц. Массив
формируются в блоке программирования. При вычислении прибыли используется команда векторизации, которая перемножает элементы матриц. Массив  , сформированный в блоке программирования, представляет совокупность
, сформированный в блоке программирования, представляет совокупность  реализаций возможных значений исследуемого показателя - прибыли и отражает его случайную природу.
реализаций возможных значений исследуемого показателя - прибыли и отражает его случайную природу.
Входные данные
Количество заказов:

Стоимость: 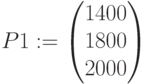
Вероятность: 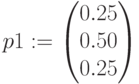
Затраты: 
Решение:
среднее значение стоимости:
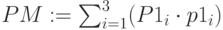
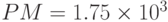
среднее квадратичное отклонение стоимости:
![DP:=\sqrt{\sum_{i=1}^{3}[(P1_i-PM)^2\cdot p1_i]}](/sites/default/files/tex_cache/bc2d0b9c5d810fac997dc14c4462ee62.png)
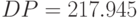
 – количество реализаций – размер случайной совокупности
– количество реализаций – размер случайной совокупности
Изменение количества заказов в месяц – равномерное распределение: 
Массив количества заказов по месяцам:  ,
, 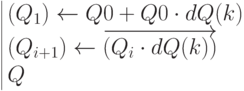
Массив стоимости заказа по месяцам:  ,
, 
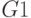 - прибыль в месяц,
- прибыль в месяц, 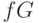 – затраты,
– затраты,  – массив суммарной прибыли за год
– массив суммарной прибыли за год
![G(k):=\begin{array}{|lc} for \; i\in 1..11 \\
\begin{array}{|lc}
G1_i \leftarrow \overrightarrow{[(P(k)_i)\cdot Q(k)_i]} \\
fG_i \leftarrow G1_i\cdot f \\
G2_i \leftarrow G1_i-fG_i
\end{array} \\
G \leftarrow \sum_{i=1}^{12}G2_i \\
G
\end{array}](/sites/default/files/tex_cache/6bf58ef541fc87c47c348ebbce92c299.png)
Статистический анализ результатов имитации
Для статистического и вероятностного анализа надо построить распределение и рассчитать статистические характеристики: среднее, максимальное и минимальное значения, среднеквадратичное отклонение, коэффициент вариации. Статистические показатели результирующей прибыли рассчитываются по статистическим функциям 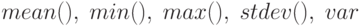 .
.
Расчет вероятности того, что прибыль будет меньше определенного значения, проводится по функции распределения – категория Probability Distribution.
Частотное распределение строится с использованием функции  (категория Statistics), которая строит матрицу гистограммы для bin сегментов разбиения интервала и вектора х случайных данных. Гистограмма прибыли построена для 500 сегментов разбиения интервала. Если сделать предположение, в соответствии с центральной предельной теоремой, что прибыль имеет нормальное распределение, можно провести расчет вероятности того, что прибыль будет меньше определенного значения, по функции распределения
(категория Statistics), которая строит матрицу гистограммы для bin сегментов разбиения интервала и вектора х случайных данных. Гистограмма прибыли построена для 500 сегментов разбиения интервала. Если сделать предположение, в соответствии с центральной предельной теоремой, что прибыль имеет нормальное распределение, можно провести расчет вероятности того, что прибыль будет меньше определенного значения, по функции распределения  . Рассчитанная вероятность события для прибыли принять значение меньше 2000000 составляет 1,3%
. Рассчитанная вероятность события для прибыли принять значение меньше 2000000 составляет 1,3%
Возможное значение суммарной прибыли для:
-
1000 реализаций:
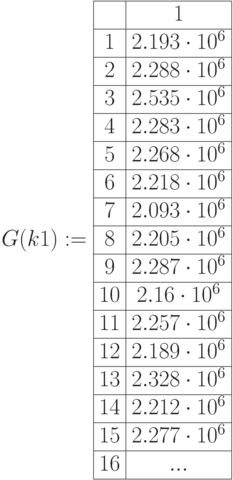
-
10000 реализаций: