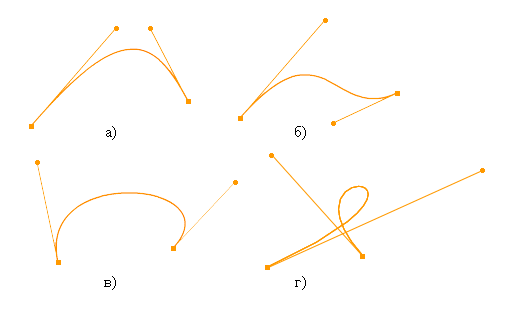| Беларусь, рогачёв |
Программное рисование во Flash MX
Квадратичный сплайн ( кривая Безье второго порядка, построенная по точкам A, C и B ), как видно на рисунке, в точках A и B касается исходной кривой, но в промежутке между этими точками существенно от нее отклоняется.
Чтобы аппроксимировать произвольную кривую квадратичными сплайнами (нарисовать ее с помощью операторов curveTo ), можно свести задачу к уже решенной: научиться аппроксимировать кубические сплайны квадратичными. Для этого прежде всего попробуем ответить на вопрос: сколько квадратичных сплайнов нужно для того, чтобы приблизить один кубический? Однозначного ответа на него не существует. Это зависит прежде всего от относительного расположения опорных и контрольных точек, а также от необходимой точности. В некоторых случаях приемлемый результат дает всего один сплайн. Однако бывает так, что, независимо от желаемой точности, обойтись одним сплайном принципиально невозможно. Так, например, из кривых, представленных на рис. 10.10, только первую (а) можно было бы аппроксимировать одним сплайном. Дело в том, что кривая Безье второго порядка не содержит перегибов (рис. 10.10б), поворотов больше чем на 180 градусов (рис. 10.10в) и самопересечений (рис. 10.10г), а это значит, что для кривых с рис. 10.10 б-г нужно как минимум по два квадратичных сплайна.
Рассмотрим более подробно случай, когда кубический сплайн заменяется одним квадратичным (все остальные случаи сводятся к нему разбивкой исходного сплайна на несколько более мелких).
Пусть у нас есть кривая Безье второго порядка:
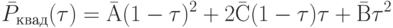
и третьего порядка (рис. 10.11):
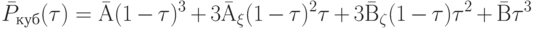
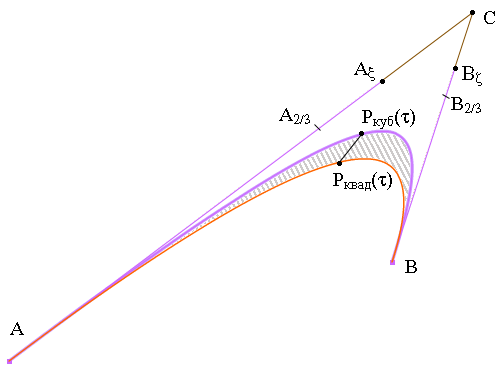
Подберем точку C так, чтобы кривая Pквад наиболее точно приближала кривую Pкуб. Очевидно, что это будет достигнуто, если в опорных точках кривые будут касаться друг друга. Поскольку в опорных точках направления касательных к кривым совпадают с направлением на ближайшую контрольную точку (это общее свойство кривых Безье ), то это значит, что отрезки 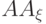 и AC, а также
и AC, а также  и BC должны совпадать. Иными словами, точка C - это точка пересечения прямых
и BC должны совпадать. Иными словами, точка C - это точка пересечения прямых 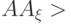 и
и  . И больше никак на выбор контрольной точки для квадратичного сплайна мы повлиять не можем. Теперь следует оценить точность приближения и, в случае необходимости, разбить кубический сплайн на два или более участка, и с каждым из них повторить вышеописанную процедуру.
. И больше никак на выбор контрольной точки для квадратичного сплайна мы повлиять не можем. Теперь следует оценить точность приближения и, в случае необходимости, разбить кубический сплайн на два или более участка, и с каждым из них повторить вышеописанную процедуру.
Дальше возникает вопрос: а как оценить точность приближения? Это можно сделать разными способами.
Так как точки A,  и С лежат на одной прямой, то можно записать, что
и С лежат на одной прямой, то можно записать, что
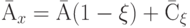 ,
,
где  - действительное число. Нетрудно видеть, что при
- действительное число. Нетрудно видеть, что при  точка
точка  совпадает с А, а при
совпадает с А, а при 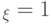 - с точкой С. Аналогично
- с точкой С. Аналогично
 .
.
Надо заметить, что  и
и  могут быть, вообще говоря, любыми: и большими единицы, и отрицательными. Если и
могут быть, вообще говоря, любыми: и большими единицы, и отрицательными. Если и 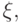 и
и  отрицательны, то кривая Pкуб выглядит так, как на рис. 10.10в, если знаки
отрицательны, то кривая Pкуб выглядит так, как на рис. 10.10в, если знаки  и
и  разные, это соответствует наличию точки перегиба (рис. 10.10б), если же
разные, это соответствует наличию точки перегиба (рис. 10.10б), если же
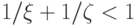 ,
,
то кривая имеет самопересечение (рис. 10.10г).
Если
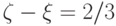 ,
,
то кривая 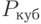 вырождается - сокращаются члены, содержащие
вырождается - сокращаются члены, содержащие 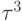 - и тождественно совпадает с Pквад. И чем больше
- и тождественно совпадает с Pквад. И чем больше  и
и  отличаются от 2/3 в ту или другую сторону, тем больше расхождение между кривыми. Однако этот метод расплывчат и мало информативен. В качестве меры расхождения между кривыми вернее всего было бы брать максимальное расстояние между ними. Но оно сложно считается, и разница будет не очень большой, если вместо него взять максимальное расстояние между точками на двух кривых при одном и том же значении параметра (на рис. 10.11 показаны точки
отличаются от 2/3 в ту или другую сторону, тем больше расхождение между кривыми. Однако этот метод расплывчат и мало информативен. В качестве меры расхождения между кривыми вернее всего было бы брать максимальное расстояние между ними. Но оно сложно считается, и разница будет не очень большой, если вместо него взять максимальное расстояние между точками на двух кривых при одном и том же значении параметра (на рис. 10.11 показаны точки  и
и  для
для 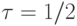 ). Можно также использовать площадь заштрихованного на рис. 10.11 участка (взятую по модулю), ее можно посчитать аналитически.
). Можно также использовать площадь заштрихованного на рис. 10.11 участка (взятую по модулю), ее можно посчитать аналитически.
Если условия работы программы такие, что отрисовка происходит намного медленнее, чем расчеты, то можно подумать над тем, как для каждого кубического сплайна обойтись не более чем двумя квадратичными. Для этого нужно оптимально подобрать значение параметра, по которому сплайн разбивается на две части - выбрать меру расхождения (например, площадь "щели" между кривыми), рассмотреть ее зависимость от точки разбиения и минимизировать. (Но бывают особые случаи: например, если есть точка перегиба, то разбивать нужно именно в ней, потому что участок, содержащий эту точку, приблизить квадратичным сплайном нельзя).
Однако такие ситуации, когда есть ресурсы для сложных расчетов, но надо экономить на рисовании объектов, встречаются довольно редко. Поэтому на практике эта задача решается следующим образом: если точность приближения недостаточна, сплайн разбивается на две части в точке 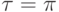 и дальше с каждой частью процедура повторяется. В таком случае получившихся кривых второго порядка может быть больше, чем при оптимальном выборе точки, но расчеты существенно упрощаются.
и дальше с каждой частью процедура повторяется. В таком случае получившихся кривых второго порядка может быть больше, чем при оптимальном выборе точки, но расчеты существенно упрощаются.
Но если перед вами стоит задача изобразить при помощи Флэш МХ кривую, заданную аналитически, то нет смысла прибегать к кривым Безье третьего порядка. Можно сразу использовать приближение квадратичными сплайнами. Ведь если у нас есть формула, задающая кривую (явно или параметрически), это значит, что мы можем узнать направление касательной в каждой точке. А если мы знаем направления касательных в двух не очень удаленных друг от друга точках, то мы можем соединить эти точки кривой при помощи оператора curveTo, передавая ему в качестве аргумента координаты точки пересечения касательных. Как, например, это было сделано в примере со спиралью (пример 10.8). Конечно, и здесь надо аккуратно обходить подводные камни: точки перегиба, изломы, самопересечения, повороты и другие подобные вещи. И можно попытаться разработать универсальный алгоритм разбиения произвольной кривой на точки, включающий в себя проверку точности приближения, обработку особых случаев и многое другое Но, как показывает опыт, гораздо удобнее и оптимальнее (с точки зрения и трудозатрат, и ресурсоемкости программы при ее выполнении - быстродействия, памяти и пр.) подбирать свой алгоритм для каждой конкретной задачи.