| Беларусь, рогачёв |
Программное рисование во Flash MX
Однако, кроме этих вышеперечисленных, для рисования линий во Флэш МХ существует еще один оператор: curveTo. Давайте разберемся, для чего он может понадобиться. Из References, да и просто из названия оператора, можно понять, что он нужен для рисования плавных кривых. Но так ли уж необходимо заводить для этого специальный оператор? Ведь, как видно из примеров 10.4 и 10.5, плавные кривые можно рисовать, пользуясь только lineTo.
Однако давайте посмотрим, что будет, если мы немного модифицируем код в примере 10.5 и заставим спираль вращаться. Для этого процесс рисования спирали перенесем в метод onEnterFrame, причем каждый раз будем поворачивать ее на небольшой угол (пример 10.6).
spir_mc.onEnterFrame = function(){
this.clear();
this.lineStyle(2, 0xcc00ff, 100);
if (curfr == undefined) curfr = 0
else curfr++;
for (var t=0; t<500; t++){
this.lineTo(0.25*t*Math.cos(0.1*t + 0.1*curfr),
-0.25*t*Math.sin(0.1*t + 0.1*curfr));
}
spir_mc.moveTo(0, 0);
for (var t=0; t<500; t++){
this.lineTo(-0.25*t*Math.cos(0.1*t + 0.1*curfr),
0.25*t*Math.sin(0.1*t + 0.1*curfr));
}
}
10.6.
Полюбуйтесь на вращающуюся спираль. У вас не закружилась голова? Тогда посмотрите на загрузку процессора... Дело в том, что в данном примере в каждом кадре тысячу раз вызывается оператор lineTo, следовательно, плееру приходится отображать тысячу отрезков, каждый из которых - отдельный объект.
Конечно, мы выбрали экстремальный случай, когда в каждом кадре нужно перерисовать всю картину. А это требуется не всегда. Так, в примере 10.7 моделируется поведение броуновской частицы, и на экране отображается траектория ее движения (рис 10.3 а). В этом случае в каждом кадре достаточно дорисовать отрезок траектории частицы, пройденный только за этот кадр, а всю картину перерисовывать не нужно. То есть, достаточно только одного оператора lineTo. Может быть, в этом случае загрузка процессора будет приемлемой? Однако, не тут-то было. Посмотрите на рисунок 10.3 б и в. Вверху (б) показан график зависимости длительности кадра от количества кадров, прошедших с момента запуска симуляции, а под ним (в) - график зависимости загрузки процессора от времени. (Конечно, отображение графика б добавляет в каждый кадр еще один вызов оператора lineTo, но качественно на характер картины это не влияет). Сначала длительность кадра постоянна - 33 миллисекунды (что соответствует номинальной скорости проигрывания 30 кадров в секунду). Но загрузка процессора в это время неуклонно возрастает. И когда она доходит до ста процентов, начинает возрастать длительность кадра. То есть, чем больше линий на экране, тем большее время тратится на перерисовку. Из этого можно сделать только один вывод: даже если картина почти не меняется (добавляется один отрезок в несколько пикселей), флэш-плеер все равно перерисовывает ее полностью.
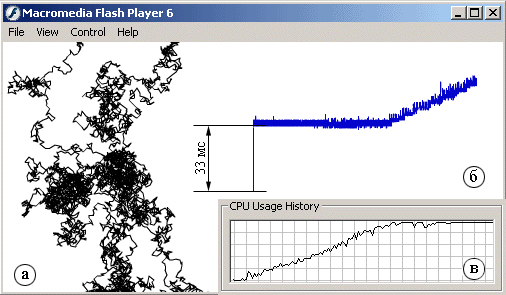
Рис. 10.3. Моделирование поведения броуновской частицы: а) Траектория движения модели броуновской" частицы (в каждом кадре меняющей направление своего движения), изображенная с помощью метода lineTo; б) график зависимости длительности кадра от номера кадра (тоже нарисованный с помощью lineTo); в) график зависимости загрузки процессора от времени при исполнении программы, отображающей кривые а) и б)
_root.createEmptyMovieClip("brown", 1);
_root.createEmptyMovieClip("timePlot", 2);
curX = 125; curY = 125;
brown.moveTo(curX, curY);
frame = 0;
timePlot._yscale = -100;
timePlot._y = 150;
timePlot._x = 250;
timePlot.lineStyle(1, 0x0000cc, 100);
time = getTimer();
brown.lineStyle(1, 0x000000, 100);
brown.onEnterFrame = function(){
curX += Math.round((Math.random() - 0.5)*10);
curX = curX > 250 ? 250 : ( curX < 0 ? 0 : curX);
curY += Math.round((Math.random() - 0.5)*10);
curY = curY > 250 ? 250 : ( curY < 0 ? 0 : curY);
brown.lineTo(curX, curY);
frame++;
deltaTime = getTimer() - time;
time = getTimer();
timePlot.lineTo(frame, 2*deltaTime);
if (timePlot._width > 250){
timePlot._xscale /=2;
}
}
10.7.
Можно ли как-то повлиять на эту ситуацию? В случае примера 10.7 - боимся, что никак. Разве что каким-нибудь образом убирать с экрана часть траектории. Однако, это случай экстремальный: действительно, здесь каждый нарисованный отрезок никак не связан с предыдущими, и предсказать его расположение невозможно.
В большинстве же случаев оптимизация все-таки возможна. Например, с помощью оператора curveTo. Давайте несколько модифицируем код из примера 10.5.
_root.createEmptyMovieClip("spir_mc", 1);
_root.createEmptyMovieClip("spirneg_mc", 2);
spir_mc._x = 275; spir_mc._y = 200;
spir_mc.lineStyle(3, 0xcc00ff, 100);
spirneg_mc._x = 275;
spirneg_mc._y = 200;
spirneg_mc.lineStyle(3, 0xcc00ff, 100);
alpha = 5;
dt = 1;
tmax = 50;
sindt = Math.sin(dt);
cosdt = Math.cos(dt);
cost = 1; sint = 0;
for (var t=0; t<tmax; t+=dt){
R1 = t*t*(cosdt - (t + dt)*sindt) - (t + dt)*(t + dt);
R2 = -t*t*(sindt + (t + dt)*cosdt) + t*(t + dt)*(t + dt);
factor = -alpha /( dt*cosdt + (t*(t+dt) + 1)*sindt);
xc = factor*(R1*cost + R2*sint);
yc = factor*(-R2*cost + R1*sint);
cost = Math.cos(t+dt); sint = Math.sin(t+dt);
xt = alpha*(t+dt)*cost; yt = alpha*(t+dt)*sint;
spir_mc.curveTo(xc, yc, xt, yt);
spirneg_mc.curveTo(-xc, -yc, -xt, -yt);
}
10.8.
В результате выполнения этого кода картинка получается точно такая же, как и в примере 10.5. Однако этот код выполняется в три раза быстрее.
Оператор curveTo позволяет не только ускорить работу программы, но и упростить ее. Так, цикл for из примера 10.4:
for (var tau=0; tau <=1; tau+=0.01) curve_mc.lineTo(2*xControl*tau*(1-tau) + xTarget*tau*tau, 2*yControl*tau*(1-tau) + yTarget*tau*tau);
может быть заменен одним оператором, как в следующем примере:
curve_mc.curveTo(xControl, yControl, xTarget, yTarget);10.9.
Конечно, пример 10.4 специально подобран так, чтобы curveTo так на него ложилась. Однако, почти любую гладкую кривую можно достаточно точно аппроксимировать, если грамотно пользоваться оператором curveTo.
