|
Хотелось бы иметь возможность читать текст сносок при использовании режима "Версия для печати" |
Элементы теории реляционных баз данных: функциональные зависимости и декомпозиция без потерь
Введение
Несмотря на свою практическую ориентированность, теория реляционных баз данных является самостоятельным научным направлением, в котором работали (и продолжают работать) многие известные исследователи, чьи имена будут встречаться в наших лекциях. Мы не планировали в данном курсе подробно описывать основные результаты в области теории реляционных баз данных. Наша цель состоит в том, чтобы обеспечить только определения и утверждения, необходимые для общего понимания процесса проектирования реляционных баз данных на основе нормализации.
Поскольку наиболее важные с практической точки зрения свойства реляционных баз данных базируются на понятии функциональной зависимости, мы выделили в отдельную лекцию краткое обсуждение соответствующих теоретических вопросов. Среди этих вопросов наибольший интерес представляют замыкания и покрытия множеств функциональных зависимостей, аксиомы Армстронга и теорема Хита о достаточном условии декомпозиции отношения без потерь. Понятия и утверждения данной лекции действительно нужны для усвоения материала лекции 7, но мы стремились еще и продемонстрировать читателям на несложных примерах, что собой представляет теория реляционных баз данных, каков уровень ее сложности и насколько она понятна интуитивно.
Заметим, что мы не выделяли в отдельные лекции теоретический материал, касающийся многозначных зависимостей и зависимостей соединения. Это было сделано по двум причинам. Во-первых, эти виды зависимостей реже встречаются при моделировании предметной области средствами баз данных. Поэтому мы сочли достаточным представить внутри лекции 8 только основы соответствующего теоретического материала. Во-вторых, хотя теория многозначных зависимостей и зависимостей соединения, по сути, не намного сложнее теории функциональных зависимостей, ее определения и утверждения слишком громоздки для данного курса.
Функциональные зависимости
Наиболее важные с практической точки зрения нормальные формы отношений основываются на фундаментальном в теории реляционных баз данных понятии функциональной зависимости. Для дальнейшего изложения нам потребуется несколько определений и утверждений (по ходу изложения мы будем пояснять их и иллюстрировать).
Общие определения
Пусть задана переменная отношения r, и X и Y являются произвольными подмножествами заголовка r ("составными" атрибутами).
В значении переменной отношения r атрибут Y функционально зависит от атрибута X в том и только в том случае, если каждому значению X соответствует в точности одно значение Y. В этом случае говорят также, что атрибут X функционально определяет атрибут Y ( X является детерминантом ( определителем ) для Y, а Y является зависимым от X ). Будем обозначать это как r.X->r.Y .
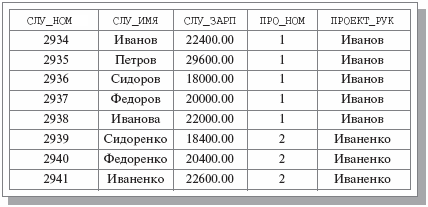
Для примера будем использовать отношение СЛУЖАЩИЕ_ПРОЕКТЫ {СЛУ_НОМ, СЛУ_ИМЯ, СЛУ_ЗАРП, ПРО_НОМ, ПРОЕКТ_РУК} (рис. 6.1). Очевидно, что если СЛУ_НОМ является первичным ключом отношения СЛУЖАЩИЕ, то для этого отношения справедлива функциональная зависимость (Functional Dependency – FD) СЛУ_НОМ->СЛУ_ИМЯ.
На самом деле, для тела отношения СЛУЖАЩИЕ_ПРОЕКТЫ в том виде, в котором оно показано на рис. 6.1, выполняются еще и следующие FD (1):
СЛУ_НОМ->СЛУ_ИМЯ
СЛУ_НОМ->СЛУ_ЗАРП
СЛУ_НОМ->ПРО_НОМ
СЛУ_НОМ->ПРОЕКТ_РУК
{СЛУ_НОМ, СЛУ_ИМЯ}->СЛУ_ЗАРП
{СЛУ_НОМ, СЛУ_ИМЯ}->ПРО_НОМ
{СЛУ_НОМ, СЛУ_ИМЯ}->{СЛУ_ЗАРП, ПРО_НОМ}
…
ПРО_НОМ->ПРОЕКТ_РУК и т.д.Поскольку имена всех служащих различны, то выполняются и такие FD (2):
СЛУ_ИМЯ->СЛУ_НОМ СЛУ_ИМЯ->СЛУ_ЗАРП СЛУ_ИМЯ->ПРО_НОМ и т.д.
Более того, для примера на рис. 6.1 выполняется и FD (3):
СЛУ_ЗАРП->ПРО_НОМ
Однако заметим, что природа FD группы (1) отличается от природы FD групп (2) и (3). Логично предположить, что идентификационные номера служащих должны быть всегда различны, а у каждого проекта имеется только один руководитель. Поэтому FD группы (1) должны быть верны для любого допустимого значения переменной отношения СЛУЖАЩИЕ_ПРОЕКТЫ и могут рассматриваться как инварианты, или ограничения целостности этой переменной отношения.
FD группы (2) базируются на менее естественном предположении о том, что имена всех служащих различны. Это соответствует действительности для примера из рис. 6.1, но возможно, что с течением времени FD группы (2) не будут выполняться для какого-либо значения переменной отношения СЛУЖАЩИЕ_ПРОЕКТЫ.
Наконец, FD группы (3) основана на совсем неестественном предположении, что никакие двое служащих, участвующие в разных проектах, не получают одинаковую зарплату. Опять же, данное предположение верно для примера из рис. 6.1, но, скорее всего, это случайное совпадение.
В дальнейшем нас будут интересовать только те функциональные зависимости, которые должны выполняться для всех возможных значений переменных отношений.
Заметим, что если атрибут A отношения r является возможным ключом, то для любого атрибута B этого отношения всегда выполняется FD A->B (в группе (1) к этим FD относятся все FD, детерминантом которых является СЛУ_НОМ ). Обратите внимание, что наличие в отношении СЛУЖАЩИЕ_ПРОЕКТЫ FD ПРО_НОМ->ПРОЕКТ_РУК приводит к некоторой избыточности этого отношения. Имя руководителя проекта является характеристикой проекта, а не служащего, но в нашем случае содержится в теле отношения столько раз, сколько служащих работает над проектом.
Итак, мы будем иметь дело с FD, которые выполняются для всех возможных состояний тела соответствующего отношения и могут рассматриваться как ограничения целостности. Как показывает (неполный) список (1), таких зависимостей может быть очень много. Поскольку они трактуются как ограничения целостности, за их соблюдением должна следить СУБД. Поэтому важно уметь сократить набор FD до минимума, поддержка которого гарантирует выполнение всех зависимостей. Мы займемся этим в следующих подразделах.
FD A->B называется тривиальной, если 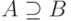 (т. е. множество атрибутов A включает множество B или совпадает с множеством B ).
(т. е. множество атрибутов A включает множество B или совпадает с множеством B ).
Очевидно, что любая тривиальная FD всегда выполняется. Например, в отношении СЛУЖАЩИЕ_ПРОЕКТЫ всегда выполняется FD {СЛУ_ЗАРП, ПРО_НОМ}->СЛУ_ЗАРП. Частным случаем тривиальной FD является A->A.
Поскольку тривиальные FD выполняются всегда, их нельзя трактовать как ограничения целостности, и поэтому они не представляют интереса с практической точки зрения. Однако в теоретических рассуждениях их наличие необходимо учитывать.