|
Хотелось бы иметь возможность читать текст сносок при использовании режима "Версия для печати" |
Проектирование реляционных баз данных на основе принципов нормализации: дальнейшая нормализация
Введение
Функциональные зависимости, о которых мы говорили в предыдущих двух лекциях, и нормальные формы, основанные на учете "аномальных" функциональных зависимостей, являются естественными и легко понимаемыми, поскольку в их основе лежит понятие функционального отображения, интуитивно понятного даже людям, далеким от математики. Конечно, было бы замечательно, если бы ликвидация в ходе нормализации аномальных функциональных зависимостей гарантировала отсутствие аномалий обновления отношений.
К сожалению, эта гарантия в общем случае не обеспечивается. Иногда в переменных отношений требуется поддержка более сложных ограничений целостности, для выражения которых понятие функции оказывается недостаточным. Класс зависимостей, опирающихся на понятие функционала – обобщение понятия функции, обнаружил в 1970-е гг. Рональд Фейджин. Он назвал такие зависимости многозначными, поскольку в них одному значению детерминанта соответствует множество значений зависимого атрибута. Наличие в переменной отношения многозначных зависимостей, не являющихся функциональными зависимостями от возможного ключа, приводит к аномалиям обновления таких отношений. Фейджин показал, что в этом случае возможна декомпозиция данных отношений на две проекции, для которых подобные аномалии обновления не проявляются. Такие проекции находятся в четвертой нормальной форме.
Позже было установлено, что при наличии некоторых естественных ограничений, являющихся обобщением ограничений многозначных зависимостей, и в отношениях, которые находятся в четвертой нормальной форме, проявляются аномалии обновления. Более того, эти аномалии невозможно устранить путем проецирования отношения на две проекции, требуется декомпозиция на три или большее число отношений. Такие ограничения получили название зависимостей проекции/соединения. Отношение, в котором существует нетривиальная зависимость проекции/соединения, может быть декомпозировано на три или большее число проекций, в которых зависимости проекции/соединения следуют из возможного ключа. Такие проекции находятся в пятой нормальной форме, или нормальной форме проекции/соединения. В отношениях, находящихся в пятой нормальной форме, отсутствуют аномалии обновления, которые можно было бы устранить путем декомпозиции, и поэтому при достижении пятой нормальной формы процесс проектирования реляционной базы данных на основе нормализации естественным образом завершается.
Многозначные зависимости и четвертая нормальная форма
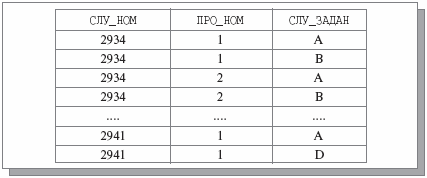
Чтобы перейти к вопросам дальнейшей нормализации, рассмотрим еще одну возможную (четвертую) интерпретацию переменной отношения СЛУЖ_ПРО_ЗАДАН. Предположим, что каждый служащий может участвовать в нескольких проектах, но в каждом проекте, в котором он участвует, им должны выполняться одни и те же задания. Возможное значение четвертого варианта переменной отношения СЛУЖ_ПРО_ЗАДАН показано на рис. 8.1.
Аномалии обновлений при наличии многозначных зависимостей и возможная декомпозиция
В новом варианте переменной отношения единственным возможным ключом является заголовок отношения {СЛУ_НОМ, ПРО_НОМ, СЛУ_ЗАДАН}. Кортеж <сн, пн, сз> входит в тело отношения в том и только в том случае, когда служащий с номером сн выполняет в проекте пн задание сз. Поскольку для каждого служащего указываются все проекты, в которых он участвует, и все задания, которые он должен выполнять в этих проектах, для каждого допустимого значения переменной отношения СЛУЖ_ПРО_ЗАДАН должно выполняться следующее ограничение ( ТСПЗ обозначает тело отношения):
IF (<сн, пн1, сз1> ТСПЗ AND <сн, пн2, сз2> ТСПЗ) THEN (<сн, пн1, сз2> ТСПЗ AND <сн, пн2, сз1> ТСПЗ)
Наличие такого ограничения (как мы скоро увидим, это ограничение порождается наличием многозначной зависимости ) приводит к тому, что при работе с отношением СЛУЖ_ПРО_ЗАДАН проявляются аномалии обновления.
- Добавление кортежа. Если уже участвующий в проектах служащий присоединяется к новому проекту, то к телу значения переменной отношения СЛУЖ_ПРО_ЗАДАН требуется добавить столько кортежей, сколько заданий выполняет этот служащий.
- Удаление кортежей. Если служащий прекращает участие в проектах, то отсутствует возможность сохранить данные о заданиях, которые он может выполнять.
- Модификация кортежей. При изменении одного из заданий служащего необходимо изменить значение атрибута СЛУ_ЗАДАН в стольких кортежах, в скольких проектах участвует служащий.
Трудности, связанные с обновлением переменной отношения СЛУЖ_ПРО_ЗАДАН, решаются путем его декомпозиции на две переменных отношений: СЛУЖ_ПРО_НОМ {СЛУ_НОМ, ПРО_НОМ} и СЛУЖ_ЗАДАНИЕ {СЛУ_НОМ, СЛУ_ЗАДАН}. Значения этих переменных отношений, соответствующие значению переменной отношения СЛУЖ_ПРО_ЗАДАН с рис. 8.1, показаны на рис. 8.2.
Легко видеть, что декомпозиция, представленная на рис. 8.2, является декомпозицией без потерь и что эта декомпозиция решает перечисленные выше проблемы с обновлением переменной отношения СЛУЖ_ПРО_ЗАДАН.
- Добавление кортежа. Если некоторый уже участвующий в проектах служащий присоединяется к новому проекту, то к телу значения переменной отношения СЛУЖ_ПРО_НОМ требуется добавить один кортеж, соответствующий новому проекту.
- Удаление кортежей. Если служащий прекращает участие в проектах, то данные о заданиях, которые он может выполнять, остаются в отношении СЛУЖ_ЗАДАНИЕ.
- Модификация кортежей. При изменении одного из заданий служащего необходимо изменить значение атрибута СЛУ_ЗАДАН в одном кортеже отношения СЛУЖ_ЗАДАНИЕ.