Лекция 6: Нормальные формы отношений. Создание логической модели реляционной базы данных
Нормальная форма Бойса-Кодда
3НФ упрощает решение проблем контроля избыточности данных, интерпретации нуль-значений, контроля за операциями модификации данных, только если в отношениях отсутствуют какие-либо другие ФЗ, в частности обратные ФЗ неключевого атрибута на один из атрибутов составного первичного ключа или многозначные ФЗ. В противном случае вышеперечисленные проблемы остаются неразрешенными. Для устранения таких проблем, связанных с существованием обратных ФЗ неключевых атрибутов на часть составного ключа, была предложена усиленная 3НФ или НФ Бойса-Кодда.
Отношение находится в нормальной форме Бойса-Кодда (НФБК), если оно находится в 3НФ, и в нем отсутствовали зависимости ключевых атрибутов от неключевых атрибутов. Иными словами, НФБК допускает наличие только таких нетривиальных ФЗ, в которых ключ определяет один или более других атрибутов:  , где
, где 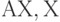 включает некоторый ключ.
включает некоторый ключ.
Таким образом, схема отношения в НФБК обладает теми же достоинствами, что и схема в 3НФ, но устраняет некоторые дополнительные аномалии, не устраняемые 3НФ. Например, в отношение (Город, Адрес, Почтовый_индекс), находящееся в 3НФ, невозможно записать кортеж для города с известным почтовым индексом, если не известен адрес с этим почтовым индексом. Данное отношение не находится в НФБК, так как имеет место ФЗ Почтовый_индекс -> Город, а атрибут почтовый_индекс не является ключом этого отношения.
Замечание. В отличие от 3НФ, исходные отношения не всегда могут быть приведены в НФБК.
Пример. Приведение отношения к НФБК
Продолжим рассмотрение примеров из области судоходства.
Допустим, что экипаж судна разделен на команды, каждая из которых отвечает за разные виды работ. Члены экипажа могут входить в разные команды, но в каждую команду входит только один руководитель. Команда может иметь несколько руководителей. Каждый член экипажа может руководить только одной командой. Отношение задается таблицей 6.1 ниже:
| Член экипажа | команда | Руководитель |
|---|---|---|
| Иванов | Наблюдение | Прохоров |
| Иванов | Питание | Макаров |
| Петров | Наблюдение | Леонтьев |
| Модин | Наблюдение | Прохоров |
| Васин | Питание | Лазарев |
| Фролов | Обслуживание | Сидоров |
| Ивлев | Обслуживание | Сидоров |
Отношение находится в 3НФ, однако содержит аномалию удаления. Если Петрова удалить из команды наблюдения, то будет потеряна информация о том, что Леонтьев является руководителем команды наблюдения, и при назначении нового члена экипажа в команду наблюдения не будет известно, что у нее есть еще один руководитель, кроме Прохорова.
Заметим, что в предыдущих случаях разбиение отношений происходило без создания избыточности данных из-за обратной зависимости атрибута на часть ключа. Приведение отношения к НФБК заключается в создании дополнительного отношения, содержащего сведения о руководителях команд (таблица 6.2).
| Команда | Руководитель |
|---|---|
| Наблюдение | Прохоров |
| Питание | Макаров |
| Наблюдение | Леонтьев |
| Питание | Лазарев |
| Обслуживание | Сидоров |
Результат приведения отношения КОМАНДА к НФБК представлен на рис. 6.5.
Четвертая нормальная форма
Отношение находится в четвертой нормальной форме (4НФ), если оно находится в 3НФ или НФБК и все независимые многозначные ФЗ разнесены в отдельные отношения с одним и тем же ключом. Иными словами, 4НФ применяется при наличии в отношении более чем одной многозначной ФЗ и требует, чтобы отношение не содержало независимых многозначных ФЗ.
Пример. Приведение к 4НФ
Рассмотрим отношение, содержащее сведения о кораблях (Ship), совершаемых ими рейсах (Voyage) и капитанах (Captain) (задано таблицей 6.3). Отношение представлено в таблице ниже и на рис. 6.6.
| Акбар | Иванов | Санкт-Петербург - Калининград |
| Акбар | Петров | Санкт-Петербург - Калининград |
| Акбар | Ивлев | Санкт-Петербург - Калининград |
| Акбар | Прохоров | Санкт-Петербург - Калининград |
| Акбар | Лазарев | Санкт-Петербург- Лондон |
| Акбар | Прохоров | Санкт-Петербург- Лондон |
| Жучка | Петров | Санкт-Петербург - Марсель |
| Жучка | Фролов | Санкт-Петербург - Стокгольм |
| Жучка | Ивлев | Санкт-Петербург - Стокгольм |
Отношение находится в НФБК и содержит только многозначные ФЗ. Однако имеет место аномалия удаления: если капитан Петров уйдет в отставку и все кортежи о нем будут удалены, то будут потеряны сведения о том, что корабль Жучка совершает рейсы Санкт-Петербург - Марсель. Если добавить новый рейс, то, возможно, придется ввести несколько кортежей в наше отношение.
Приведение отношения к 4НФ заключается в выделении для каждой многозначной ФЗ своего отношения, как показано на рис. 6.7.
Таким образом, процедура приведения отношения к 4НФ сводится к выполнению нескольких проекций, в данном случае двух проекций.




