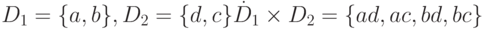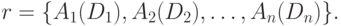Реляционная модель данных
Информация, данные, информационные системы
Понятие отношения
Реляционная модель данных была предложена Е.Ф. Коддом в 1970 году и получила к настоящему времени широкое распространение и популярность. Этому способствовали два ее существенных достоинства: 1) однородность представления данных в модели, которая обусловливает простоту восприятия ее конструкций пользователями базы данных, и 2) наличие развитой математической теории реляционных баз данных, которая обусловливает корректность ее применения.
В основе реляционной модели данных лежит понятие отношения, которое задается списком своих элементов и перечислением их значений. Рассмотрим пример на рис. 4.1. На нем представлено расписание движения автобусов по маршруту "Москва - Черноголовка - Москва". Налицо определенная структура. Каждый включенный в расписание рейс имеет свой номер, время отправления и время в пути. Расписание может быть представлено таблицей. Заголовки колонок таблицы носят название атрибутов. Список их имен носит названия схемы отношения. Каждый атрибут определяет тип представляемых им данных, который вместе с областью его значений называется доменом. Вся таблица целиком называется отношением, а каждая строка таблицы носит название кортежа отношения. Таким образом, отношение можно представить в виде двумерной таблицы.
Подходы к определению понятия отношения могут быть различными. Математически отношение может быть определено как множество кортежей, являющейся подмножеством декартова произведения фиксированного числа областей (доменов). В результате получаем, что в каждом кортеже должно быть одинаковое число компонент (атрибутов) и значение каждого из них выбирается из некоторого определенного домена.
Введем ряд математических определений, связанных с понятием отношения.
Определение 1. Декартово произведение Пусть D1, D2, ..., Dn - произвольные конечные множества, не обязательно различные. Декартовым произведением этих множеств
называется множество вида
Пример:
Определение 2. Схема отношения
Пусть
- имена атрибутов. Схемой r отношения R называется конечное множество имен атрибутов
Определение 3. Отношение
Отношением со схемой r на конeчных множествах D1, D2,…, Dn называется подмножество R декартового произведения
Элементы отношения (d1, d2, ..., dn), как уже упоминалось выше, называются кортежами. О каждом отношении, являющимся подмножеством декартового произведения 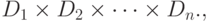 можно сказать, что оно имеет арность n. Кортеж (d1, d2, ..., dn) имеет n компонентов. Для обозначения кортежа применяется и сокращенная форма записи d1, d2, ..., dn. Использование понятия декартового произведения для определения отношения в реляционной модели данных делает модель конструктивной. На математическом языке это означает, что все остальные понятия модели определяются в рамках строго математического построения на базе декартового произведения.
можно сказать, что оно имеет арность n. Кортеж (d1, d2, ..., dn) имеет n компонентов. Для обозначения кортежа применяется и сокращенная форма записи d1, d2, ..., dn. Использование понятия декартового произведения для определения отношения в реляционной модели данных делает модель конструктивной. На математическом языке это означает, что все остальные понятия модели определяются в рамках строго математического построения на базе декартового произведения.
Табличная форма представления отношения была введена в целях популяризации модели среди неподготовленных пользователей баз данных. Трактовка реляционной теории на уровне таблиц скрывает ряд определений, важных для понимания как теории реляционных баз данных, так и языка манипулирования данными, моментов.
Во-первых, атрибуты разных отношений могут быть определены на одном домене, так же как и атрибуты одного отношения. Это очень важное обстоятельство, позволяющее устанавливать связи по значению между отношениями. Во-вторых, множество математически по своему определению не может иметь совпадающих элементов, и, следовательно, кортежи в отношении можно различить лишь по значению их компонент. Это тоже очень важное для модели обстоятельство: никакие два кортежа не могут иметь полностью совпадающих компонент. Таким образом, в реляционной модели полностью исключается дублирование данных о сущностях реального мира! В-третьих, заметим, что схема отношения также есть множество, что позволяет работать с ними с помощью теоретико-множественных операций. Это является важным моментом для построения теории проектирования реляционных схем баз данных.
Существует определенное различие между математическим определением отношения и действительным хранением отношений в памяти компьютера. По определению, отношение не может иметь два идентичных кортежа. Однако СУБД, поддерживающие реляционную модель данных, хранят отношения в файлах операционной системы компьютера. Размещение отношений в файлах операционной системы допускает хранение идентичных кортежей. Если не используется специальная техника (контроль целостности по первичному ключу ), то обычно большинство промышленных СУБД допускают хранение двух идентичных кортежей в базе данных.
С математической точки зрения однородность реляционной модели, о которой упоминалось выше, состоит в том, что схема отношения является постоянной, иначе говоря, каждая строка таблицы имеет один и тот же формат. С другой стороны, предполагается, что каждая строка таблицы представляет некую сущность реального мира или связь между ними. Обладают ли сущности реального мира такой однородной структурой, является вопросом, на который должен ответить аналитик или эксперт-пользователь. Решение о пригодности использования реляционной модели для моделирования данных конкретной предметной области решается руководителем ИТ-проекта и аналитиками.