|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Организационно-экономическая система управления материальными запасами промышленных корпоративных систем
О практическом применении классической модели управления запасами.Для отработки методики практического использования классической модели управления запасами проведен эксперимент на снабженческосбытовой базе, а именно на Реутовской химбазе Московской области. Собраны и обработаны данные по одному из товаров, распространяемых этой организацией в большом объеме, - по кальцинированной соде. В качестве исходной информации о спросе использовались данные об ежедневном отпуске кальцинированной соды потребителям, зафиксированные на карточках складского учета. Рассчитана величина затрат на хранение как соответствующая доля общей суммы издержек по содержанию базы, а также расходы на доставку новых партий. Для определения расходов на хранение запасов использованы данные о заработной плате складского персонала (включая основную и дополнительную заработную плату, начисления на зарплату), расходах на содержание охраны, эксплуатацию складских зданий и сооружений, расходах по текущему ремонту, по таре, на приемку , хранение, упаковку и реализацию товаров, о величине амортизационных отчислений и др. Для расчета расходов на доставку новых партий товара использованы данные о расходах по завозу, о плате за пользование вагонами и контейнерами сверх установленных норм, расходах на содержание и эксплуатацию подъемнотранспортных механизмов, о заработной плате работников, занятых в процессе доставки товара, канцелярских, почтовых и телеграфных расходах и др.
Полезным оказалось вытекающее из "принципа уравнивания погрешностей" соотношение (4.11). Интенсивность спроса \mu и погрешность определения этого параметра найдены методом наименьших квадратов. Это дало возможность установить величину относительной точности определения параметров модели, вытекающих из величин погрешностей исходных данных для спроса. Параметры классической модели управления запасами  и
и  оценивались двумя способами - по методике Всесоюзного института материальнотехнического снабжения и по методике Центрального экономико-математического института АН СССР. Для каждой из методик с помощью соотношения (6.11) были найдены абсолютные погрешности определения параметров
оценивались двумя способами - по методике Всесоюзного института материальнотехнического снабжения и по методике Центрального экономико-математического института АН СССР. Для каждой из методик с помощью соотношения (6.11) были найдены абсолютные погрешности определения параметров  и
и  . Оказалось, что для каждой из методик интервалы
. Оказалось, что для каждой из методик интервалы 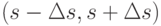 и
и 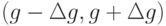 таковы, что числа, рассчитанные по альтернативной методике, попадают внутрь этих интервалов. Это означает, что для определения параметров
таковы, что числа, рассчитанные по альтернативной методике, попадают внутрь этих интервалов. Это означает, что для определения параметров  и
и  можно пользоваться любой из указанных методик (в пределах точности расчетов, заданной наблюдаемыми колебаниями спроса).
можно пользоваться любой из указанных методик (в пределах точности расчетов, заданной наблюдаемыми колебаниями спроса).
Вызванное отклонениями параметров модели в допустимых пределах максимальное относительное увеличение суммарных затрат на доставку и хранение продукции не превосходило 26% (колебания по кварталам от 22,5 до 25,95%). Фактические издержки почти в 3 раза превышали оптимальные (в зависимости от квартала фактические издержки составляли от 260 до 349% от оптимального уровня). Следовательно, внедрение модели Вильсона в практику управления запасами на Реутовской химбазе дает возможность снизить издержки, связанные с доставкой и хранением кальцинированной соды, не менее чем в 2 раза [11, 4].
Таким образом, несмотря на то, что параметры модели определены неточно и отклонения значений параметров (от тех значений, по которым рассчитывается оптимальный план поставок) приводят к некоторому увеличению затрат по сравнению с затратами в оптимальном плане, использование рассматриваемой модели для реального управления запасами конкретной продукции может дать значительный экономический эффект. Аналогичным является положение со многими другими моделями управления запасами. Это утверждение подтверждает и зарубежный опыт [11].
Двухуровневая модель управления запасами.Создание любой автоматизированной системы управления материальнотехническим снабжением (в другой терминологии - процессами логистики), базирующейся на комплексе экономико-математических моделей, должно включать в себя разработку (в качестве блоков) моделей деятельности отдельных баз (складов). Поэтому большое внимание уделяется проблеме построения оптимальной политики управления запасами на базе (складе). Экономико-математическую теорию удается развивать в основном для однопродуктовых моделей.
Двухуровневая модель управления запасами - это однопродуктовая модель работы склада, в которой заявки потребителей удовлетворяются мгновенно. При отсутствии продукта заявки учитываются. Как только запас на складе опускается до уровня  , мгновенно поступает партия товара величиной
, мгновенно поступает партия товара величиной  и запас на складе оказывается равным
и запас на складе оказывается равным  .Как и в рассмотренном выше варианте классической модели Вильсона с дефицитом, издержки складываются из издержек по хранению, издержек от дефицита и издержек по доставке. Средние издержки за время
.Как и в рассмотренном выше варианте классической модели Вильсона с дефицитом, издержки складываются из издержек по хранению, издержек от дефицита и издержек по доставке. Средние издержки за время  имеют вид
имеют вид
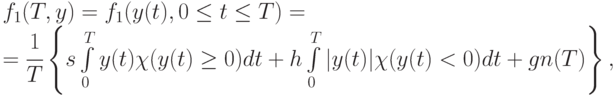
где 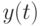 - уровень запаса на складе,
- уровень запаса на складе, 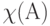 - индикатор множества
- индикатор множества  , т. е.
, т. е.  при
при 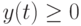 и
и  при
при 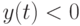 , в то время как
, в то время как  при
при 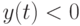 и
и  при
при 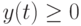 , параметры модели
, параметры модели  ,
,  ,
, 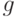 имеют тот же смысл, что и выше. Оптимизация состоит в определении значений нижнего уровня
имеют тот же смысл, что и выше. Оптимизация состоит в определении значений нижнего уровня  и верхнего уровня
и верхнего уровня  , минимизирующих средние издержки.
, минимизирующих средние издержки.
В 1950-х гг. американский исследователь К. Эрроу (в будущем - нобелевский лауреат по экономике) с сотрудниками показал, что в ряде случаев оптимальная политика управления запасами - это политика, основанная на двухуровневой модели [11]. Этот принципиально важный теоретический результат стимулировал развитие исследований свойств двухуровневой модели. Однако окончательная теория была построена только в конце 1970-х годов [11].
Важными являются характеристики потока заявок. Пусть 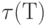 - число заявок за время
- число заявок за время  . Эта величина предполагается случайной. С прикладной точки зрения вполне естественно предположить, что математическое ожидание
. Эта величина предполагается случайной. С прикладной точки зрения вполне естественно предположить, что математическое ожидание 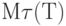 конечно. Накопленный спрос за время
конечно. Накопленный спрос за время  имеет вид
имеет вид
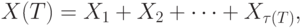
где 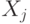 - величина
- величина  -й заявки. Предполагается, что
-й заявки. Предполагается, что  - последовательность независимых одинаково распределенных случайных величин с математическим ожиданием
- последовательность независимых одинаково распределенных случайных величин с математическим ожиданием  . Таким образом, накопленный спрос за время
. Таким образом, накопленный спрос за время  является суммой случайного числа случайных слагаемых. Накопленный спрос определяет уровень запаса на складе, поэтому математический аппарат изучения двухуровневой модели - это предельная теория сумм случайного числа случайных слагаемых.
является суммой случайного числа случайных слагаемых. Накопленный спрос определяет уровень запаса на складе, поэтому математический аппарат изучения двухуровневой модели - это предельная теория сумм случайного числа случайных слагаемых.
При некоторых условиях регулярности (выполняющихся для реальных систем управления запасами) в [11] найдены оптимальные (для горизонта планирования  ) значения нижнего и верхнего уровней:
) значения нижнего и верхнего уровней:
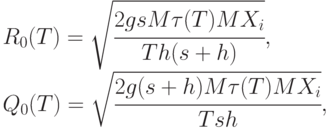
Часто можно принять, что число поступающих заявок обладает некоторой равномерностью. Например, вполне естественно принять, что
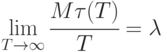
при некотором  . Здесь
. Здесь 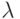 - параметр, описывающий предельную интенсивность спроса. Тогда асимптотически оптимальные уровни имеют вид:
- параметр, описывающий предельную интенсивность спроса. Тогда асимптотически оптимальные уровни имеют вид:
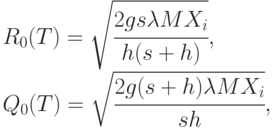
Отметим, что асимптотическое распределение уровня запаса на складе - равномерное на отрезке ![[R, R + Q]](/sites/default/files/tex_cache/57f8684690296f808d5774e69ad05a29.png) .
.
Модель планирования размеров поставок на базу (склад).В двухуровневой модели накопленный спрос в любой момент времени - случайная величина. Это не всегда соответствует экономической реальности. Достаточно часто в соответствии с заключенными договорами размеры поставок на базу и объемы запрашиваемой потребителями продукции определены до начала года (с разбивкой по кварталам или по месяцам) и затем не меняются. Однако поставщик имеет право отгружать продукцию, а потребители - забирать ее в течение всего квартала (или месяца).
Опишем соответствующую однопродуктовую модель [10]. Пусть интервал планирования разбит на  периодов, не обязательно одинаковых по продолжительности. В течение каждого периода приходит на базу одна поставка. В
периодов, не обязательно одинаковых по продолжительности. В течение каждого периода приходит на базу одна поставка. В  -й период ее величина равна
-й период ее величина равна 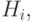 а момент поступления - случайная величина
а момент поступления - случайная величина 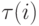 с функцией распределения
с функцией распределения 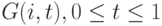 , где
, где  - отношение времени, прошедшего с начала
- отношение времени, прошедшего с начала  -го периода, к продолжительности его,
-го периода, к продолжительности его, 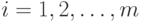 .
.
В  -й период имеется
-й период имеется 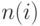 потребителей, получающих с базы строго определенное количество продукта,
потребителей, получающих с базы строго определенное количество продукта, 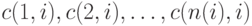 соответственно. Моменты поступления требований от потребителей - случайные величины
соответственно. Моменты поступления требований от потребителей - случайные величины 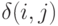 ,
, 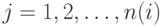 ,
, 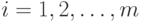 , с функциями распределения
, с функциями распределения 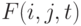 ,
, 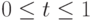 , где
, где  - отношение времени, прошедшего после начала соответствующего периода, к продолжительности этого периода. Если в момент прихода требования на базе имеется достаточное количество продукта, то он отпускается мгновенно. Если продукта нет, потребителю придется ждать очередной поставки. Если продукта недостаточно, то весь оставшийся товар отпускается сейчас же, а оставшуюся часть приходится ждать.
- отношение времени, прошедшего после начала соответствующего периода, к продолжительности этого периода. Если в момент прихода требования на базе имеется достаточное количество продукта, то он отпускается мгновенно. Если продукта нет, потребителю придется ждать очередной поставки. Если продукта недостаточно, то весь оставшийся товар отпускается сейчас же, а оставшуюся часть приходится ждать.
В течение  -го периода,
-го периода, 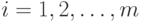 , все моменты поступления товара и требований
, все моменты поступления товара и требований 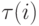 ,
, 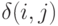 ,
, 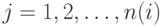 , предполагаются независимыми в совокупности. Потери, как обычно, складываются из издержек по хранению и от дефицита (расходы на доставку партий заданы заранее, т. е. постоянны, а потому их можно не включать в минимизируемый функционал). Издержки по хранению предполагаются пропорциональными времени хранения и величине запаса с коэффициентами пропорциональности
, предполагаются независимыми в совокупности. Потери, как обычно, складываются из издержек по хранению и от дефицита (расходы на доставку партий заданы заранее, т. е. постоянны, а потому их можно не включать в минимизируемый функционал). Издержки по хранению предполагаются пропорциональными времени хранения и величине запаса с коэффициентами пропорциональности 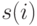 ,
, 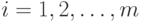 . Издержки от дефицита складываются из потерь у каждого из потребителей; они пропорциональны величине и длительности дефицита с коэффициентами пропорциональности
. Издержки от дефицита складываются из потерь у каждого из потребителей; они пропорциональны величине и длительности дефицита с коэффициентами пропорциональности 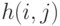 ,
, 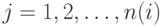 ,
, 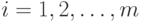 .
.
Пусть 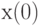 - начальный запас,
- начальный запас, 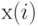 - количество продукта на базе в конце
- количество продукта на базе в конце  -го периода,
-го периода, 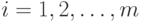 . Пусть
. Пусть 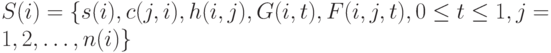 - исходные данные модели в
- исходные данные модели в  -й период. Как легко видеть, математическое ожидание издержек за
-й период. Как легко видеть, математическое ожидание издержек за  -й период зависит только от
-й период зависит только от  ,
, 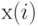 и
и  . Для краткости обозначим его через
. Для краткости обозначим его через 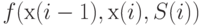 . Тогда математическое ожидание издержек за
. Тогда математическое ожидание издержек за  периодов равно
периодов равно
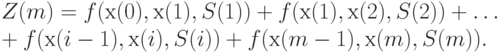 |
( m))) |
Необходимо минимизировать 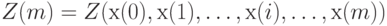 по совокупности переменных. Таким образом, необходимо найти оптимальные значения уровней запаса на складе в начале и в конце периодов. Это эквивалентно определению оптимальных размеров поставок по периодам и начального запаса. Ограничения рассматриваемой оптимизационной задачи выписаны в [11, 10].
по совокупности переменных. Таким образом, необходимо найти оптимальные значения уровней запаса на складе в начале и в конце периодов. Это эквивалентно определению оптимальных размеров поставок по периодам и начального запаса. Ограничения рассматриваемой оптимизационной задачи выписаны в [11, 10].
Вначале была сделана попытка рассматривать задачу минимизации 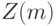 как задачу динамического программирования и решать ее типовыми методами. Однако вычислительных мощностей оказалось недостаточно для выполнения расчетов. Тогда нам удалось показать, что функция
как задачу динамического программирования и решать ее типовыми методами. Однако вычислительных мощностей оказалось недостаточно для выполнения расчетов. Тогда нам удалось показать, что функция 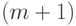 -го переменного
-го переменного 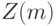 в действительности является суммой
в действительности является суммой 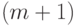 функции одного переменного.
функции одного переменного.
Действительно,
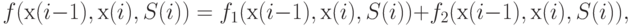
где 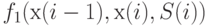 - математическое ожидание затрат, произведенных до прихода очередной поставки,
- математическое ожидание затрат, произведенных до прихода очередной поставки, 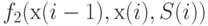 - математическое ожидание затрат после поступления поставки.
- математическое ожидание затрат после поступления поставки.
Ясно, что 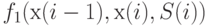 определяется запасом на начало периода и спросом до прихода поставки, но не зависит от запаса на конец периода, т. е. от
определяется запасом на начало периода и спросом до прихода поставки, но не зависит от запаса на конец периода, т. е. от 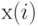 . Таким образом, можно записать, что
. Таким образом, можно записать, что
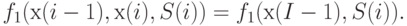 |
( i )) |
Пусть 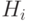 - объем поставки на склад в
- объем поставки на склад в  -й период. Сразу же после прихода поставки запас
-й период. Сразу же после прихода поставки запас 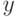 на складе равен
на складе равен
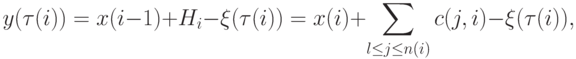 |
( i ))) |
где 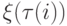 - накопленный с начала периода спрос. Поскольку
- накопленный с начала периода спрос. Поскольку 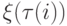 не зависит от
не зависит от 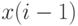 , то и
, то и 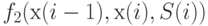 не зависит от
не зависит от 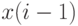 . Итак,
. Итак,
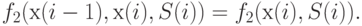 |
( i ))) |
Следовательно, минимизируемая функция имеет вид
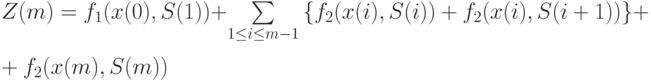 |
( m),S(m)) |
При этом ограничения наложены на каждую переменную 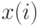 по отдельности [11, 10]. Ясно, что задача минимизации
по отдельности [11, 10]. Ясно, что задача минимизации 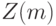 распадается на
распадается на 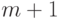 задачу минимизации функций одной переменной:
задачу минимизации функций одной переменной:
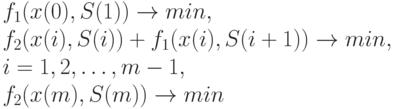 |
( 4.13) |
(ограничения не указаны). Следовательно, 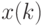 зависит только от исходных данных смежных периодов
зависит только от исходных данных смежных периодов  и
и 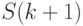 и остается неизменным при любом изменении
и остается неизменным при любом изменении  ,
, 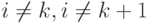 . Из указанного разложения задачи многомерной оптимизации на ряд задач одномерной оптимизации вытекает также, что при планировании на
. Из указанного разложения задачи многомерной оптимизации на ряд задач одномерной оптимизации вытекает также, что при планировании на 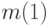 и
и 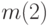 периодов совпадают оптимальные значения начального запаса и поставок за первые
периодов совпадают оптимальные значения начального запаса и поставок за первые 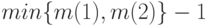 периодов. В частном случае стационарного режима
периодов. В частном случае стационарного режима 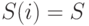 ,
, 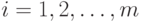 , оптимальный план имеет вид
, оптимальный план имеет вид 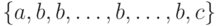 , где
, где  - решение первой из указанных в (4.13) задач,
- решение первой из указанных в (4.13) задач,  - решение второй задачи и
- решение второй задачи и  - третьей.
- третьей.
Переход к задачам (4.13) не только позволяет решить исходную задачу минимизации (напомним, что для минимизации задачи в исходной форме не хватало вычислительных мощностей), но также получить весьма важный для экономической интерпретации вывод о независимости оптимальных значений поставок и начального запаса от горизонта планирования  .
.
Важное замечание 4.Рассмотренная модель дает хороший пример пользы математического анализа оптимизационной задачи принятия решений. Такой анализ позволяет решать задачу не стандартными методами, требующими больших вычислительных ресурсов, а с помощью специально разработанных алгоритмов, учитывающих специфику задачи и позволяющих на много порядков сократить вычисления. Плата за экономию вычислительных ресурсов - необходимость квалифицированного труда специалистов по экономико-математическим методам и прикладной математике.
В настоящее время логистика - одна из экономических дисциплин, весьма развитая в теоретическом и практическом отношении. В ней рассматривается масса конкретных моделей управления запасами. Из перспективных направлений назовем использование случайных множеств в моделях логистики. Моделирование с целью нахождения оптимальных решений продемонстрировано выше на примерах системы моделей, исходящих из классической модели Вильсона, двухуровневой модели, модели оптимизации объемов поставок на базу (склад).

