|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Повышение эффективности корпоративных производственно-сбытовых структур (ПСС) в области сбыта и товаропродвижения
Задача решается известными из прикладной математики способами в зависимости от условий и имеет оптимальное решение. Алгоритмы решения подобных задач разделяются на три группы.
К первой группе относятся алгоритмы, основанные на методе последовательного улучшения плана. Сюда включается метод потенциалов (модифицированный распределительный метод), основанный на втором алгоритме метода улучшения плана, распределительный метод, использующий первый алгоритм метода последовательного улучшения плана.
Во вторую группу алгоритмов включаются: венгерский метод в различных модификациях; метод условно оптимальных планов, разработанный Ю.А. Олейником и А. Л. Лурье.
В третью группу входят алгоритмы одновременного исправления и плана и оценок (потенциалов).
Углубление в эти математические алгоритмы в данной лекции не делается, так как они известны из общей теории. Алгоритмы решения в каждом конкретном случае будут иметь разную структуру, а область поиска значительно сужена. Данная лекция посвящена принципам постановки подобных оптимизационных задач, а не описанию известных математических методов.
Последние достижения в области вычислительной техники привели к существенному упрощению поиска решения математических оптимизационных задач путем элементарного перебора. С помощью средств Microsoft Excel можно без труда найти решения оптимизируемых функций. Основное - грамотно и правильно поставить и описать оптимизационную задачу.
В случае отсутствия некоторых ограничений задача имеет множество решений. Дальнейший выбор из альтернатив следует тогда проводить с учетом остальных критериев, а также субъективных факторов.
Данный метод известен из общей теории логистики. Он применяется при предварительной оценке эффективности системы сбыта для рынка товаров как промышленного назначения, так и народного потребления не с чистой конкуренцией, когда нет точных данных по сбыту, вариативности цены и делается ряд серьезных допущений. Для толкающих систем метод можно применять достаточно условно, а для систем, построенных на логистических концепциях тянущего типа, применять не следует ввиду отсутствия временного фактора.
Метод 2.
Модель также рассматривается статически, т. е. за определенный промежуток времени. Добавляются ограничения по пропускным способностям, которые известны из вариантов классической "транспортной задачи".
Тогда добавляется еще одно условие:
Для 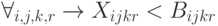
где 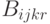 - пропускная способность коммуникации, т. е. количество изделий вида
- пропускная способность коммуникации, т. е. количество изделий вида  , которое может быть перемещено из звена
, которое может быть перемещено из звена  системы уровня
системы уровня  в пункт
в пункт  уровня
уровня  за определенный промежуток времени.
за определенный промежуток времени.
Это условие математически можно без труда трансформировать в другой вид в зависимости от внешних и внутренних факторов. Можно ввести коэффициенты и суммирование по видам изделий, зависящие от специфики реализуемых товаров, их объема, транспортных средств и расстояний. Задача без труда составляется в зависимости от вышеперечисленных обстоятельств.
Данный метод применяется в тех же случаях, что и первый. Задача становится более объемной, учитывает транспортную составляющую, что делает ее более актуальной.
Метод 3.
Делается жесткий акцент на условие, что часть товара при отсутствии дальнейших звеньев сбытовой цепи не реализовывается. Эта постановка задачи необходима для четкого отражения потерь в натуральных объемах реализации в случае отсутствия дальнейших звеньев сбытовой цепи.
К данным по каждому элементу цепи добавляется величина:
 - реальный объем реализации товара
- реальный объем реализации товара  в
в  -м магазине уровня
-м магазине уровня  , причем
, причем
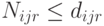
Вводится коэффициент 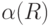 , лежащий в отрезке
, лежащий в отрезке ![[0; 1]](/sites/default/files/tex_cache/f083648758df2ddf9560f0b17ac28d3b.png) , - коэффициент, показывающий потерю объемов реализации при
, - коэффициент, показывающий потерю объемов реализации при 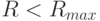
Таким образом, реальный объем реализации 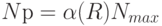 . Увеличение звеньев сбытовой структуры приводит в общем случае к повышению
. Увеличение звеньев сбытовой структуры приводит в общем случае к повышению 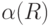 , а с другой стороны и к повышению затрат на создание структуры.
, а с другой стороны и к повышению затрат на создание структуры.
Целевая функция тогда примет следующий вид:
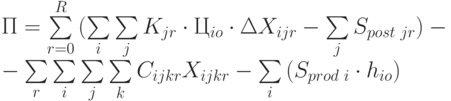 |
( 6.13) |
где
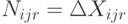 , если
, если 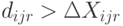 (завоз товара меньше запроса);
(завоз товара меньше запроса);
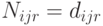 , если
, если 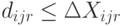 (товара завезено больше, чем запрошено);
(товара завезено больше, чем запрошено);
Во втором случае в каждом пункте  сбытовой системы остается нереализованного товара на величину
сбытовой системы остается нереализованного товара на величину 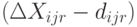 .
.
Такая постановка задачи применима при разработке системы розничных точек на определенной территории, а также при создании крупнооптовой региональной сети в различных регионах страны, особенно для рынка товаров народного потребления в условиях как чистой, так и монополистической конкуренции. То есть когда каждый новый элемент сбытовой структуры значительно повышает объемы реализации продукции. Используя данный метод, можно определить потери в спросе.
Метод 4.
Модель рассматривается статически. Добавляется характеристика территорий по налогообложению предприятий.
Прибыль каждого элемента системы облагается налогом в зависимости от местного закона по налогообложению. С другой стороны, расходы на создание оффшора значительно увеличат смету построения структуры сбыта.
Вводится характеристика
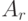 - нормированный коэффициент, определяющий величину оставшейся после уплаты налога прибыли (на уровне системы
- нормированный коэффициент, определяющий величину оставшейся после уплаты налога прибыли (на уровне системы  ).
).
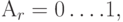 т. е. при ставке налога в 30%, у предприятия остается 70%, коэффициент
т. е. при ставке налога в 30%, у предприятия остается 70%, коэффициент  .
.
Целевая функция примет следующий вид:
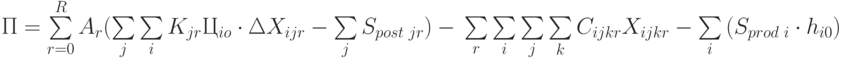 |
( 6.14) |
Данный метод используется при моделировании системы с оффшорным посредником или когда происходит выбор территории для создания промежуточного регионального склада для любого типа рынка. Как и все предыдущие методы, его не следует применять для разработки систем, построенных на концепции тянущего типа.
Метод 5.
Модель рассматривается динамически. Выбирается единица времени  (день, час, месяц). Ко всем показателям в вышеперечисленных формулах добавляется индекс
(день, час, месяц). Ко всем показателям в вышеперечисленных формулах добавляется индекс
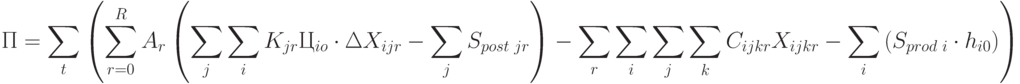 |
( 6.15) |
Ограничения задаются аналогично прошлым вариантам.
Поставленную задачу можно свести к задаче оценки инвестиционных проектов с помощью финансовых критериев, т. к. это позволяет оценить реальную прибыль с учетом временного фактора.
С введением параметра времени данная формула определения прибыли сводится к показателю 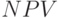 (чистой приведенной стоимости проекта) [2, 4, 10]. Для его расчета необходимо сформировать диаграммы денежных потоков ( CF - Cash Flow ) по каждому временному интервалу и определить коэффициент дисконтирования. Как известно из теории финансовой логистики:
(чистой приведенной стоимости проекта) [2, 4, 10]. Для его расчета необходимо сформировать диаграммы денежных потоков ( CF - Cash Flow ) по каждому временному интервалу и определить коэффициент дисконтирования. Как известно из теории финансовой логистики:
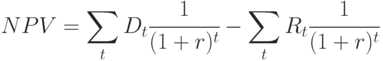 |
( 6.16) |
где 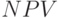 - чистая текущая стоимость проекта;
- чистая текущая стоимость проекта;
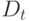 - все поступления денежных средств в период
- все поступления денежных средств в период  ;
;
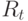 - все расходы и капиталовложения в период
- все расходы и капиталовложения в период  ;
;
 - коэффициент дисконтирования.
- коэффициент дисконтирования.
Моментом приведения является первый период, коэффициент дисконтирования выбирается исходя из экономического состояния государства, инфляции и средней банковской ставки.
На основе прогнозируемого по вышеописанной методике спроса и цены можно рассчитать приближенные денежные потоки, определяющие величину 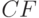 [10] по каждому периоду.
[10] по каждому периоду.
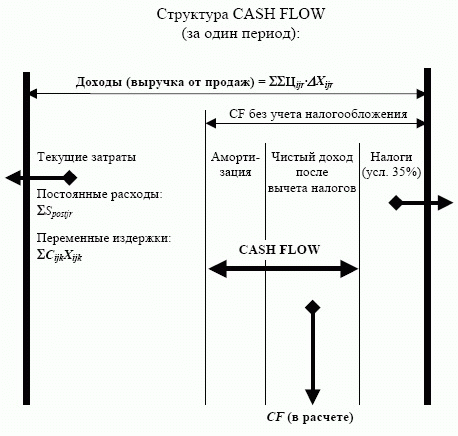
В общем виде структура денежных потоков предприятия выглядит следующим образом (рис. 6.20):
Исходя из предварительно рассчитываемых показателей 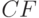 по каждому периоду времени на основе прогнозируемых объемов реализации и цен, определяется величина
по каждому периоду времени на основе прогнозируемых объемов реализации и цен, определяется величина 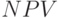 для анализируемого временного интервала. Амортизация - фиктивный денежный поток (не связанный с "живыми" деньгами). Ее доля в себестоимости продукции зависит от объема реализации и от принятой нормы амортизации, поэтому к переменным затратам ее относить нецелесообразно, а ее величина в постоянных затратах является условной. В показатель
для анализируемого временного интервала. Амортизация - фиктивный денежный поток (не связанный с "живыми" деньгами). Ее доля в себестоимости продукции зависит от объема реализации и от принятой нормы амортизации, поэтому к переменным затратам ее относить нецелесообразно, а ее величина в постоянных затратах является условной. В показатель 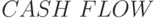 амортизация не включается. Поэтому затраты на создание системы (инвестиции) можно рассматривать отдельно в начальные периоды (
амортизация не включается. Поэтому затраты на создание системы (инвестиции) можно рассматривать отдельно в начальные периоды ( 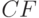 будет отрицательным) и не показывать в расчетах амортизацию финансовых вложений по последующим периодам.
будет отрицательным) и не показывать в расчетах амортизацию финансовых вложений по последующим периодам.
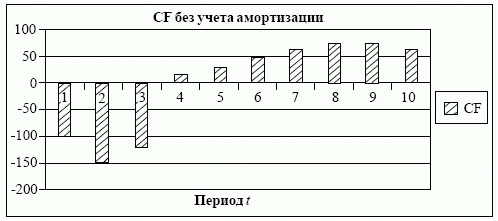
В общем виде диаграмма результирующих финансовых потоков по периодам времени проекта (с учетом дисконтирования) выглядит следующим образом (рис. 6.21).
Напомним, что
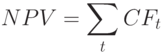
Задача сводится к нахождению таких  , чтобы
, чтобы 
Ограничения задаются аналогично, как в прошлых методах.
Данный метод можно применять для широкого спектра типов рынков как промышленного назначения, так и народного потребления с любой конкуренцией. Задача может быть расширена путем ввода дополнительных ограничений и применима для любой логистической концепции ввиду учета временного фактора. Показатель прогнозируемой прибыли становится точнее, а сам процесс моделирования правдоподобнее и целесообразнее и может использоваться для расчета бизнеспланов.
Таким образом, на первоначальном этапе можно отобрать определенное количество альтернативных схем по созданию сбытовой структуры предприятия путем моделирования по любому из вышеизложенных методов. Для каждого значения количества уровней в сбытовой системе с помощью решения оптимизационной задачи отбирается альтернативный вариант построения сбытовой структуры по критерию максимума 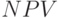 или прибыли (в упрощенном варианте). В случае рассмотрения проекта по инвестированию в систему сбыта, предварительный отбор можно вести и по другим критериям оценки финансовых вложений. Это: рентабельность; срок окупаемости инвестиций; отношение дисконтированных доходов к дисконтированным расходам и др.
или прибыли (в упрощенном варианте). В случае рассмотрения проекта по инвестированию в систему сбыта, предварительный отбор можно вести и по другим критериям оценки финансовых вложений. Это: рентабельность; срок окупаемости инвестиций; отношение дисконтированных доходов к дисконтированным расходам и др.
После определения всех критериев оценки вариантов предложенных сбытовых систем возникает задача выбора оптимального варианта.
Для решения задачи выбора варианта сбытовой системы из предложенных целесообразно использование системного анализа как объективного инструмента упорядочения и синтезирования субъективных суждений человека и расчетных показателей. Наиболее известные методы - метод средних баллов и метод медианы Кемени [13, 14], а также метод Дельфи и метод анализа иерархий (метод Саати). О последних двух методах расскажем ниже. Также существуют и другие экспертные методы, которые выбираются в зависимости от постановки каждой конкретной задачи: метод комиссии, метод суда, метод мозговой атаки [13, 14].
Метод Дельфи - метод установления экспертных суждений о явлениях, которые трудно измерить объективно и оценить в классическом смысле [11], - формализованная процедура получения и сбора в единое целое групповых суждений. Для получения и обработки суждений экспертов используется процедура анонимного анкетного опроса и последующего нахождения искусственного консенсуса. Метод предполагает полный отказ от коллективных обсуждений. В методе Дельфи принимаются специальные меры, чтобы исключить влияние на конечный результат экспертов, обладающих даром убеждать других [3]. Прямые дебаты в данном методе заменены тщательно разработанной программой последовательных индивидуальных опросов, проводимых обычно в форме анкетирования. Ответы экспертов обобщаются и вместе с новой дополнительной информацией поступают в распоряжение экспертов, после чего они уточняют свои первоначальные ответы. Такая процедура повторяется несколько раз до достижения приемлемой сходимости совокупности высказанных мнений. Недостатки метода Дельфи: значительное время, требуемое на повторение большого числа итераций экспертизы; необходимость неоднократного пересмотра экспертом своих ответов, что вызывает у него отрицательную реакцию.
Метод анализа иерархий [22] является систематизированной процедурой для иерархического представления элементов, определяющих суть любой проблемы. Решение задачи есть процесс поэтапного установления приоритетов расчетных критериев. Метод анализа иерархий базируется на следующих принципах, определяющих этапы проведения системного анализа:
- принципе идентичности и декомпозиции (создание структурной модели системы);
- принципе сравнительных суждений (построение "матрицы суждений");
- синтезе приоритетов (вычисление удельных весов каждого из вариантов и определение приоритетов).
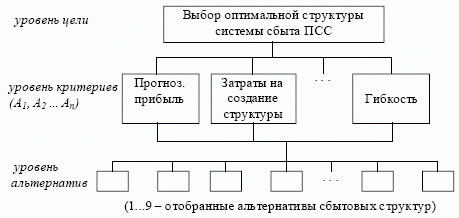
Полезен принцип идентичности и декомпозиции. На данном этапе происходит структурирование проблемы в виде иерархии или сети. Иерархия строится от вершины (цели - с точки зрения управления) через промежуточные уровни (критерии) к самому низкому уровню (который обычно является уровнем альтернатив). В данном примере структурирование проблемы имеет смысл провести в виде доминантной иерархии (см. рис. 6.22):
Иерархия должна быть полной, т. е. каждый элемент заданного уровня должен функционировать как критерий для всех элементов нижестоящего уровня. Закон иерархической непрерывности требует, чтобы элементы низшего уровня иерархии были сравнимы попарно по отношению к элементам следующего уровня и т. д. вплоть до вершины иерархии.