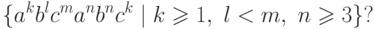| Помогите решить задание лекции 3 курс Математическая теория формальных языков |
Основные свойства контекстно-свободных языков
9.2*. Лемма о разрастании для линейных языков
Определение 9.2.1. Линейная грамматика в нормальной форме -
это такая линейная грамматика, в которой
каждое правило имеет вид  ,
, 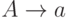 ,
,  или
или  ,
где
,
где 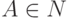 ,
, 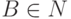 ,
,  .
.
Теорема 9.2.2. Каждая линейная грамматика эквивалентна некоторой линейной грамматике в нормальной форме.
Теорема 9.2.3. Если линейный язык не содержит пустого слова, то он порождается
некоторой линейной грамматикой в нормальной форме
без  - правил.
- правил.
Теорема 9.2.4. Язык L является линейным
тогда и только тогда, когда
язык 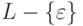 является линейным.
является линейным.
Лемма 9.2.5. Пусть L - линейный язык над алфавитом  . Тогда найдется такое положительное целое число p, что для любого слова
. Тогда найдется такое положительное целое число p, что для любого слова 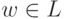 длины не меньше p можно подобрать слова
длины не меньше p можно подобрать слова 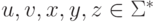 , для которых верно uvxyz = w,
, для которых верно uvxyz = w, 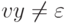 ( то есть
( то есть 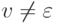 или
или 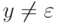 ),
), 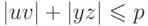 и
и 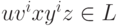 для всех
для всех 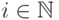 .
.
Доказательство.
Пусть язык 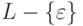 порождается линейной грамматикой в нормальной форме
порождается линейной грамматикой в нормальной форме 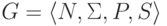 без
без  -правил.
Положим p = |N| + 1.
Пусть
-правил.
Положим p = |N| + 1.
Пусть 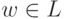 и
и  .
Зафиксируем некоторое дерево вывода слова w
в грамматике G.
Рассмотрим самый длинный путь в этом дереве
(он начинается с корня и заканчивается некоторым листом,
помеченным символом из
.
Зафиксируем некоторое дерево вывода слова w
в грамматике G.
Рассмотрим самый длинный путь в этом дереве
(он начинается с корня и заканчивается некоторым листом,
помеченным символом из  ).
Этот путь содержит не менее |N| + 1
вершин, помеченных элементами N.
Среди первых |N| + 1
вершин рассматриваемого пути
найдутся две вершины
с одинаковыми метками.
Выберем слова u, v, x, y и z
так, что uvxyz = w,
поддерево с корнем в одной из найденных вершин имеет крону x
и поддерево с корнем в другой найденной вершине имеет крону vxy.
).
Этот путь содержит не менее |N| + 1
вершин, помеченных элементами N.
Среди первых |N| + 1
вершин рассматриваемого пути
найдутся две вершины
с одинаковыми метками.
Выберем слова u, v, x, y и z
так, что uvxyz = w,
поддерево с корнем в одной из найденных вершин имеет крону x
и поддерево с корнем в другой найденной вершине имеет крону vxy.
Пример 9.2.6.
Рассмотрим язык 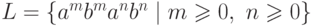 над алфавитом {a,b}.
Утверждение леммы 9.2.5
не выполняется ни для какого натурального числа p.
Следовательно, язык L
не является линейным.
над алфавитом {a,b}.
Утверждение леммы 9.2.5
не выполняется ни для какого натурального числа p.
Следовательно, язык L
не является линейным.
Упражнение 9.2.7. Какому классу принадлежит язык
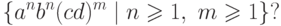
Упражнение 9.2.8. Какому классу принадлежит язык

Упражнение 9.2.9. Какому классу принадлежит язык