| Помогите решить задание лекции 3 курс Математическая теория формальных языков |
Основные свойства контекстно-свободных языков
В "лекции 2" были доказаны лемма о разрастании и свойства замкнутости класса автоматных языков. Некоторые из этих теорем имеют аналоги для класса контекстно-свободных языков (разделы 9.1 и 9.4), но этот класс не замкнут относительно дополнения и пересечения (раздел 9.5).
Лемма о разрастании для контекстно-свободных языков формализует явление "периодичности" в этих языках. Для полноты картины в разделах 9.2* и 9.3 приведены некоторые аналогичные теоремы для класса линейных языков, хотя ни в теории, ни в практических приложениях класс линейных языков значительной роли не играет.
В разделе 9.6 доказывается, что пересечение контекстно-свободного языка с автоматным языком является контекстно-свободным. В сочетании с леммой о разрастании этот факт дает удобное средство, позволяющее во многих задачах доказать, что заданный язык не является контекстно-свободным. Еще одно необходимое условие контекстной свободности сформулировано в разделе 9.7*.
9.1. Лемма о разрастании для контекстно-свободных языков
Лемма 9.1.1 (pumping lemma, лемма о разрастании, лемма о накачке,
лемма-насос) Пусть L - контекстно-свободный язык над
алфавитом  . Тогда найдется такое положительное целое число p, что для любого слова
. Тогда найдется такое положительное целое число p, что для любого слова 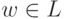 длины не меньше p можно подобрать слова
длины не меньше p можно подобрать слова 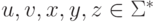 , для которых верно uvxyz = w,
, для которых верно uvxyz = w, 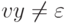 ( то есть
( то есть 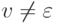 или
или 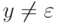 ),
), 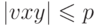 и
и 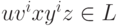 для всех
для всех 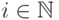 .
.
Доказательство.
Пусть язык  порождается грамматикой в нормальной форме Хомского
порождается грамматикой в нормальной форме Хомского 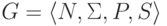 .
Индукцией по k
легко доказать, что для любого дерева вывода в грамматике G
длина кроны дерева не превышает 2k-2,
где k - количество вершин в самом длинном пути,
начинающемся в корне дерева и заканчивающемся в некоторой вершине,
помеченной символом из
.
Индукцией по k
легко доказать, что для любого дерева вывода в грамматике G
длина кроны дерева не превышает 2k-2,
где k - количество вершин в самом длинном пути,
начинающемся в корне дерева и заканчивающемся в некоторой вершине,
помеченной символом из  .
.
Положим p = 2|N|.
Пусть 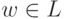 и
и  .
Зафиксируем некоторое дерево вывода с кроной w
в грамматике G.
Рассмотрим самый длинный путь в этом дереве.
Этот путь содержит не менее |N| + 2
вершин.
Среди них найдутся две вершины
с одинаковыми метками, причем их можно выбрать
среди последних |N| + 2
вершин рассматриваемого пути.
Выберем слова u, v, x, y и z
так, что uvxyz = w,
поддерево с корнем в одной из найденных вершин имеет крону x
и поддерево с корнем в другой найденной вершине имеет крону vxy.
.
Зафиксируем некоторое дерево вывода с кроной w
в грамматике G.
Рассмотрим самый длинный путь в этом дереве.
Этот путь содержит не менее |N| + 2
вершин.
Среди них найдутся две вершины
с одинаковыми метками, причем их можно выбрать
среди последних |N| + 2
вершин рассматриваемого пути.
Выберем слова u, v, x, y и z
так, что uvxyz = w,
поддерево с корнем в одной из найденных вершин имеет крону x
и поддерево с корнем в другой найденной вершине имеет крону vxy.
Из того что G -
грамматика в нормальной форме Хомского,
заключаем, что 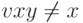 .
Неравенство
.
Неравенство  следует из того, что
самый длинный путь в соответствующем слову vxy
поддереве содержит не более |N| + 2
вершин. Для каждого
следует из того, что
самый длинный путь в соответствующем слову vxy
поддереве содержит не более |N| + 2
вершин. Для каждого 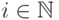 можно построить дерево вывода с кроной uvixyiz,
комбинируя части исходного дерева вывода.
можно построить дерево вывода с кроной uvixyiz,
комбинируя части исходного дерева вывода.
Пример 9.1.2.
Рассмотрим язык 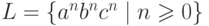 над алфавитом {a,b,c}.
Утверждение леммы 9.1.1
не выполняется ни для какого натурального числа p.
Действительно,
если uvxyz = apbpcp, |vy| > 0
и
над алфавитом {a,b,c}.
Утверждение леммы 9.1.1
не выполняется ни для какого натурального числа p.
Действительно,
если uvxyz = apbpcp, |vy| > 0
и 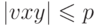 ,
то |vy|a = 0
или |vy|c = 0.
Следовательно, |uvvxyyz|a = p
или |uvvxyyz|c = p.
Так как |uvvxyyz| > 3p,
то
,
то |vy|a = 0
или |vy|c = 0.
Следовательно, |uvvxyyz|a = p
или |uvvxyyz|c = p.
Так как |uvvxyyz| > 3p,
то  .
Из этого можно заключить, что язык L
не является контекстно-свободным.
.
Из этого можно заключить, что язык L
не является контекстно-свободным.
Теорема 9.1.3. Каждый контекстно-свободный язык над однобуквенным алфавитом является автоматным.
Доказательство.
Пусть дан контекстно-свободный язык L
над алфавитом {a}.
Согласно лемме 9.1.1
найдется такое натуральное число p,
что множество 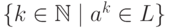 является объединением некоторого семейства
арифметических прогрессий,
причем у каждой прогрессии первый член и шаг не больше числа p.
Так как существует лишь конечное число прогрессий натуральных чисел
с таким ограничением,
рассматриваемое семейство конечно.
Следовательно, язык L
является автоматным
(используем пример 2.1.18).
является объединением некоторого семейства
арифметических прогрессий,
причем у каждой прогрессии первый член и шаг не больше числа p.
Так как существует лишь конечное число прогрессий натуральных чисел
с таким ограничением,
рассматриваемое семейство конечно.
Следовательно, язык L
является автоматным
(используем пример 2.1.18).
Упражнение 9.1.4. Является ли контекстно-свободным язык 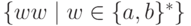 ?
?
Упражнение 9.1.5. Является ли контекстно-свободным язык 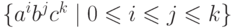 ?
?
Упражнение 9.1.6. Является ли контекстно-свободным язык 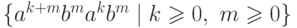 ?
?
Упражнение 9.1.7. Является ли контекстно-свободным язык {am | m простое}?
Упражнение 9.1.8. Является ли контекстно-свободным язык 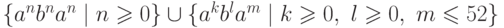 ?
?
Упражнение 9.1.9. Является ли контекстно-свободным язык  ?
?
Упражнение 9.1.10. Является ли контекстно-свободным язык 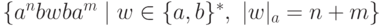 ?
?
Упражнение 9.1.11. Является ли контекстно-свободным язык  ?
?
Упражнение 9.1.12. Является ли контекстно-свободным язык  ?
?
Упражнение 9.1.13. Является ли контекстно-свободным язык {akbmcn | k < max(m,n)}?
Упражнение 9.1.14. Является ли контекстно-свободным язык {akbmcn | k > max(m,n)}?
Упражнение 9.1.15. Является ли контекстно-свободным язык
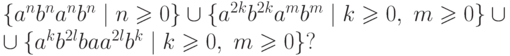
Упражнение 9.1.16. Какому классу принадлежит язык, порождаемый грамматикой

Упражнение 9.1.17. Существуют ли такие контекстно-свободные языки 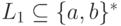 и
и 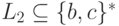 ,
что
язык
,
что
язык  не является контекстно-свободным?
не является контекстно-свободным?
