| Помогите решить задание лекции 3 курс Математическая теория формальных языков |
Неоднозначность в контекстно-свободных грамматиках
Перейдем к более богатому классу языков - к контекстно-свободным языкам. Они находят применение в разнообразных программных продуктах, таких как компиляторы, средства форматирования исходного кода, средства статического анализа программ, синтаксические редакторы, системы верстки, программы просмотра форматированного текста, поисковые системы.
Начнем рассмотрение контекстно-свободных языков с введения понятия деревьев вывода, что позволит определить важное для компьютерных приложений понятие однозначности контекстно-свободной грамматики. Чтобы не вдаваться в детали определения изоморфизма ориентированных деревьев, будем использовать в определении однозначности понятие левостороннего вывода (раздел 7.2). Соответствие деревьев вывода и левосторонних (а также правосторонних) выводов понадобится также в "лекции 13" .
Из класса всех контекстно-свободных языков можно выделить подкласс тех языков, для которых существует хотя бы одна однозначная грамматика. В разделе 7.3* доказывается, что все праволинейные (то есть автоматные) языки принадлежат этому подклассу.
В последнем разделе этой лекции приводятся важные конкретные примеры однозначных контекстно-свободных грамматик, моделирующих системы правильно вложенных скобок и польскую (префиксную) запись выражений.
7.1. Деревья вывода
Определение 7.1.1.
Выводам в контекстно-свободной грамматике
соответствуют так называемые деревья вывода
( деревья разбора,
derivation tree, parse tree) -
некоторые упорядоченные деревья, вершины которых помечены символами
алфавита  .
Корень дерева отвечает начальному символу.
Каждому символу слова w1,
на которое заменяется начальный символ на первом шаге вывода,
ставится в соответствие вершина дерева,
и к ней проводится дуга из корня.
Полученные таким образом непосредственные потомки корня
упорядочены согласно порядку их меток в слове w1.
Для тех из полученных вершин,
которые помечены символами из множества N,
делается аналогичное построение, и т. д.
.
Корень дерева отвечает начальному символу.
Каждому символу слова w1,
на которое заменяется начальный символ на первом шаге вывода,
ставится в соответствие вершина дерева,
и к ней проводится дуга из корня.
Полученные таким образом непосредственные потомки корня
упорядочены согласно порядку их меток в слове w1.
Для тех из полученных вершин,
которые помечены символами из множества N,
делается аналогичное построение, и т. д.
Кроной
(yield) дерева вывода называется слово, записанное в вершинах,
помеченных символами из алфавита  .
.
Пример 7.1.2. Рассмотрим контекстно-свободную грамматику
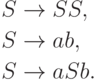
 соответствует следующее дерево вывода.
соответствует следующее дерево вывода.![\xymatrix @=6pt {
& & & & & & & S \ar[dllll]\ar[drr] \\
& & & S \ar[dll]\ar[drr] & & & & & & S \ar[dl]\ar[dr] \\
& S \ar[dl]\ar[dr] & & & & S \ar[dl]\ar[dr] & & & a & & b \\
a & & b & & a & & b
}](/sites/default/files/tex_cache/8b47e318f5b02a620d4f4c827adef444.png)
Упражнение 7.1.3. Перечислить все деревья вывода в грамматике
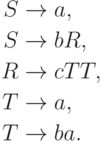
Упражнение 7.1.4. Существует ли праволинейная грамматика без  -правил, в которой
некоторое слово имеет бесконечно много выводов?
-правил, в которой
некоторое слово имеет бесконечно много выводов?
