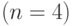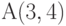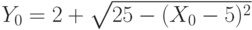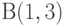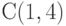| Почему область решений была взята как многоугольник ОАВС. А как же точки (567;0) и (0;320). На мой взгляд, я бы выбрал многоугольник с точками О (567;0) (0;320). Ведь они являются областью пересечения двух ограничений |
Графический метод оптимизации линейных моделей
Задача 1.3. Нелинейная задача
При застройке нового микрорайона требуется определить месторасположение нового торгового центра. Для обеспечения удобства всех жителей микрорайона необходимо так расположить торговый центр, чтобы суммарное расстояние переходов от него до жилых массивов было бы минимальным, а расстояние от каждого жилого массива до торгового центра не превышало бы 5. Координаты жилых массивов приведены в таблице 1.
| Координаты жилых массивов | ||
|---|---|---|
| X | Y | |
| Жилой массив 1 | 2 | 8 |
| Жилой массив 2 | 10 | 9 |
| Жилой массив 3 | 5 | 2 |
| Жилой массив 4 | 11 | 9 |
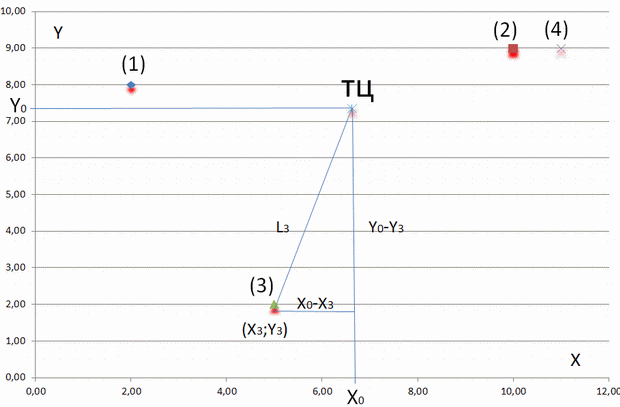
На рисунок 1.4 представлена наглядная схема расположения жилых массивов (1), (2), (3), (4).
Между ними должен быть размещен торговый центр ТЦ с координатами 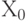 ,
, 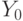 .
.
На рисунке показано, как вычисляют расстояния  между жилым массивом (3) и торговым центром:
между жилым массивом (3) и торговым центром:
 является гипотенузой треугольника с катетами
является гипотенузой треугольника с катетами  и
и  .
Аналогичным образом определяются и другие расстояния.
.
Аналогичным образом определяются и другие расстояния.
Математическая модель приведена в таблице:
Построим прямоугольную систему координат, где по оси 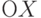 отложим значения
отложим значения  , а по оси
, а по оси  отложим значения
отложим значения
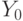 .
Значения
.
Значения  и
и  неотрицательны, поэтому можно ограничиться рассмотрением первого квадранта. Из условий задачи и
рисунка 1.4
следует, что
неотрицательны, поэтому можно ограничиться рассмотрением первого квадранта. Из условий задачи и
рисунка 1.4
следует, что  находится в интервале 2 – 11, а
находится в интервале 2 – 11, а 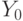 не выходит из интервала 2 – 9.
не выходит из интервала 2 – 9.
Из формулы расстояния между жилым массивом  и торговым центром выразим явным образом зависимость
и торговым центром выразим явным образом зависимость 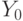 от
от  :
:
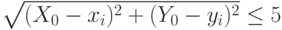
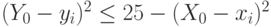

Знак + перед корнем берется для 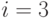 , в остальных случаях выбираем знак (-).
, в остальных случаях выбираем знак (-).
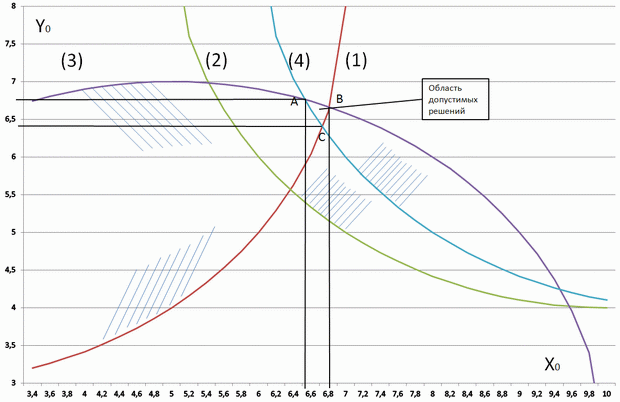
По последней формуле построим графики зависимости координат торгового центра от координат жилых массивов (1), (2), (3), (4). Они показаны на рисунок 1.5.
Каждая из кривых делит координатную плоскость на две части. Одна часть расположена выше прямой, вторая ниже. Чтобы найти ту полуплоскость, которая соответствует неравенствам, необходимо взять любую точку, принадлежащую одной из полуплоскостей (например, точку 7,4) и подставить ее координаты в неравенство. Если неравенство будет верным, то данная полуплоскость является искомой. Эти полуплоскости выделены штриховкой у каждой кривой.
Областью допустимых решений является замкнутый криволинейный треугольник 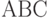 . Координаты торгового центра, выбранные в этом треугольнике,
удовлетворяют заданным неравенствам. Оптимальное решение следует искать в одной из вершин треугольника. Решая совместно уравнения кривых,
получим следующие результаты:
. Координаты торгового центра, выбранные в этом треугольнике,
удовлетворяют заданным неравенствам. Оптимальное решение следует искать в одной из вершин треугольника. Решая совместно уравнения кривых,
получим следующие результаты:


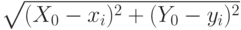
 ,
,  — координаты жилых
массивов
— координаты жилых
массивов 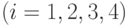
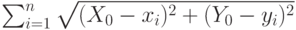
 — количество жилых массивов
— количество жилых массивов