|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Алгоритмы нечеткой оптимизации
Нечеткий вариант стандартной задачи математического программирования
получается,
если "смягчить" ограничения, т.е. допустить возможность
их нарушения с той или иной степенью. Кроме того, вместо максимизации целевой
функции  можно стремиться к достижению некоторого заданного
ее значения,
причем различным отклонениям значения
можно стремиться к достижению некоторого заданного
ее значения,
причем различным отклонениям значения  от этой величины
приписывать
различные степени допустимости (например, чем больше отклонение, тем меньше
степень его допустимости).
от этой величины
приписывать
различные степени допустимости (например, чем больше отклонение, тем меньше
степень его допустимости).
Пусть  — заданная величина функции цели
— заданная величина функции цели  , достижение которой считается
достаточным для выполнения цели принятия решений, и пусть имеется пороговый
уровень
, достижение которой считается
достаточным для выполнения цели принятия решений, и пусть имеется пороговый
уровень  , такой, что неравенство
, такой, что неравенство  означает
сильное нарушение
неравенства
означает
сильное нарушение
неравенства 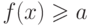 . Тогда функцию принадлежности для нечеткой
функции
цели можно определить следующим образом:
. Тогда функцию принадлежности для нечеткой
функции
цели можно определить следующим образом:
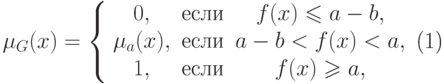 |
( 3) |
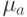 — функция принадлежности, описывающая степени
выполнения
соответствующего неравенства с точки зрения лица, принимающего решения.
— функция принадлежности, описывающая степени
выполнения
соответствующего неравенства с точки зрения лица, принимающего решения.Аналогично определяется функция принадлежности 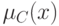 для
нечетких
ограничений. В результате исходная задача оказывается сформулированной в форме
задачи выполнения нечетко определенной цели, к которой применим подход
Беллмана-Заде (2).
для
нечетких
ограничений. В результате исходная задача оказывается сформулированной в форме
задачи выполнения нечетко определенной цели, к которой применим подход
Беллмана-Заде (2).
При моделировании ситуации в форме задачи линейного программирования
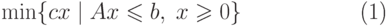 |
( 4) |
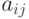 ,
,  и
и 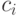 известно лишь то, что они
находятся в некотором множестве, отражающем все реальные возможности.
известно лишь то, что они
находятся в некотором множестве, отражающем все реальные возможности.В отдельных случаях точное описанное множество ограничений (допустимых альтернатив) может оказаться лишь приближением реальности в том смысле, что в реальной задаче альтернативы вне множества ограничений могут быть не допустимыми, а лишь в той или иной степени менее желательными для лица, принимающего решения, чем альтернативы внутри этого множества.
Рассмотрим задачу нахождения минимума на заданной области. Пусть задана область вида
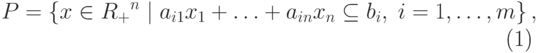 |
( 5) |
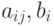 — нечеткие подмножества множества
— нечеткие подмножества множества  , а бинарная операция
, а бинарная операция 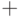 обозначает сложение нечетких множеств.
Требуется найти
обозначает сложение нечетких множеств.
Требуется найти 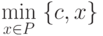 на заданной
области.
на заданной
области.Коэффициент при каждой переменной в ограничениях можно считать функцией полезности, определенной на числовой оси. Можно полагать, что эти коэффициенты дают субъективную оценку различных возможностей, включая, таким образом, другие не определенные ограничения.
Сведем решение исходной задачи к решению ряда задач линейного
программирования. Для этого введем дискретные  -уровни. В
результате
нечеткие ограничения принимают следующий интервальный вид:
-уровни. В
результате
нечеткие ограничения принимают следующий интервальный вид:
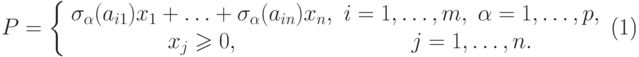 |
( 6) |
Таким образом, мы перешли от нечетких множеств к четко определенным и
теперь,
зная, что  — обычный интервал, можем записать нашу
задачу в следующем виде:
— обычный интервал, можем записать нашу
задачу в следующем виде:
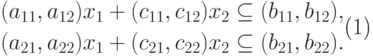 |
( 7) |
Теперь, чтобы привести задачу к виду обычной задачи линейного программирования, нам достаточно записать неравенства отдельно по левому и правому краям интервалов, с учетом знаков неравенства. Т.е., мы приведем систему к следующему виду:
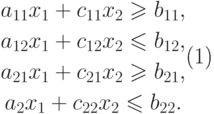 |
( 8) |
С помощью несложных преобразований мы перешли от задачи с нечеткими коэффициентами к задаче линейного программирования с четкими коэффициентами; при этом количество ограничений увеличилось в два раза и полученную задачу мы можем решить симплексным методом.
Таким образом, из рассмотренного примера явно просматривается алгоритм решения задачи с нечеткими коэффициентами. Следуя ходу рассуждений в данном примере, составим такой алгоритм. Он имеет следующий вид:
- Исходная задача.
- Вводим дискретные
 -уровни.
-уровни. - Ограничения принимают интервальный вид.
- Записываем неравенства отдельно по левому и правому краям с учетом знаков неравенства (при этом размерность увеличивается).
- Получаем задачу ЛП с четкими коэффициентами.
- Решаем полученную задачу симплекс-методом.
Как видим, исходная задача нечеткого математического
программирования
представляется в виде совокупности обычных задач линейного программирования
на всевозможных множествах уровня множества допустимых альтернатив.
Если альтернатива  есть решение
задачи
есть решение
задачи 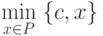 на множестве
уровня
на множестве
уровня  , то можно считать, что число
, то можно считать, что число  есть степень
принадлежности альтернативы
есть степень
принадлежности альтернативы  нечеткому множеству решений
исходной задачи.
нечеткому множеству решений
исходной задачи.
Перебрав, таким образом, всевозможные значения  ,
получаем функцию
принадлежности нечеткого решения.
,
получаем функцию
принадлежности нечеткого решения.
Если же и компоненты целевой функции 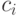 являются нечеткими,
то необходимо
выбирать для каждого уровня
являются нечеткими,
то необходимо
выбирать для каждого уровня  соответствующие границы
множеств
соответствующие границы
множеств 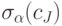 ,
, 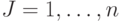 в соответствии с правилами интервальной арифметики,
минимизируя
предварительно таким образом:
в соответствии с правилами интервальной арифметики,
минимизируя
предварительно таким образом: 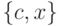 .
.
Из данного примера видно, что за гибкость приходится платить ценой увеличения размерности задачи. Фактически, исходная задача с ограничениями по включению преобразуется в задачу с ограничениями в виде неравенств, с которыми легко обращаться; при этом такая цена не слишком высока, поскольку сохраняется возможность использования хорошо разработанных классических методов.
